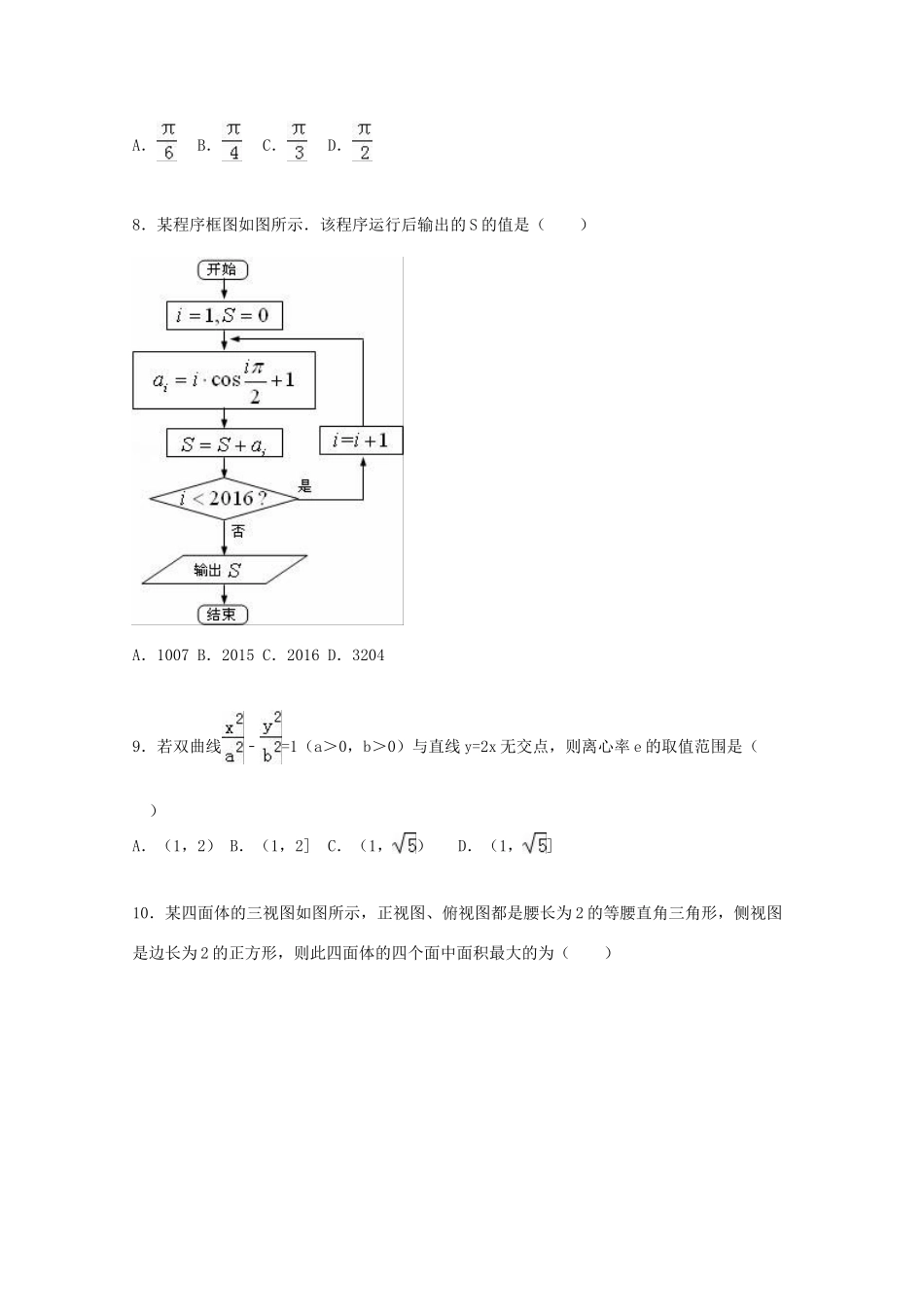
2016年广东省惠州市高考数学三调试卷(理科)一.选择题:本大题共12小题,每小题5分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={5,a2﹣3a+5},N={1,3},若M∩N≠∅,则实数a的值为()A.1B.2C.4D.1或22.复数z=+i3(i为虚数单位)的共轭复数为()A.1+2iB.i﹣1C.1﹣iD.1﹣2i3.若函数y=f(x)的定义域是,则函数g(x)=的定义域是()A.B.C.4.已知sinθ+cosθ=,,则sinθ﹣cosθ的值为()A.B.﹣C.D.﹣5.已知圆O:x2+y2=4上到直线l:x+y=a的距离等于1的点至少有2个,则a的取值范围为()A.(﹣3,3)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣2,2)D.6.甲、乙等5人在9月3号参加了纪念抗日战争胜利70周年阅兵庆典后,在天安门广场排成一排拍照留念,甲和乙必须相邻的排法有()种.A.24B.48C.72D.1207.已知向量=(sinA,)与向量=(3,sinA+cosA)共线,其中A是△ABC的内角,则角A的大小为()A.B.C.D.8.某程序框图如图所示.该程序运行后输出的S的值是()A.1007B.2015C.2016D.32049.若双曲线﹣=1(a>0,b>0)与直线y=2x无交点,则离心率e的取值范围是()A.(1,2)B.(1,2]C.(1,)D.(1,]10.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为()A.2B.4C.2D.211.设x,y满足条件,若目标函数z=ax+by(a>0,b>0)的最大值为12,则的最小值为()A.B.C.D.412.若函数f(x)满足:在定义域D内存在实数x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)为“1的饱和函数”.给出下列四个函数:①f(x)=;②f(x)=2x;③f(x)=lg(x2+2);④f(x)=cos(πx).其中是“1的饱和函数”的所有函数的序号为()A.①③B.②④C.①②D.③④二.填空题:本大题共4小题,每小题5分.13.已知a=﹣2sinxdx,则二项式(x2+)5的展开式中x的系数为.14.已知向量=(1,),=(3,m).若向量在方向上的投影为3,则实数m=.15.设数列{an}的n项和为Sn,且a1=a2=1,{nSn+(n+2)an}为等差数列,则{an}的通项公式an=.16.设点P在曲线y=ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为.三.解答题:解答应写出文字说明,证明过程或演算步骤.17.如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=(1)求△ACD的面积;(2)若BC=2,求AB的长.18.某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.(Ⅰ)求这4位乘客中至少有一名乘客在第2层下电梯的概率;(Ⅱ)用X表示4名乘客在第4层下电梯的人数,求X的分布列和数学期望.19.如图,已知四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(1)证明:AE⊥平面PAD;(2)取AB=2,若H为PD上的动点,EH与平面PAD所成最大角的正切值为,求二面角E﹣AF﹣C的余弦值.20.已知中心在原点的椭圆C:+=1的一个焦点为F1(0,3),M(x,4)(x>0)为椭圆C上一点,△MOF1的面积为.(1)求椭圆C的方程;(2)是否存在平行于OM的直线l,使得直线l与椭圆C相交于A,B两点,且以线段AB为直径的圆恰好经过原点?若存在,求出直线l的方程;若不存在,说明理由.21.已知函数f(x)=ax+x2﹣xlna(a>0,a≠1).(Ⅰ)求函数f(x)单调区间;(Ⅱ)若存在x1,x2∈,使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.【选修4-1:几何证明选讲】请考生在第22、23、24题中任选一题作答.答题时请写清题号并将相应信息点涂黑.22.如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.(Ⅰ)求证:|AE|=|EB|;(Ⅱ)求|EF|•|FC|的值.选修4-4:坐标系与参数方程23.已知曲线C的参数方程是(θ为参数),直线l的极坐标方程为ρsin(θ+)=.(其中坐标系满足极坐标原点与直角坐标系原点重合,极轴与直角坐标系x轴正半轴重合,单位长度相同.)(Ⅰ)将曲线C的参数方程化为普通方程...