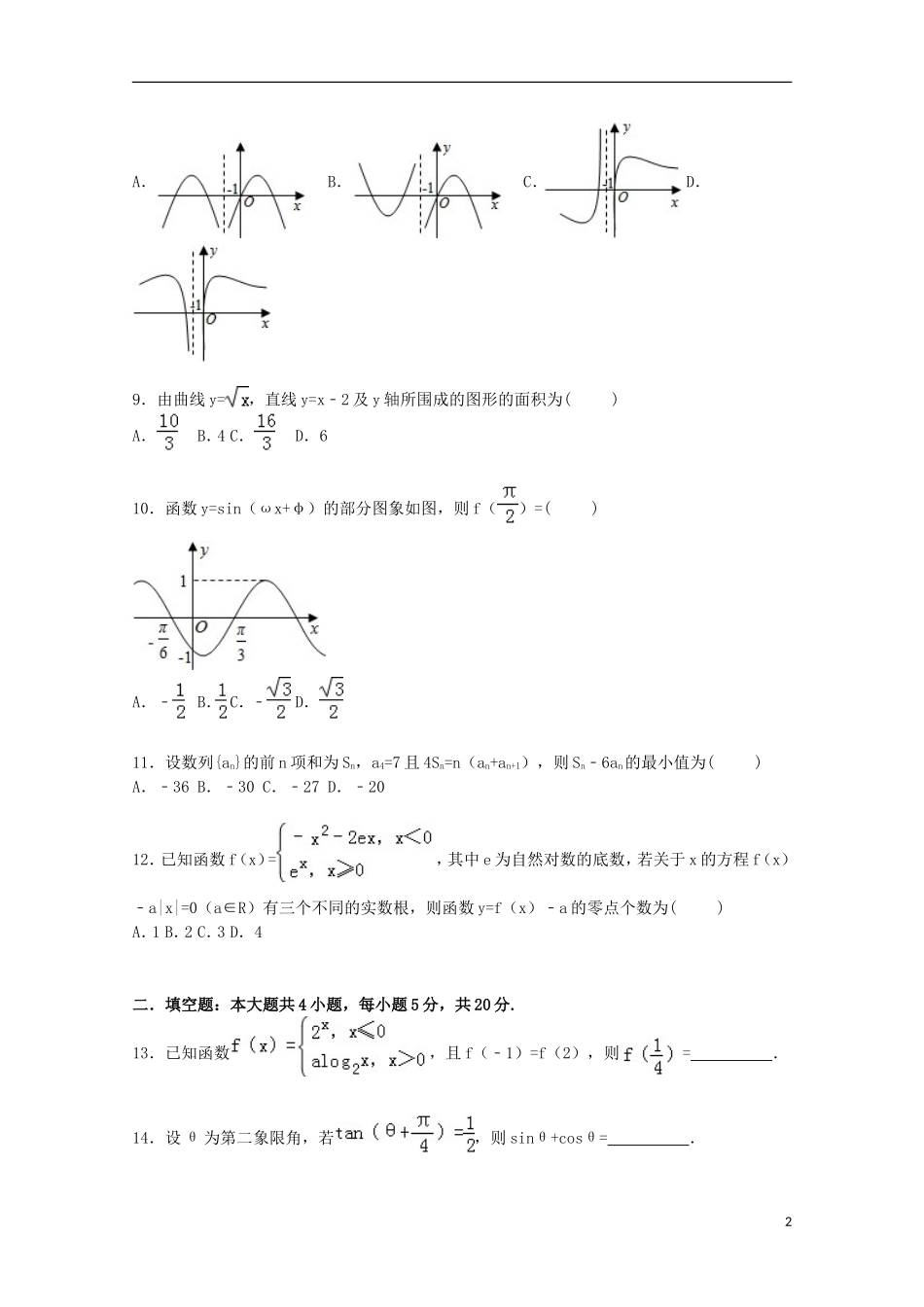
2015-2016学年湖南省张家界一中高三(上)第三次月考数学试卷(理科)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z=(i是虚数单位),则|z|=()A.1B.C.D.22.已知集合A={x|x2﹣x﹣2≤0},B={y|y=2x},则A∩B=()A.(0,2].B.(0,1].C.(﹣1,0]D.(0,4]3.已知命题p:∀x∈(0,+∞),x2≥x﹣1,则命题p的否定形式是()A.¬p:∃x0∈(0,+∞),x02≥x0﹣1B.¬p:∃x0∈(﹣∞,+0),x02≥x0﹣1C.¬p:∃x0∈(0,+∞),x02<x0﹣1D.¬p:∃x0∈(﹣∞,+0),x02<x0﹣14.设a为正实数,则“a≥1”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.为了得到的图象,只需将g(x)=2sinx的图象()A.纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移个单位B.纵坐标不变,横坐标伸长为原来的3倍,再将所得图象向右平移个单位C.纵坐标不变,横坐标缩短为原来的,再将所得图象向右平移个单位D.纵坐标不变,横坐标缩短为原来的,再将所得图象向右平移个单位6.若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)﹣g(x)=ex,则有()A.f(2)<f(3)<g(0)B.g(0)<f(3)<f(2)C.f(2)<g(0)<f(3)D.g(0)<f(2)<f(3)7.已知变量x,y满足约束条件,则的取值范围是()A.B.C.(﹣∞,3]∪[6,+∞)D.[3,6]8.下列四个图中,函数y=的图象可能是()1A.B.C.D.9.由曲线y=,直线y=x﹣2及y轴所围成的图形的面积为()A.B.4C.D.610.函数y=sin(ωx+φ)的部分图象如图,则f()=()A.﹣B.C.﹣D.11.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则Sn﹣6an的最小值为()A.﹣36B.﹣30C.﹣27D.﹣2012.已知函数f(x)=,其中e为自然对数的底数,若关于x的方程f(x)﹣a|x|=0(a∈R)有三个不同的实数根,则函数y=f(x)﹣a的零点个数为()A.1B.2C.3D.4二.填空题:本大题共4小题,每小题5分,共20分.13.已知函数,且f(﹣1)=f(2),则=__________.14.设θ为第二象限角,若,则sinθ+cosθ=__________.215.设函数f(x)=﹣3x+7,g(x)=lg(ax2﹣4x+a),若∀x1∈R,∃x2∈R,使f(x1)=g(x2),则实数a的取值范围为__________.16.在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧上变动(如图所示),若=λ+μ,其中λ,μ∈R.则2λ﹣μ的取值范围是__________.三.解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.已知||=4,||=3,(2﹣3)•(2+)=61.(1)求与的夹角θ;(2)若,且=0,求t及||18.在△ABC中,角A,B,C的对边分别是a、b、c,已知向量=(cosA,cosB),=(a,2c﹣b),且∥.(Ⅰ)求角A的大小;(Ⅱ)若a=4,求△ABC面积的最大值.19.某工厂生产某种产品,每日的成本C(单位:万元)与日产量x(单位:吨)满足函数关系式C=3+x,每日的销售额S(单位:万元)与日产量x的函数关系式S=,已知每日的利润L=S﹣C,且当x=2时,L=3.(1)求k的值;(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.20.已知二次函数y=f(x)的图象经过坐标原点,其导函数为f′(x)=6x﹣2.数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.(1)求数列{an}的通项公式;3(2)设,Tn是数列{bn}的前n项和,求使得对所有的(n∈N*)都成立的最小正整数m.21.已知数列{an}中,a1=1,an+1=(n∈N*)(1)求证:{}是等比数列,并求{an}的通项公式an;(2)数列{bn}满足bn=(3n﹣1)•,数列{bn}的前n项和为Tn,若不等式(﹣1)对一切n∈N*恒成立,求λ的取值范围.22.已知函数f(x)=lnx﹣x+1,x∈(0,+∞),g(x)=x3﹣ax.(1)求f(x)的最大值;(2)若对∀x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,求a的取值范围;(3)证明不等式:()n+()n+…+()n<.42015-2016学年湖南省张家界一中高三(上)第三次月考数学试卷(理科)...