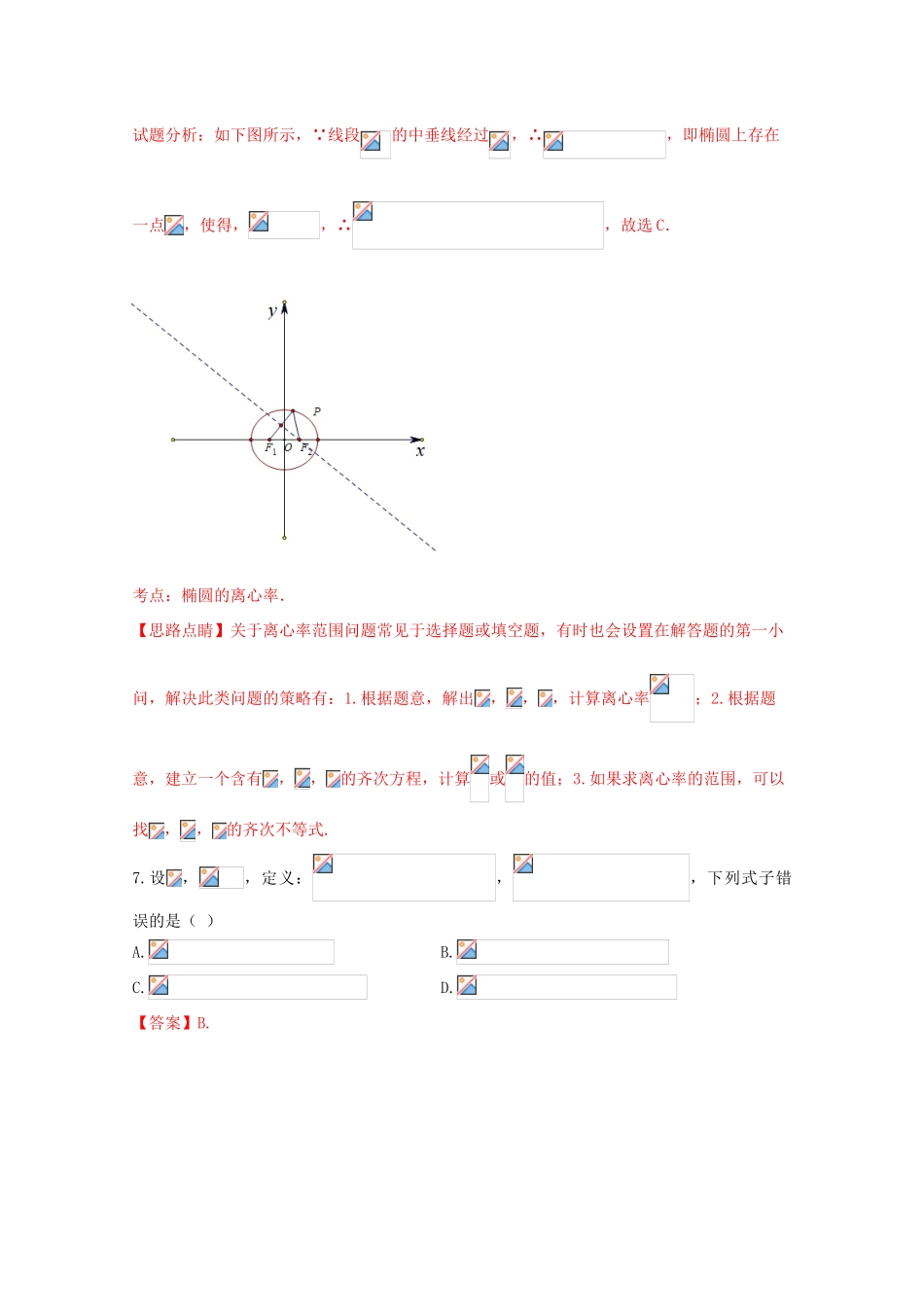
浙江省金丽衢十二校2016届高三数学上学期第一次联考试卷文(含解析)一、选择题(本大题共8个小题,每小题35分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列函数中,既不是奇函数,也不是偶函数的是()A.B.C.D.【答案】C.考点:函数的奇偶性判定.2.已知等差数列的前项和为,若,则()A.5B.C.15D.20【答案】C.【解析】试题分析: 等差数列,∴,故选C.考点:1.等差数列的前项和;2.等差数列的性质.3.已知,是两条不同的直线,是一个平面,则下列命题正确的是()A.若,,则B.若,,则C.若,,则D.若,,则【答案】D.【解析】试题分析:A:与的可能的位置关系有相交、异面、平行,故A错误;B:根据线面垂直的判定可知B错误;C:或,故C错误;D:根据线面垂直的性质可知D正确,故选D.考点:1.线面平行的判定与性质;2.线面垂直的判定与性质.4.设两直线:与:,则“”是“”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【答案】A.【解析】试题分析:若,则或,经检验,当时,与重合,∴,故是充分不必要条件,故选A.考点:1.两直线的位置关系;2.充分必要条件.5.若函数在区间上的最小值为6,则实数的值为()A.2B.C.1D.【答案】B.考点:基本不等式求最值.6.已知,分别是椭圆C:()的左、右焦点,若椭圆C上存在点,使得线段的中垂线恰好经过焦点,则椭圆C离心率的取值范围是()A.B.C.D.【答案】C.【解析】试题分析:如下图所示, 线段的中垂线经过,∴,即椭圆上存在一点,使得,,∴,故选C.考点:椭圆的离心率.【思路点睛】关于离心率范围问题常见于选择题或填空题,有时也会设置在解答题的第一小问,解决此类问题的策略有:1.根据题意,解出,,,计算离心率;2.根据题意,建立一个含有,,的齐次方程,计算或的值;3.如果求离心率的范围,可以找,,的齐次不等式.7.设,,定义:,,下列式子错误的是()A.B.C.D.【答案】B.考点:函数型新定义问题.【思路点睛】本题是一个新定义问题,定义了两个新的函数,但其本质还是一个关于某一个字母的分段函数,在判断每个选项时,应根据每一段的解析式分别求解,但要注意检验所求自变量的值或范围是否符合相应段的自变量的取值范围.8.在中,角A,B,C所对的边分别为,,,,,且为此三角形的内心,则()A.4B.5C.6D.7【答案】C.考点:1.三角形内心性质;2.平面向量数量积.【思路点睛】平面向量的综合题常与角度与长度结合在一起考查,在解题时运用向量的运算,数量积的几何意义,同时,需注意挖掘题目中尤其是几何图形中的隐含条件,常利用数形结合思想将问题等价转化为利用几何图形中的不等关系将问题简化,一般会与函数,不等式等几个知识点交汇,或利用平面向量的数量积解决其他数学问题是今后考试命题的趋势.二、填空题(本大题共7个小题,多空题每题6分,单空题每题4分,共36分.把答案填在题中的横线上.)9.已知全集,集合,,则,.【答案】,.【解析】试题分析: ,,∴,.考点:集合的运算.10.若双曲线的一个焦点为,则,该双曲线的渐近线方程为.【答案】,.【解析】试题分析:由题意得,,故双曲线方程为,渐近线方程为.考点:1.双曲线的标准方程;2.双曲线的渐近线.11.设函数,则,函数的零点为.【答案】,.考点:1.分段函数;2.分类讨论的数学思想.12.某几何体的三视图如图所示(单位:cm),则该几何体的体积是,表面积为.【答案】,.考点:1.三视图;2.空间几何体的体积与表面积.13.在中,角,,所对的边分别为,,,为边上的高,已知,,,则的值为.【答案】.【解析】试题分析: ,即,即,根据余弦定理,有,即,即,∴.考点:正余弦定理解三角形.14.设,实数,满足,若,则实数的最小值是.【答案】.【解析】试题分析:如下图所示,画出不等式组所表示的区域,由题意可知,不等式组所表示的区域应为所表示的平面区域的子集,从而可知.考点:线性规划的运用.【思路点睛】线性规则问题是高考的重点,而线性规划问题具有代数和几何的双重形式,多与函数、平面向量、数列、三角、概率、解析几何等问题交叉...