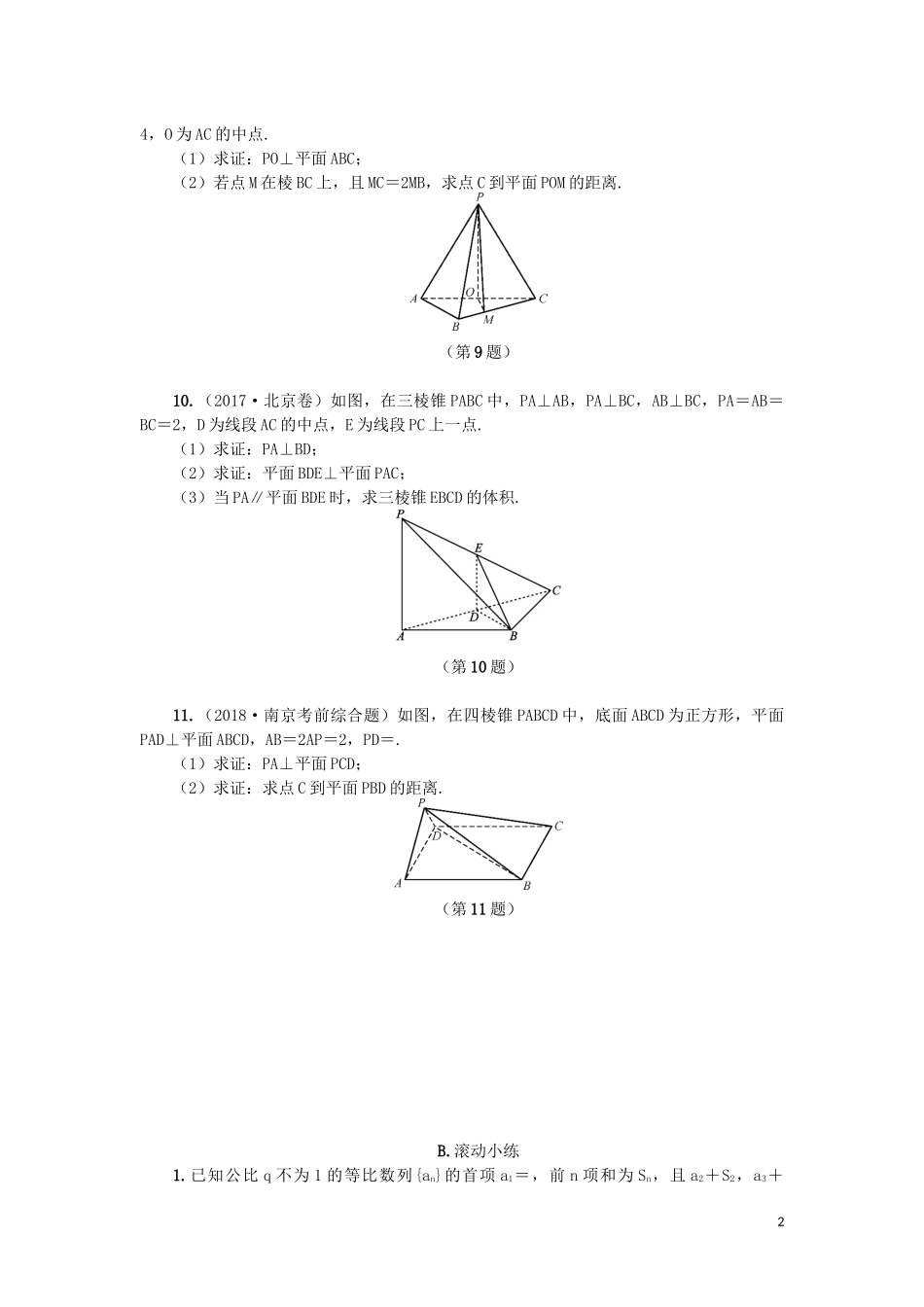
第49课空间几何体的表面积与体积A.课时精练一、填空题1.(2018·盐城中学)已知圆柱的底面半径为1,母线长与底面的直径相等,那么该圆柱的表面积为.2.(2017·苏北四市一模)将斜边长为4的等腰直角三角形绕其斜边所在直线旋转一周,则所形成的几何体的体积为.3.(2018·南通、泰州一调)如图,铜质六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知正六棱柱的底面边长、高都为4cm,圆柱的底面积为9cm2.若将该螺帽熔化后铸成一个高为6cm的正三棱柱零件,则该正三棱柱的底面边长为cm(不计损耗).(第3题)4.(2018·苏州大学指导卷Ⅱ)已知一个正方体外接球的体积为V1,内切球的体积为V2,那么的值为.5.(2018·常熟寒假调查)已知一个三棱锥的所有棱长均相等,且表面积为4,那么其体积为.6.(2018·江苏考前热身A卷)已知过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则该截面的面积S=.7.(2017·南京、盐城一模)将矩形ABCD绕边AB旋转一周得到一个圆柱,若AB=3,BC=2,圆柱上底面圆心为O,△EFG为下底面圆的一个内接直角三角形,则三棱锥OEFG体积的最大值是.8.(2018·扬州考前调研)若棱长都为1的正三棱锥的体积为V1,棱长都为1的正三棱柱的体积为V2,则=.二、解答题9.(2018·全国卷Ⅱ)如图,在三棱锥PABC中,已知AB=BC=2,PA=PB=PC=AC=14,O为AC的中点.(1)求证:PO⊥平面ABC;(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.(第9题)10.(2017·北京卷)如图,在三棱锥PABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥EBCD的体积.(第10题)11.(2018·南京考前综合题)如图,在四棱锥PABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,AB=2AP=2,PD=.(1)求证:PA⊥平面PCD;(2)求证:求点C到平面PBD的距离.(第11题)B.滚动小练1.已知公比q不为1的等比数列{an}的首项a1=,前n项和为Sn,且a2+S2,a3+2S3,a4+S4成等差数列,那么an+Sn=.2.(2017·南师大模拟)已知△ABC为锐角三角形,向量m=,n=(cosB,sinB),且m⊥n.(1)求角A-B的大小;(2)若cosB=,AC=8,求BC的长.34