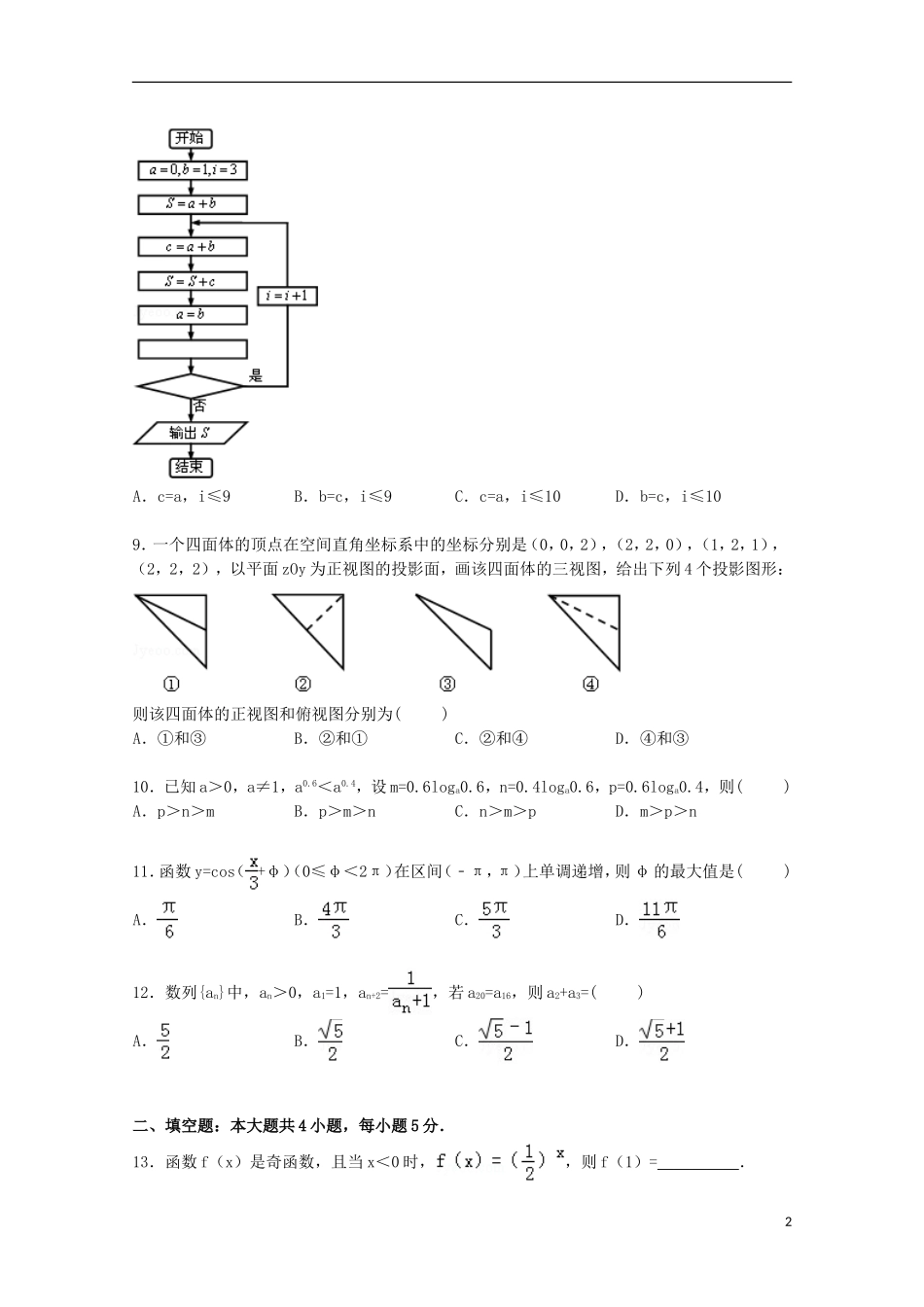
辽宁省丹东市2015届高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x>﹣1},A∪B=A,则集合B可以是()A.{0,2}B.{﹣1,0,1}C.{x|x≤0}D.R2.若复数为纯虚数,则实数m=()A.2B.﹣2C.D.3.命题“∀x≥0,|x|+x≥0”的否定是()A.∀x≥0,|x0|+x0<0B.∀x<0,|x|+x≥0C.∃x0≥0,|x0|+x0<0D.∃x0<0,|x|+x≥04.已知向量,满足•=0,||=1,||=2,则|+|=()A.B.2C.D.15.双曲线C:的渐近线方程为,则C的离心率为()A.B.C.D.6.设m,n是两条不同的直线,α,β是两个不同的平面,则()A.若m∥α,m∥β,则α∥βB.若m∥α,m∥n,则n∥αC.若m⊥α,m∥β,则α⊥βD.若m∥α,n⊂α,则m∥n7.若x,y满足,则下列不等式恒成立的是()A.y≥﹣1B.x≥2C.x+2y+2≥0D.2x﹣y+1≥08.斐波那契数列是:第1项是0,第2项是1,从第三项开始,每一项都等于前两项之和.某同学设计了一个求这个数列的前10项和的程序框图,那么在空白矩形框和判断框内应分别填入的语句是()1A.c=a,i≤9B.b=c,i≤9C.c=a,i≤10D.b=c,i≤109.一个四面体的顶点在空间直角坐标系中的坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),以平面zOy为正视图的投影面,画该四面体的三视图,给出下列4个投影图形:则该四面体的正视图和俯视图分别为()A.①和③B.②和①C.②和④D.④和③10.已知a>0,a≠1,a0.6<a0.4,设m=0.6loga0.6,n=0.4loga0.6,p=0.6loga0.4,则()A.p>n>mB.p>m>nC.n>m>pD.m>p>n11.函数y=cos(+φ)(0≤φ<2π)在区间(﹣π,π)上单调递增,则φ的最大值是()A.B.C.D.12.数列{an}中,an>0,a1=1,an+2=,若a20=a16,则a2+a3=()A.B.C.D.二、填空题:本大题共4小题,每小题5分.13.函数f(x)是奇函数,且当x<0时,,则f(1)=__________.214.设等差数列{an}的前n项和为Sn,若S8=4a3,a9=﹣6,则a7=__________.15.设M(x0,y0)为抛物线C:y2=8x上一点,F为C的焦点,若以F为圆心,|FM|为半径的圆和C的准线相交,则x0的取值范围是__________.16.已知函数f(x)=x,若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数,则使函数f(x)有极值点的概率为__________.三、解答题:解答应写出文字说明,证明过程或演算步骤.(一)必做题17.直角△ABC中,AB=4,BC=3,点D在斜边AC上,且AD=4DC.(Ⅰ)求BD的长;(Ⅱ)求sin∠CDB的值.18.2015届高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数x与答题正确率y%的关系,对某校2015届高三某班学生进行了关注统计,得到如下数据:x1234y20305060(Ⅰ)求y关于x的线性回归方程,并预测答题正确率是100%的强化训练次数;(Ⅱ)若用(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间21.设函数f(x)=ex+ax+b点(0,f(0))处的切线方程为x+y+1=0.(Ⅰ)求a,b值,并求f(x)的单调区间;(Ⅱ)证明:当x≥0时,f(x)>x2﹣4.(二)选做题(请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题计分.做答时请写清题号)【选修4-1:几何证明选讲】22.如图,AB是⊙O的直径,CB与⊙O相切于点B,E为线段BC上一点,连接AC,连接AE,分别交⊙O于D,G两点,连接DG交CB于点F.(Ⅰ)求证:C,D,E,G四点共圆.;(Ⅱ)若F为EB的三等分点且靠近E,GA=3GE,求证:CE=EB.3【选修4-4:坐标系与参数方程】23.长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动,=2,点P的轨迹为曲线C.(Ⅰ)以直线AB的倾斜角α为参数,写出曲线C的参数方程;(Ⅱ)求点P到点D(0,﹣1)距离d的取值范围.【选修4-5:不等式选讲】24.已知a>0,b>0.(I)若a+b=2,求的最小值;(Ⅱ)求证:a2b2+a2+b2≥ab(a+b+1).辽宁省丹东市2015届高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x>﹣1},...