江苏省高考数学第一轮复习第十五单元试卷 空间中有关角 苏教版VIP免费

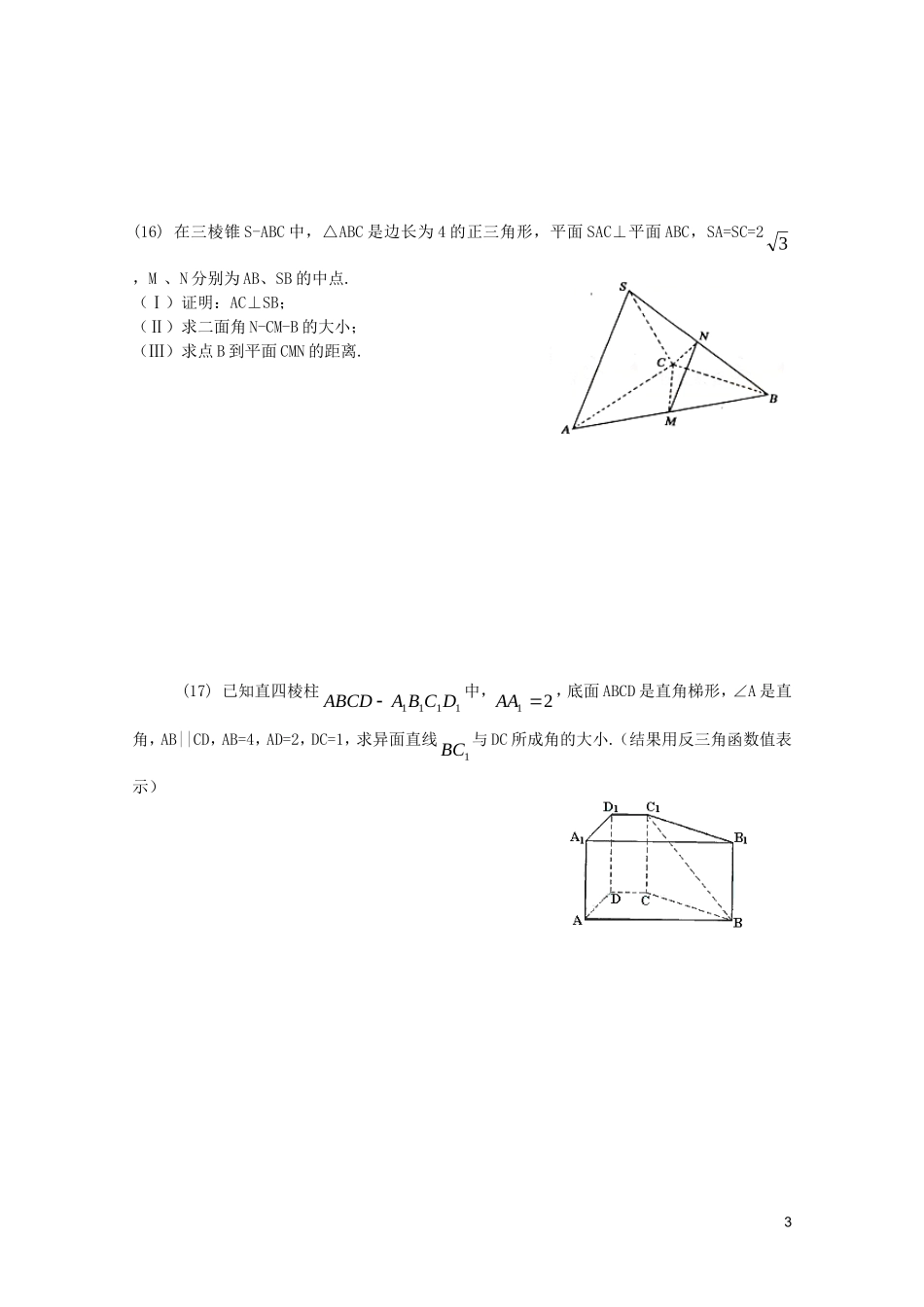
第十五单元空间中有关角、距离的计算一.选择题.(1)已知),1,2,1(),1,1,0(ba则a与b的夹角等于()A．90°B．30°C．60°D．150°(2)正方体ABCD－A1B1C1D1中,E、F分别是棱AB,BB1的中点,A1E与C1F所成的角是θ，则()A．θ=600B．θ=450C．52cosD．52sin(3)设A，B，C，D是空间不共面的四点，且满足0ACAB，0ADAC，0ADAB，则△BCD是()A．钝角三角形B．直角三角形C．锐角三角形D．不确定(4)如图，长方体ABCD—A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角是()A．515arccosB．4C．510arccosD．2(5)把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的三棱锥体积最大时，直线BD和平面ABC所成的角的大小为()A．90°B．60°C．45°D．30°(6)如图,在正方体ABCD－A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是()A．直线B．圆C．双曲线D．抛物线(7)在正三棱柱ABC-A1B1C1中,若AB=2BB1,则AB1与C1B所成角的大小为()A．60°B．90°C．105°D．75°(8)在正三棱柱ABC-A1B1C1中，若AB=2，AA1=1，则点A到平面A1BC的距离为()1A．43B．23C．433D．3(9)将B=600,边长为1的菱形ABCD沿对角线AC折成二面角,若[60°,120°],则折后两条对角线之间的距离的最值为()A．最小值为43,最大值为23B．最小值为43,最大值为43C．最小值为41,最大值为43D．最小值为43,最大值为23(10)如图，正方体ABCD－A1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则O到平面ABC1D1的距离为()A．21B．42C．22D．23二.填空题(11)直三棱柱ABC-A1B1C1中,∠A1B1C1=90°,且AB=BC=BB1,E,F分别是AB,CC1的中点,那么A1C与EF所成的角的余弦值为.(12)如图，在三棱锥P—ABC中，PA=PB=PC=BC，且2BAC，则PA与底面ABC所成角为..(13)如图，正方体的棱长为1，C、D分别是两条棱的中点，A、B、M是顶点，那么点M到截面ABCD的距离是.(14)已知平面α和平面β交于直线l，P是空间一点，PA⊥α，垂足为A，PB⊥β，垂足B，且PA=1，PB=2，若点A在β内的射影与点B在α内的射影重合，则点P到l的距离为.三.解答题(15)如图，正三角形ABC的边长为3，过其中心G作BC边的平行线，分别交AB、AC于1B、1C．将11CAB沿11CB折起到111CBA的位置，使点1A在平面CCBB11上的射影恰是线段BC的中点M．求：二面角MCBA111的大小2(16)在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=23，M、N分别为AB、SB的中点.（Ⅰ）证明：AC⊥SB；（Ⅱ）求二面角N-CM-B的大小；（Ⅲ）求点B到平面CMN的距离.(17)已知直四棱柱1111DCBAABCD中，21AA，底面ABCD是直角梯形，∠A是直角，AB||CD，AB=4，AD=2，DC=1，求异面直线1BC与DC所成角的大小.（结果用反三角函数值表示）3(18)如图3所示，在四面体P—ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=342.F是线段PB上一点，341715CF，点E在线段AB上，且EF⊥PB.（Ⅰ）证明：PB⊥平面CEF；（Ⅱ）求二面角B—CE—F的大小.4B参考答案一选择题:1.D[解析]：以D为原点建立坐标系23623||||cosbaba01502.C[解析]：)21,0,1()1,21,0(11FCEA52||||cos1111FCEAFCEA3.C[解析]：0))((22ABABADABABACADACABADABACBDBCB0||||cos故BDBCBDBCB是锐角同理,D,C都是锐角.故△BCD是锐角三角形.4.D[解析]：以D为原点建立坐标系)1,1,1(),1,0,1(1GFEA01GFEA异面直线A1E与GF所成的角是25.C[解析]：如图,当平面BAC平面DAC时,三棱锥体积最大取AC的中点E,则BE平面DAC,故直线BD和平面ABC所成的角为DBE5DEACBFcosDBE=22BDBE,∴DBE=4506.D[解析]： P到直线直线C1D1的距离就是P到C1的距离,∴点P到直线BC与点C1的距离相等故动点P的轨迹所在的曲线是以C1为焦点、以直线BC为准线的抛物线7.B[解析]：以A为原点建立坐标系，AC，AA1为y,z轴，垂直于平面AA1C1C直线为x轴，则)2,21,23(),2,21,23(11ACAB故1AB1AC=08.B[解析]：点A到平面A1BC的距离为h BCAAABCAVV11∴hSAASBCAABC131311∴h...