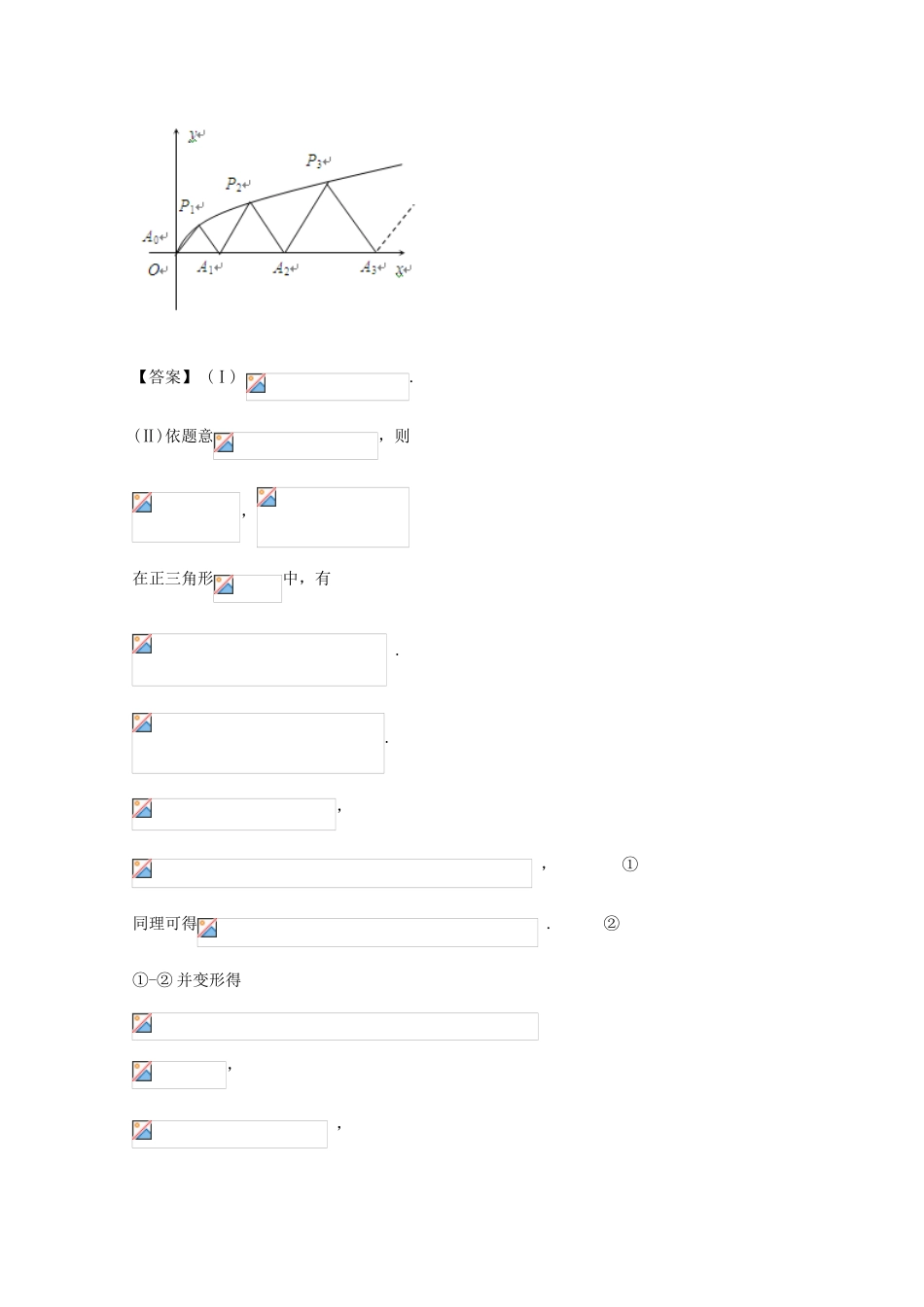
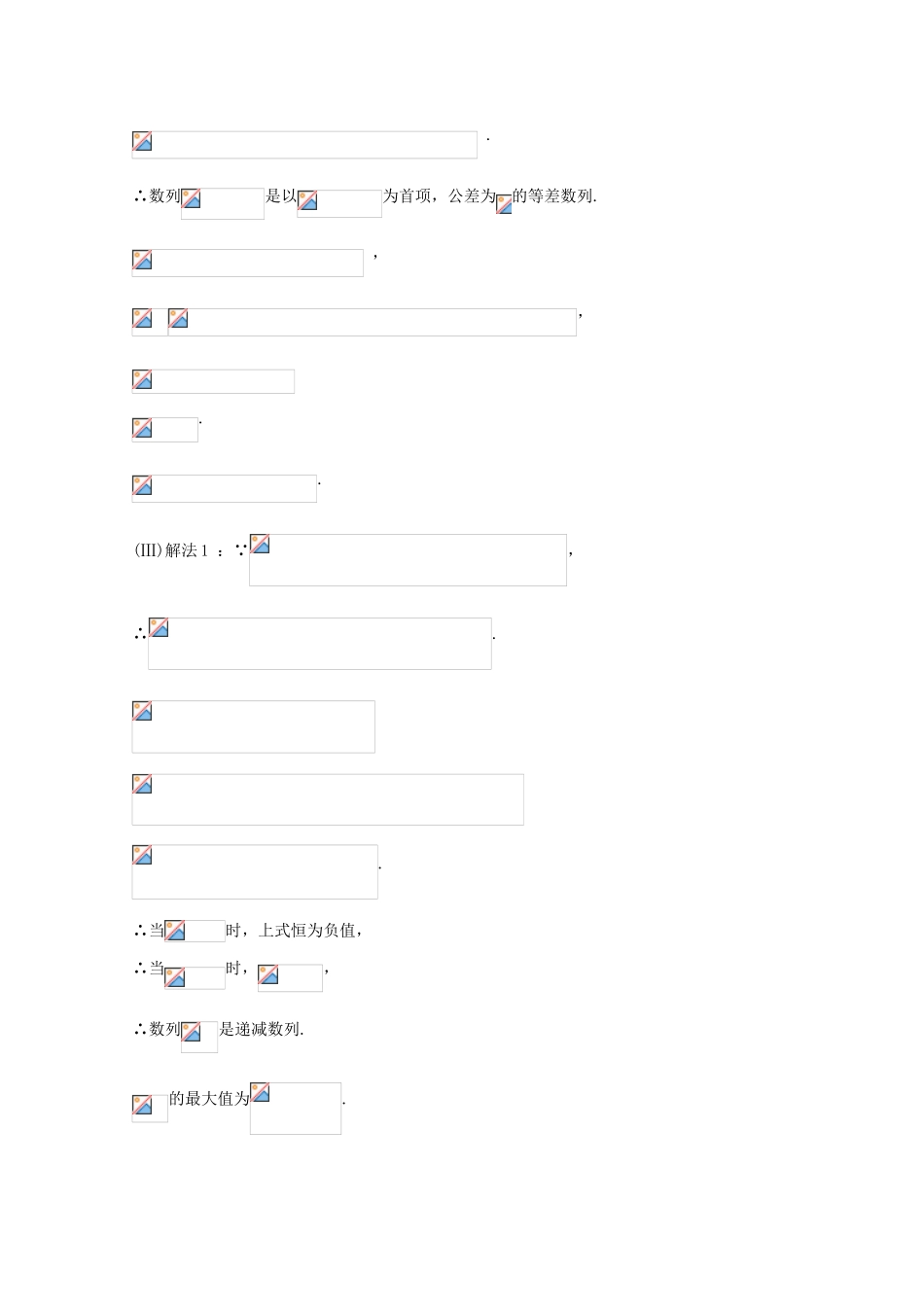
数列0219.如图,是曲线上的个点,点在轴的正半轴上,是正三角形(是坐标原点).(Ⅰ)写出;(Ⅱ)求出点的横坐标关于的表达式;(Ⅲ)设,若对任意正整数,当时,不等式恒成立,求实数的取值范围.【答案】(Ⅰ).(Ⅱ)依题意,则,在正三角形中,有..,,①同理可得.②①-②并变形得,,.∴数列是以为首项,公差为的等差数列.,,..(Ⅲ)解法1:∵,∴..∴当时,上式恒为负值,∴当时,,∴数列是递减数列.的最大值为.若对任意正整数,当时,不等式恒成立,则不等式在时恒成立,即不等式在时恒成立.设,则且,∴解之,得或,即的取值范围是.20.在数列中,,。(Ⅰ)求的通项公式;(Ⅱ)令,求数列的前项和。(Ⅲ)求数列的前项和。【答案】(Ⅰ)由条件得,又时,,故数列构成首项为1,公式为的等比数列.从而,即.(Ⅱ)由得,,两式相减得:,所以.(Ⅲ)由得所以.21.设为数列的前项之积,满足.(1)设,证明数列是等差数列,并求和;(2)设求证:.【答案】(1)∵,∴∴,∵∴.∵∴,∴,∴,∴数列是以2为首项,以1为公差的等差数列,∴,∴,∴(2),∵∴当时,,当时,,∴.22.已知各项均为正数的两个数列和满足:,,(1)设,,求证:数列是等差数列;(2)设,,且是等比数列,求和的值.【答案】(1)∵,∴。∴。∴。∴数列是以1为公差的等差数列。(2)∵,∴。∴。(﹡)设等比数列的公比为,由知,下面用反证法证明若则,∴当时,,与(﹡)矛盾。若则,∴当时,,与(﹡)矛盾。∴综上所述,。∴,∴。又∵,∴是公比是的等比数列。若,则,于是。又由即,得。∴中至少有两项相同,与矛盾。∴。∴。∴。