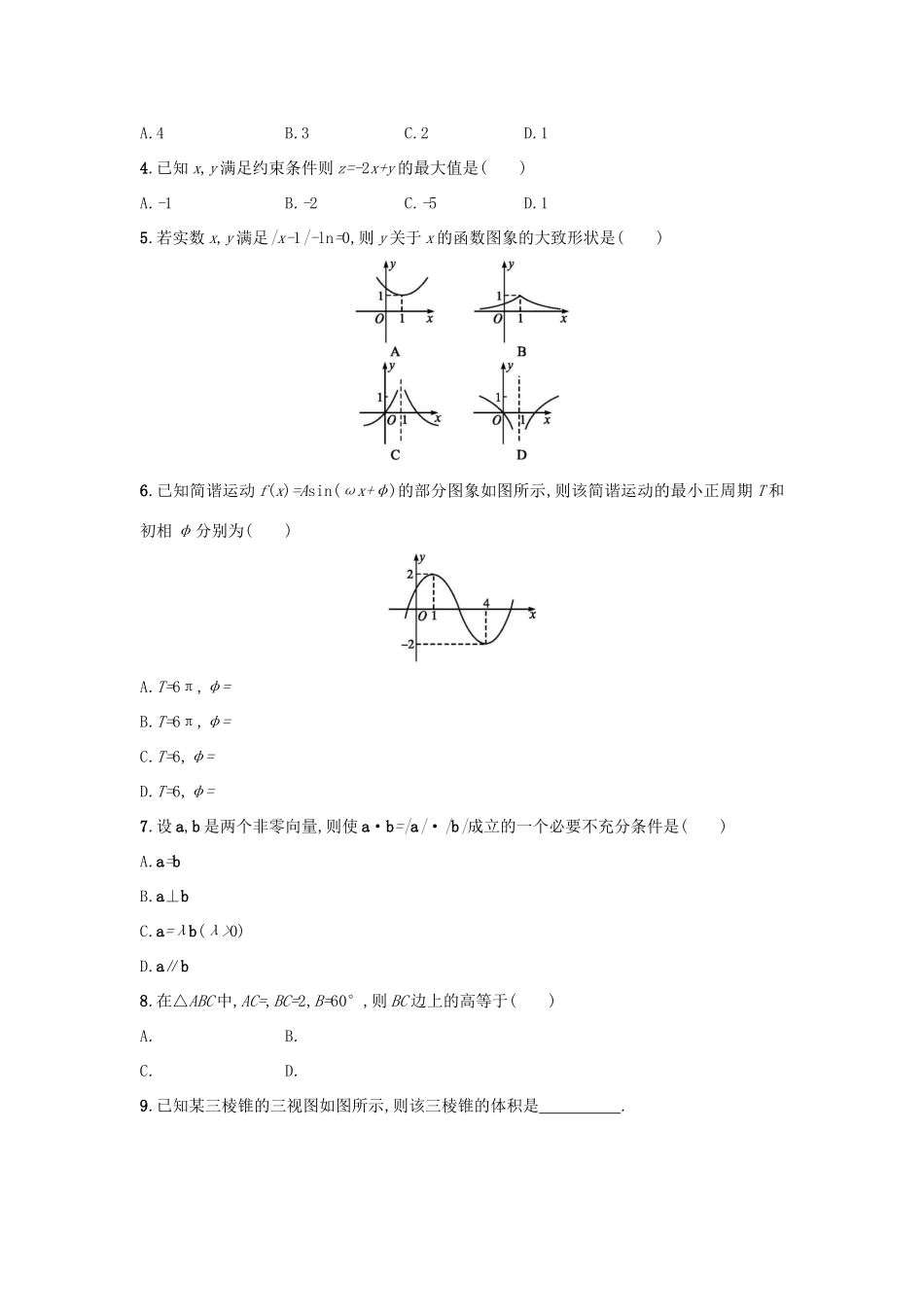
题型练2选择、填空综合练(二)能力突破训练1.设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是()A.6B.5C.4D.32.复数=()A.iB.1+iC.-iD.1-i3.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为()4.(2017天津河西区高三质量调查)若存在实数x,使|x-a|+|x-1|≤3成立,则实数a的取值范围是()A.[-2,1]B.[-2,2]C.[-2,3]D.[-2,4]5.已知p:∀x∈[-1,2],4x-2x+1+2-a<0恒成立,q:函数y=(a-2)x是增函数,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.下列四个命题中真命题的个数是()①“x=1”是“x2-3x+2=0”的充分不必要条件②命题“∀x∈R,sinx≤1”的否定是“∃x0∈R,sinx0>1”③“若am20},B=,则A∩B=()A.{x|x>-2}B.{x|x<3}C.{x|x<-2或x>3}D.{x|-20)D.a∥b8.在△ABC中,AC=,BC=2,B=60°,则BC边上的高等于()A.B.C.D.9.已知某三棱锥的三视图如图所示,则该三棱锥的体积是.10.(2017全国Ⅲ,文14)双曲线=1(a>0)的一条渐近线方程为y=x,则a=.11.(2017江苏,4)下图是一个算法流程图.若输入x的值为,则输出y的值是.12.已知平面向量a,b,|a|=1,|b|=2,a·b=1.若e为平面单位向量,则|a·e|+|b·e|的最大值是.13.已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为.14.设{an}是集合{2s+2t|0≤st2-2t+2对任意t∈恒成立.令y=t2-2t+2=(t-1)2+1,当t∈时,ymax=10,所以a>10.关于q:只需a-2>1,即a>3.故p是q的充分不必要条件.6.D解析由x=1,得x2-3x+2=0,反之,若x2-3x+2=0,则x=1或x=2,①是真命题;全称命题的否定是特称命题,②是真命题;原命题的逆命题为“若a