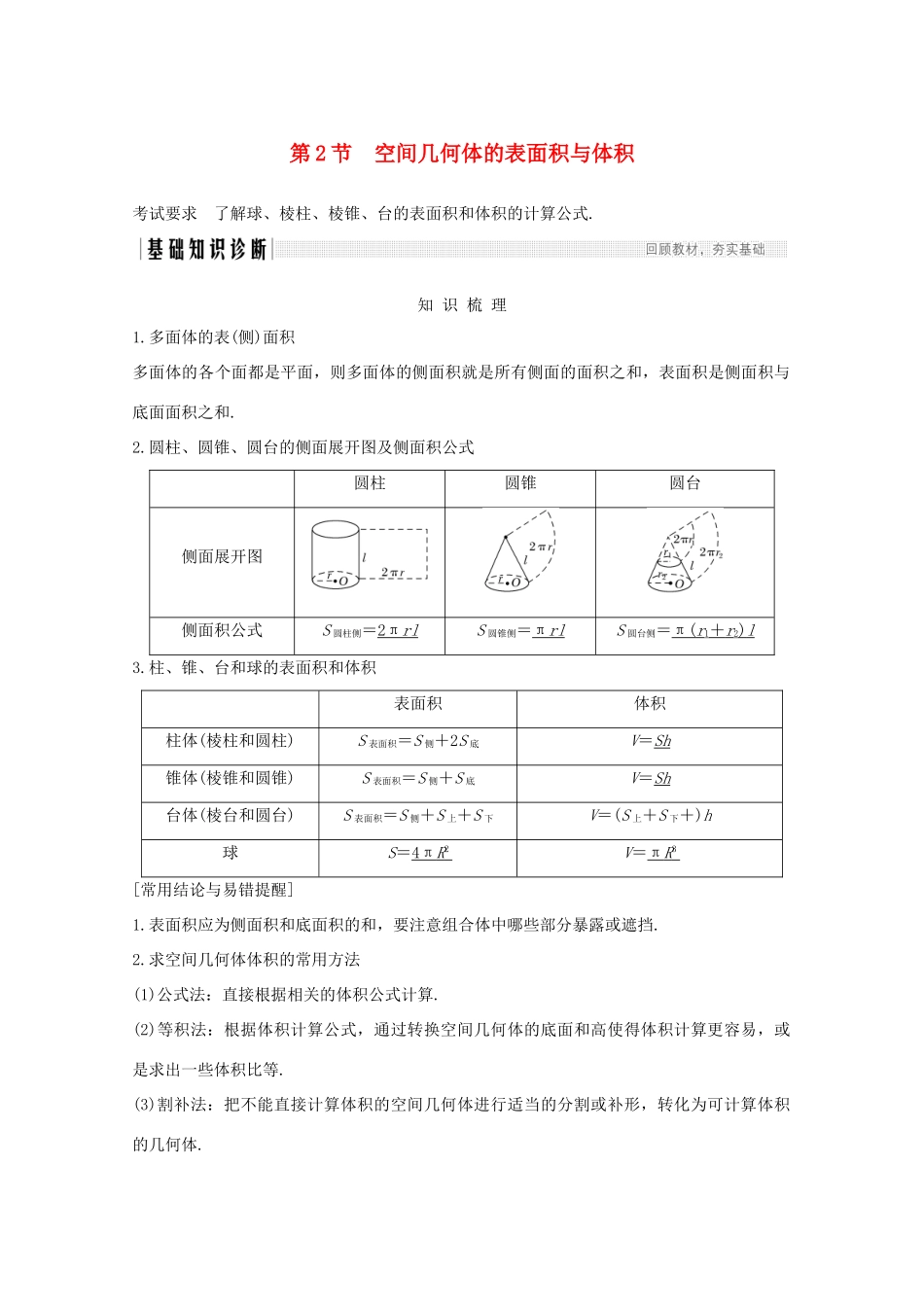
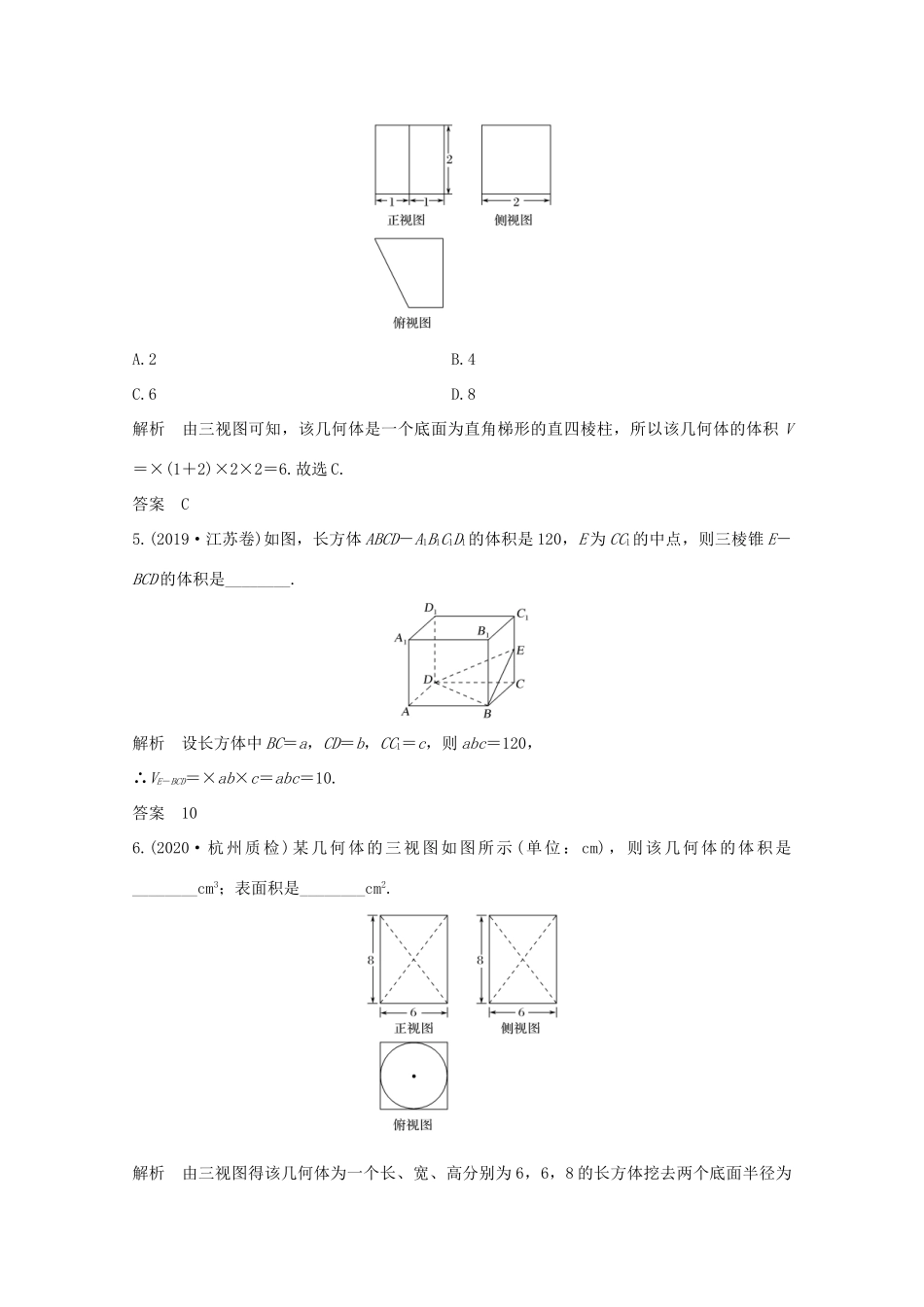
第2节空间几何体的表面积与体积考试要求了解球、棱柱、棱锥、台的表面积和体积的计算公式.知识梳理1.多面体的表(侧)面积多面体的各个面都是平面,则多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧=2πrlS圆锥侧=πrlS圆台侧=π(r1+r2)l3.柱、锥、台和球的表面积和体积表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=Sh锥体(棱锥和圆锥)S表面积=S侧+S底V=Sh台体(棱台和圆台)S表面积=S侧+S上+S下V=(S上+S下+)h球S=4πR2V=πR3[常用结论与易错提醒]1.表面积应为侧面积和底面积的和,要注意组合体中哪些部分暴露或遮挡.2.求空间几何体体积的常用方法(1)公式法:直接根据相关的体积公式计算.(2)等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.(3)割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.诊断自测1.判断下列说法的正误.(1)锥体的体积等于底面面积与高之积.()(2)球的体积之比等于半径比的平方.()(3)台体的体积可转化为两个锥体的体积之差.()(4)已知球O的半径为R,其内接正方体的边长为a,则R=a.()解析(1)锥体的体积等于底面面积与高之积的三分之一,故不正确.(2)球的体积之比等于半径比的立方,故不正确.答案(1)×(2)×(3)√(4)√2.已知圆锥的表面积等于12πcm2,其侧面展开图是一个半圆,则底面圆的半径为()A.1cmB.2cmC.3cmD.cm解析S表=πr2+πrl=πr2+πr·2r=3πr2=12π,∴r2=4,∴r=2(cm).答案B3.(2020·北京通州期末)某四棱锥的三视图如图所示,在此四棱锥的侧面中面积最小的侧面面积为()A.1B.C.2D.解析由三视图画出该四棱锥的直观图,如图所示:在此四棱锥P-ABCD的四个侧面中,面积最小的侧面是Rt△PBC,它的面积为BC·PB=×1×=.答案B4.(2018·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.2B.4C.6D.8解析由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V=×(1+2)×2×2=6.故选C.答案C5.(2019·江苏卷)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是________.解析设长方体中BC=a,CD=b,CC1=c,则abc=120,∴VE-BCD=×ab×c=abc=10.答案106.(2020·杭州质检)某几何体的三视图如图所示(单位:cm),则该几何体的体积是________cm3;表面积是________cm2.解析由三视图得该几何体为一个长、宽、高分别为6,6,8的长方体挖去两个底面半径为3,高为4的圆锥体后剩余的部分,则其体积为6×6×8-2××4×π×32=288-24π,表面积为2(6×6+6×8+6×8)-2×π×32+2××5×2×π×3=264+12π.答案288-24π264+12π考点一空间几何体的表面积【例1】(1)(2020·温州适应性测试)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是()A.8cm2B.12cm2C.(4+2)cm2D.(4+4)cm2(2)(2020·浙江新高考仿真卷五)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.8解析(1)由视图得该几何体是底面为边长为2的正方形,高为2的正四棱锥,则其侧面的高为=,所以该几何体的表面积为2×2+4××2×=4+4,故选D.(2)由三视图得该几何体为一个半球和一个半圆柱的组合体,且半圆柱的底面和半球体的一半底面重合,则其表面积为×4πr2+πr2+2r×2r+×2πr×2r=4r2+5πr2=16+20π,解得r=2,故选B.答案(1)D(2)B规律方法空间几何体表面积的求法.(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.(3)旋转体的表面积问题注意其侧面展开图的应用.【训练1】(1)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是________.(2)(2020·浙江新高考仿真卷一)《九章算术》...