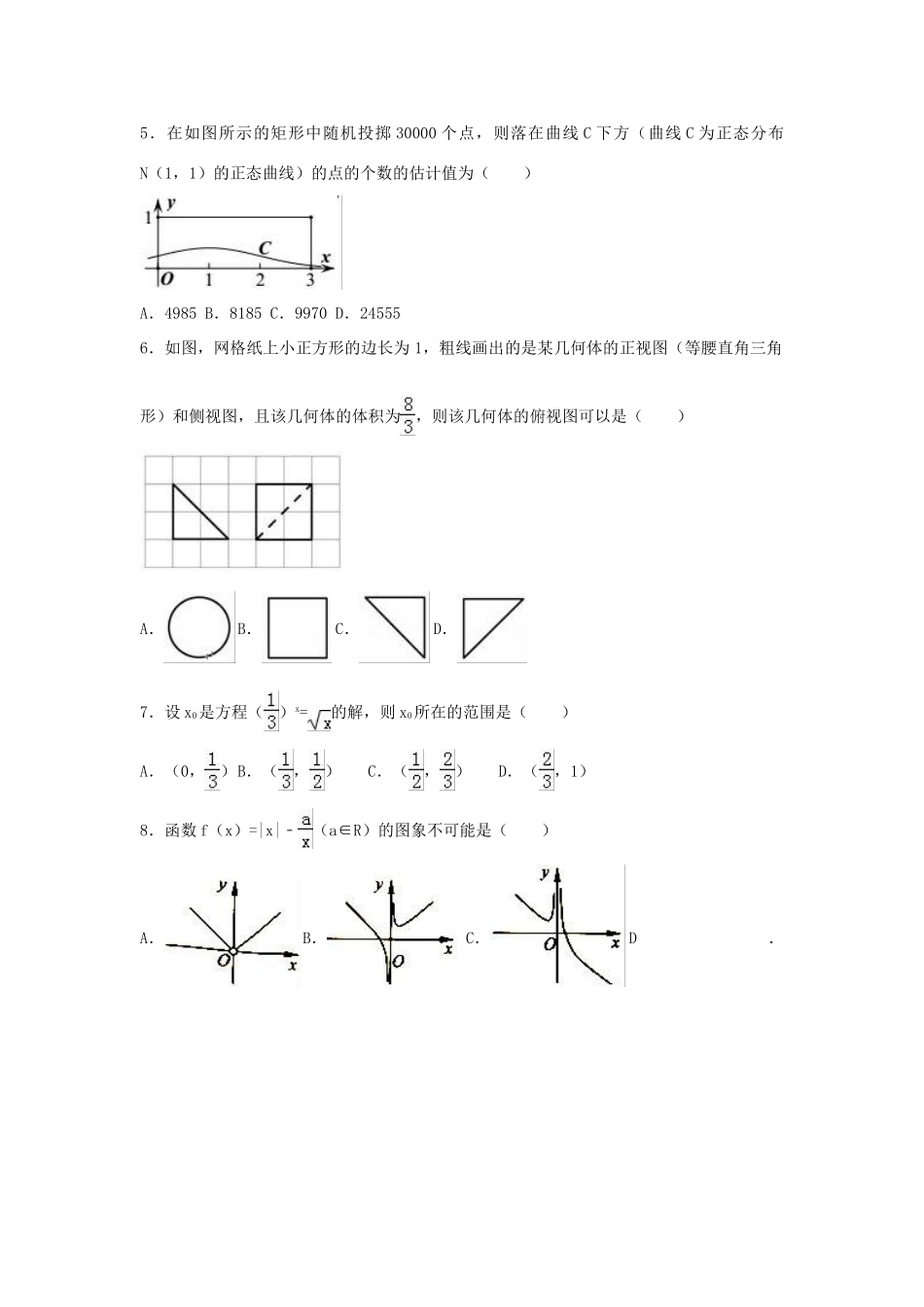
2017年湖南省衡阳市常宁市高考数学压轴试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.设复数z满足=1﹣i,则复数z在复平面内的对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限2.已知集合A={y|y=2cos2x﹣1},B={x|y=},则A∪B=()A.{x|﹣1≤x≤0}B.{x|0≤x<1}C.{x|﹣1<x<2}D.{x|﹣1≤x≤2}3.我国南宋时期的数学家秦九韶是普州(现四川省安岳县)人,秦九韶在其所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一例,则输出的S的值为()A.4B.﹣5C.14D.﹣234.下列选项中,错误的是()A.若p为真,则¬(¬p)也为真B.若“p∧q为真”,则“p∨q为真”为真命题C.∃x∈R,使得tanx=2017D.“2x>”是“logx<0”的充分不必要条件5.在如图所示的矩形中随机投掷30000个点,则落在曲线C下方(曲线C为正态分布N(1,1)的正态曲线)的点的个数的估计值为()A.4985B.8185C.9970D.245556.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的正视图(等腰直角三角形)和侧视图,且该几何体的体积为,则该几何体的俯视图可以是()A.B.C.D.7.设x0是方程()x=的解,则x0所在的范围是()A.(0,)B.(,)C.(,)D.(,1)8.函数f(x)=|x|﹣(a∈R)的图象不可能是()A.B.C.D.9.已知奇函数y=f(x),x∈R,a=[f(x)+x2]dx,则二项式(﹣)9的展开式的常数项为()A.﹣B.﹣C.﹣1D.﹣10.如图,圆锥的高PO=,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则点B到平面PAC的距离()A.B.C.D.111.已知A是双曲线﹣=1(a>0,b>0)的左顶点,F1,F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若=λ,||=,||+||=8,则双曲线的标准方程为()A.x2﹣=1B.﹣y2=1C.=1D.x2﹣=112.已知函数f(x)=的图象上有且仅有四个不同的点关于直线y=﹣1的对称点在y=kx﹣1的图象上,则实数k的取值范围是()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量=(1,2),=(x,﹣1),若∥(),则,的夹角为.14.若实数x,y满足约束条件,若a<恒成立,则a的取值范围为.15.已知抛物线y2=4x的焦点F,过焦点的直线与抛物线交于A,B两点,则4|FA|+|FB|的最小值为.16.已知锐角△ABC的外接圆O的半径为1,∠B=,则的取值范围为.三、解答题:本大题共5小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.设数列{an}是公差大于0的等差数列,Sn为数列{an}的前n项和,已知S3=9,且2a1,a3﹣1,a4+1构成等比数列.(1)求数列{an}的通项公式;(2)若数列{bn}满足=2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.18.某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图:(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:等级一等品二等品三等品重量(g)[5,25)[25,45)[45,55]按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.19.如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,(Ⅰ)求证:面ADE⊥面BDE;(Ⅱ)求直线AD与平面DCE所成角的正弦值..20.已知椭圆E:+=1(a>b>0)上点P,其左、右焦点分别为F1,F2,△PF1F2的面积的最大值为,且满足=3(1)求椭圆E的方程;(2)若A,B,C,D是椭圆上互不重合的四个点,AC与BD相交于F1,且•=0,求的取值范围.21.设函数f(x)=ex+sinx(e为自然对数的底数),g(x)=ax,F(x)=f(x)﹣g(x).(1)若x=0是F(x)的极值点,且直线x=t(t≥0)分别与函数f(x)和g(x)的图象交于P,Q,求P,Q两点间的最短距离;(2)若x≥0时,函数y=F(x)的图象恒在y=F(﹣x)...