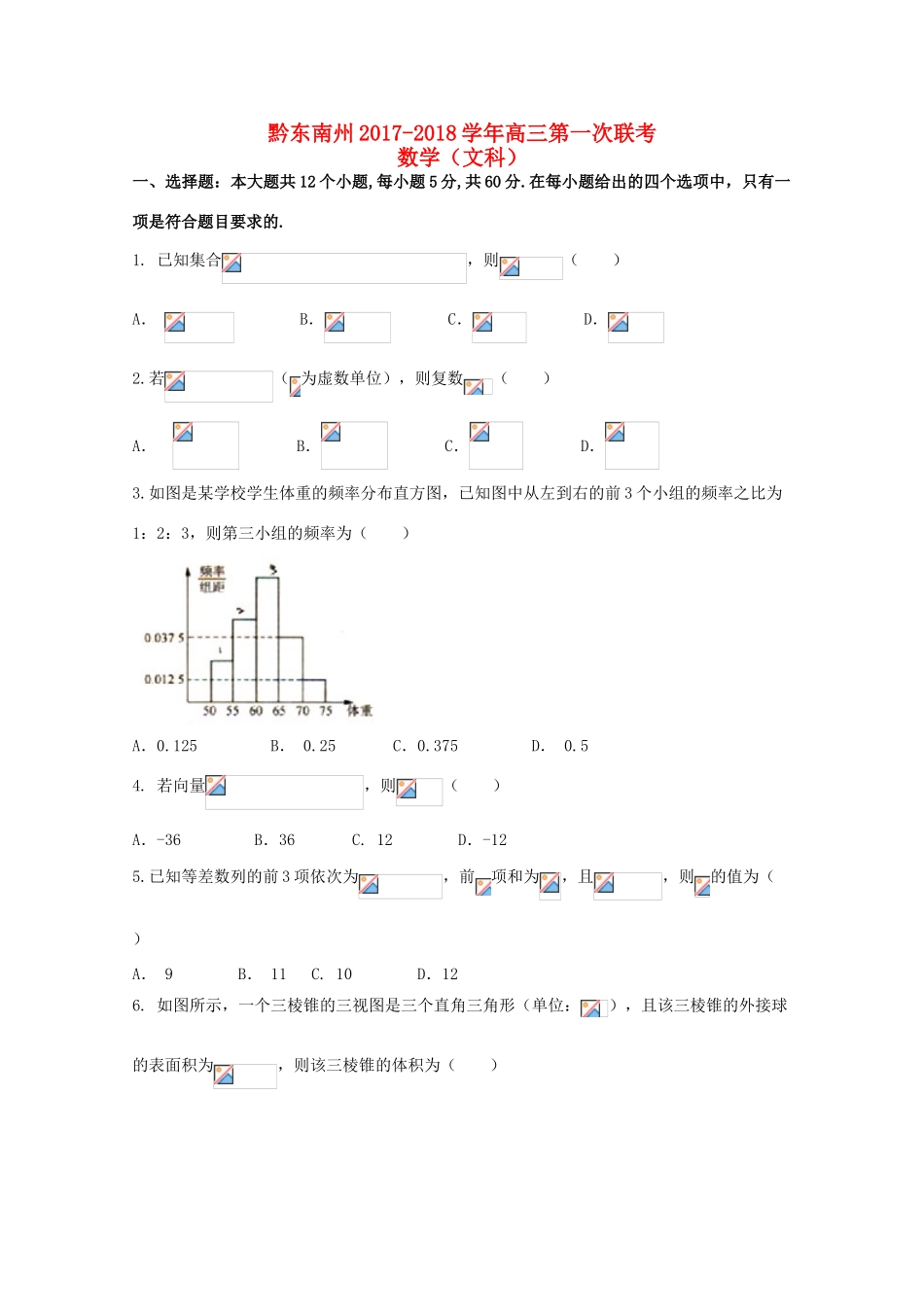
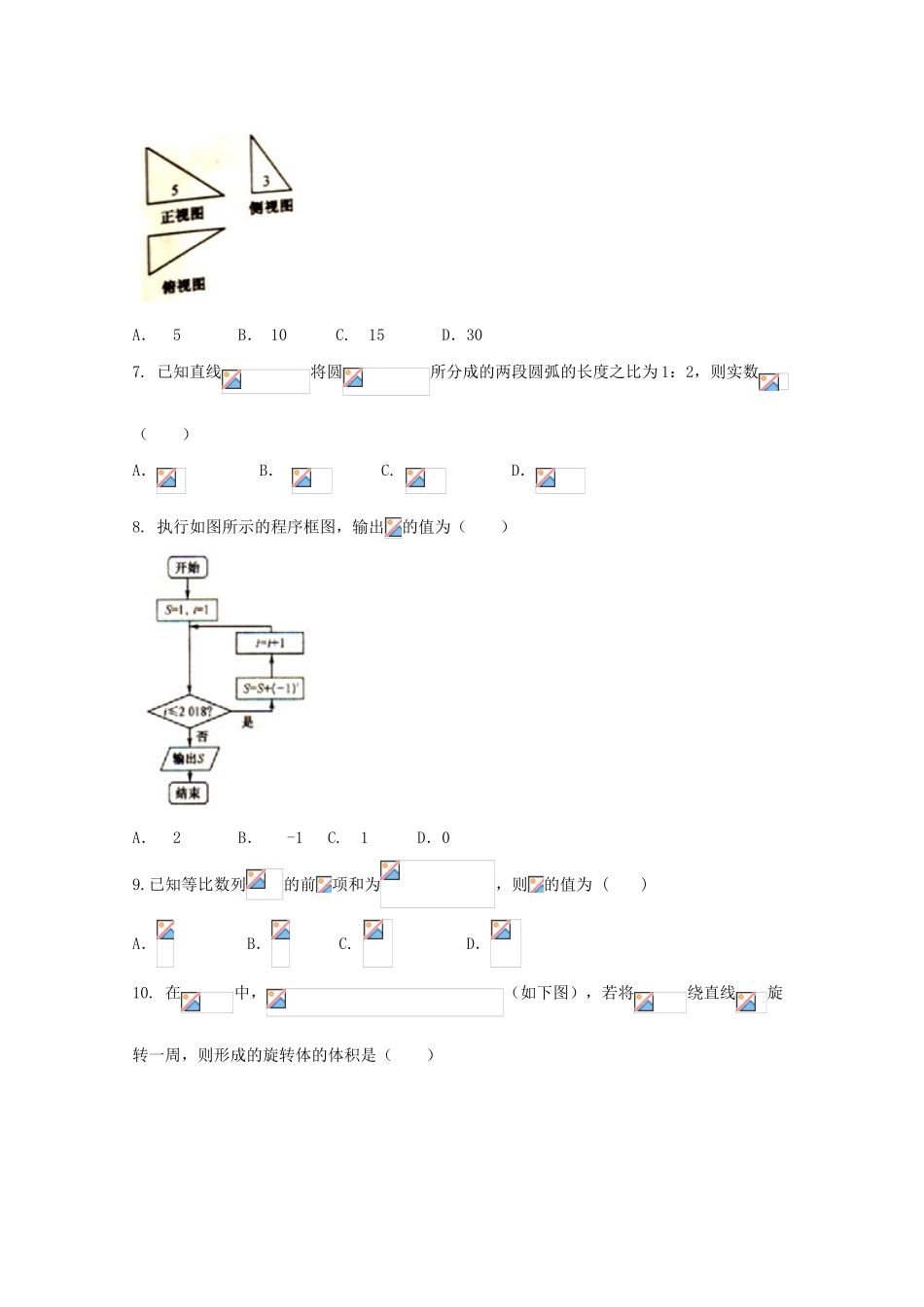
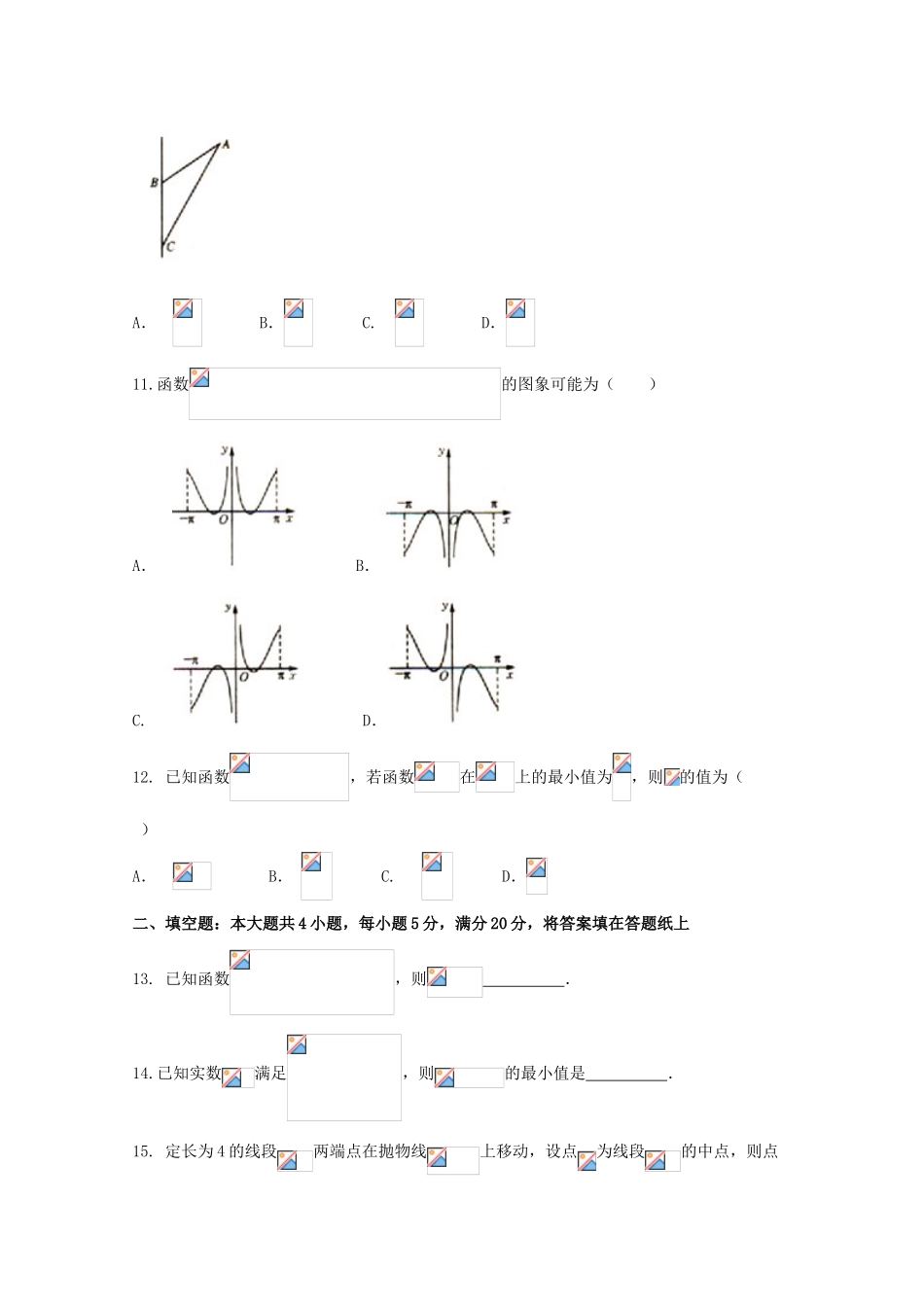
黔东南州2017-2018学年高三第一次联考数学(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,则()A.B.C.D.2.若(为虚数单位),则复数()A.B.C.D.3.如图是某学校学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,则第三小组的频率为()A.0.125B.0.25C.0.375D.0.54.若向量,则()A.-36B.36C.12D.-125.已知等差数列的前3项依次为,前项和为,且,则的值为()A.9B.11C.10D.126.如图所示,一个三棱锥的三视图是三个直角三角形(单位:),且该三棱锥的外接球的表面积为,则该三棱锥的体积为()A.5B.10C.15D.307.已知直线将圆所分成的两段圆弧的长度之比为1:2,则实数()A.B.C.D.8.执行如图所示的程序框图,输出的值为()A.2B.-1C.1D.09.已知等比数列的前项和为,则的值为()A.B.C.D.10.在中,(如下图),若将绕直线旋转一周,则形成的旋转体的体积是()A.B.C.D.11.函数的图象可能为()A.B.C.D.12.已知函数,若函数在上的最小值为,则的值为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,满分20分,将答案填在答题纸上13.已知函数,则.14.已知实数满足,则的最小值是.15.定长为4的线段两端点在抛物线上移动,设点为线段的中点,则点到轴距离的最小值为.16.若函数在上存在单调递增区间,则实数的取值范围为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.在中,角的对边分别为,且.(1)求的值;(2)若的周长为5,求的面积.18.经研究,城市公交车的数量太多容易造成资源浪费,太少又难以满足乘客需求.为此,某市公交公司从某站占的40名候车乘客中随机抽取15人,将他们的候车时间(单位:)作为样本分成5组如下表:组别侯车时间人数一2二6三2四2五3(1)估计这40名乘客中侯车时间不少于20分钟的人数;(2)若从上表侯车时间不少于10分钟的7人中选2人作进一步的问卷调查,求抽到的两人侯车时间都不少于20分钟的概率.19.如图,四棱锥中,底面是直角梯形,,是正三角形,是的中点.(1)求证:;(2)判定是否平行于平面,请说明理由.20.已知椭圆过点,椭圆的左焦点为,右焦点为,点是椭圆上位于轴上方的动点,且,直线与直线分别交于两点.(1)求椭圆的方程及线段的长度的最小值;(2)是椭圆上一点,当线段的长度取得最小值时,求的面积的最大值.21.设函数.(1)讨论函数的单调性;(2)若,求函数的最值.22.以平面直角坐标系的原点为极点,轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点的参数方程为(为参数),点在曲线上.(1)求在平面直角坐标系中点的轨迹方程和曲线的普通方程;(2)求的最大值.试卷答案一、选择题1-5:CBCDC6-10:BCCCD11、12:DA二、填空题13.414.015.16.三、解答题17.解:(1)由及正弦定理,得,又由余弦定理,得,故.(2)若的周长为5,又,所以.故的面积为.18.解:(1)侯车时间不少于20分钟的概率为,所以估计侯车时间不少于20分钟的人数为.(2)将侯车时间在范围的4名乘客编号为;侯车时间在范围的3名乘车编号为.从7人中任选两人包含以下21个基本事件:,其中抽到的两人侯车时间都不少于20分钟包含以下3个基本事件:,故所求概率为.19.(1)取的中点为,连接,由于是正三角形,所以,又易知四边形是平行四边形,所以,所以,平面平面,又,故平面,又平面,故.(2)解:平行于平面,理由如下:取的中点为,连接.可知,又,所以四边形为平行四边形,故.又平面平面,所以平面.20.解:(1)由,得,所以,又椭圆过点,所以,解得,故椭圆的方程为,设点,则由,得,即,则,由,得,所以线段的长度取得最小值.(2)由(1)可知,当的长度取得最小值时,,将点代入,得,故此时点,则直线的方程为,此时,当平行于的直线与椭圆下方相切时,的面积取最大值,设直线,则由,得,则,所以,或(舍去).由平行线间的距离公式,得此时点到直线的距离.故,即的面积的最大值为.21.解:(1),令,得,①若,则恒成立,所以函数在上单调递增...