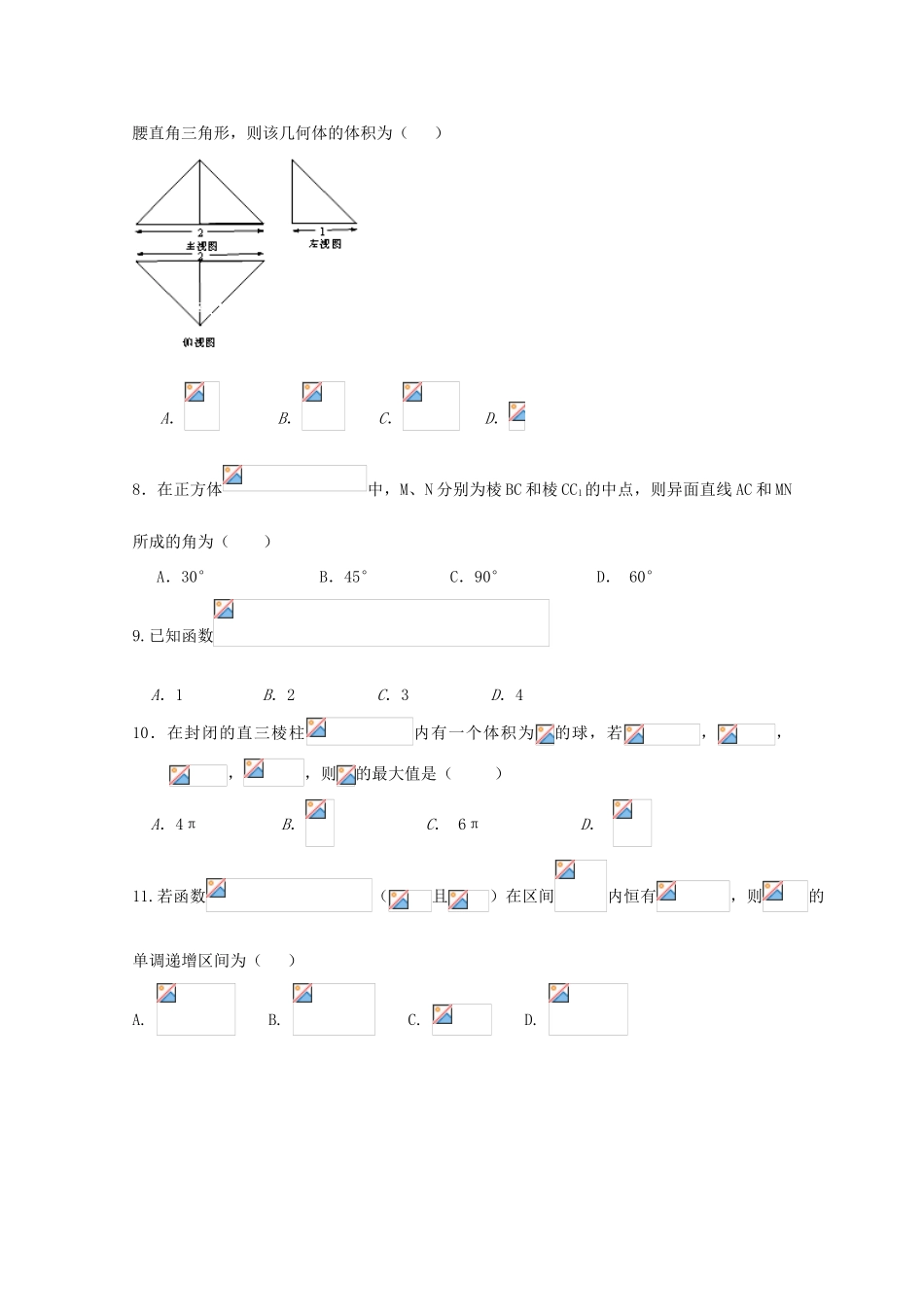
河南省林州市2017-2018学年高一数学12月调考试题(普通班)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,时间120分钟。第Ⅰ卷(选择题共60分)一、选择题:(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列说法正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点2.函数的定义域为()A.B.C.D.3.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()A.B.C.D.4.函数的零点所在的大致区间是()A.B.C.D.5.已知,则()A.B.C.D.6.已知直线a,b和平面α,β,给出以下命题,其中正确的是()A.若a∥β,α∥β,则a∥αB.若α∥β,a⊂α,则a∥βC.若α∥β,a⊂α,b⊂β,则a∥bD.若a∥β,b∥α,α∥β,则a∥b7.一个几何体的三视图及部分数据如图所示,正(主)视图、侧(左)视图和俯视图都是等腰直角三角形,则该几何体的体积为()A.B.C.D.8.在正方体中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为()A.30°B.45°C.90°D.60°9.已知函数A.1B.2C.3D.410.在封闭的直三棱柱内有一个体积为的球,若,,,,则的最大值是()A.4πB.C.6πD.11.若函数(且)在区间内恒有,则的单调递增区间为()A.B.C.D.12.设函数,若关于的方程有四个不同的解且,则的取值范围是()A.B.C.D.第Ⅱ卷(选择题90分)二、填空题(本大题共4小题每小题5分,计20分)13.设函数则____________14.空间四边形ABCD中,且AB与CD所成的角为,E、F分别是BC、AD的中点,则EF与AB所成角的大小为____________。15.据说阿基米德死后,敌军将领给他建了一块墓碑,在墓碑上刻了一个图案(如图),图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.图案中圆锥、球、圆柱的体积比为____________16.如图所示是一几何体的平面展开图,其中ABCD为正方形,E,F,分别为PA,PD的中点,在此几何体中,给出下面三个结论:①直线BE与直线CF异面;②直线BE与直线AF异面;③直线EF∥平面PBC;其中正确的有(填序号)____________。高一数学,共(4)页第1页三、解答题(本大题共6小题,计70分)17.(10分)如图,已知正方体ABCD-A1B1C1D1中,M是AA1的中点,N是BB1的中点.求证:平面MDB1∥平面ANC.18.(12分)已知集合,.(1)求;(2)若集合,且,求实数的取值范围.19.(本小题12分)已知正四棱锥P﹣ABCD如图所示.(Ⅰ)若其正视图是一个边长分别为、,2的等腰三角形,求其表面积S、体积V;(Ⅱ)设AB中点为M,PC中点为N,证明:MN∥平面PAD.20.(本题12分)已知函数.(1)当时,求函数的值域;(2)是否存在,使在上单调递增,若存在,求出的取值范围,不存在,请说明理由.21.(12分)如图所示,在三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的点.高一数学,共(4)页第4页若平面BC1D∥平面AB1D1,求的值.22.(12分)对于函数,若存在,使成立,则称为的不动点.已知函数.(1)当时,求函数的不动点;(2)若对任意实数,函数恒有两个相异的不动点,求的取值范围;(3)在(2)的条件下,若f(x)的两个不动点为,且,求实数的取值范围.答案1----5DCADD6--10BBDDB11---12DD13.14.或15.1:2:316.(2)(3)17.证明如图,连接MN. M,N分别是所在棱的中点,∴四边形AMB1N和四边形MNCD是平行四边形.∴MB1∥AN,CN∥MD.又 MB1⊂平面MDB1,MD⊂平面MDB1,MB1∩MD=M,∴MB1∥平面ANC,MD∥平面ANC.∴平面MDB1∥平面ANC.18.(1)对于函数, ,∴,其值域为集合.对于函数, ,∴,其值域为集合B=[1,2].∴AB={2}.……6分(2) ,∴CB.当时,即时,C=,满足条件;当时,即时,要使CB,则,解得.综上可得:.……12分19.(本小题满分12分)解:(I)过P作PE⊥CD于E,过P作PO⊥平面ABCD,垂足为O,…………………1分则PE⊥CD,E为CD的中点,O为正方形ABCD的中心. 正四棱...