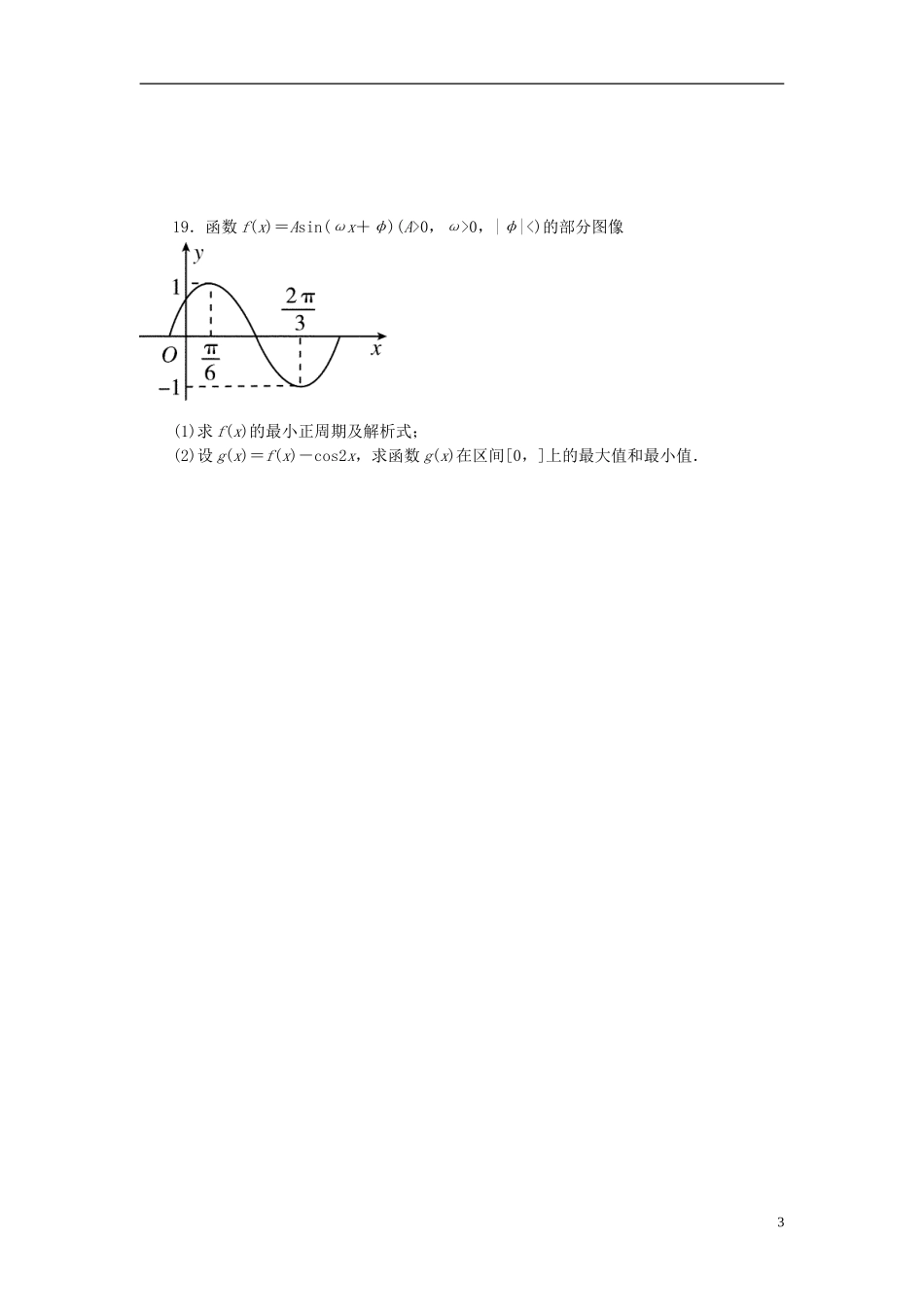
浙江省富阳市场口中学高三数学三角函数的图像和性质2复习练习1下列函数中,周期为π,且在[,]上为减函数的是()A.y=sin(2x+)B.y=cos(2x+)C.y=sin(x+)D.y=cos(x+)2.函数y=2cos2x的一个单调增区间是()A.(-,)B.(0,)C.(,)D.(,π)3.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=处取得最小值,则()A.f(x+)一定是偶函数B.f(x+)一定是奇函数C.f(x-)一定是偶函数D.f(x-)一定是奇函数4.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期为π,且当x∈[-,0)时,f(x)=sinx,则f(-)的值为()A.-B.C.-D.5.函数y=-xcosx的部分图像是()6.关于x的函数f(x)=sin(πx+φ)有以下命题:①∀φ∈R,f(x+2π)=f(x);②∃φ∈R,f(x+1)=f(x);③∀φ∈R,f(x)都不是偶函数;④∃φ∈R,使f(x)是奇函数.其中假命题的序号是()A.①③B.①④C.②④D.②③7.已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π.若f(x)的最小正周期为6π,且当x=时,f(x)取得最大值,则()A.f(x)在区间[-2π,0]上是增函数B.f(x)在区间[-3π,-π]上是增函数C.f(x)在区间[3π,5π]上是减函数D.f(x)在区间[4π,6π]上是减函数8.设函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|<)的最小正周期为π,且f(-x)=f(x),则()A.f(x)在(0,)单调递减B.f(x)在(,)单调递减C.f(x)在(0,)单调递增D.f(x)在(,)单调递增9.已知函数y=2sin(wx+θ)为偶函数(0<θ<π),其图像与直线y=2的某两个交点横坐标为x1、x2,若|x2-x1|的最小值为π,则()A.w=2,θ=B.w=-,θ=C.w=,θ=D.w=2,θ=10.已知函数y=sin在区间[0,t]上至少取得2次最大值,则正整数t的最小值是()A.6B.7C.8D.911.将函数y=sin(6x+)图像上各点的横坐标伸长到原来的3倍,再向右平移个单位,得到的函数的一个对称中心是()A.(,0)B.(,0)C.(,0)D.(,0)12.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.1已知时间t=0时,点A的坐标是(,),则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12]D.[0,1]和[7,12]13.设函数y=2sin(2x+)的图像关于点P(x0,0)成中心对称,若x0∈[-,0]则x0=______14.将函数y=sin(ωx+φ)(<φ<π)的图像,仅向右平移,或仅向左平移,所得到的函数图像均关于原点对称,则ω=________.15.已知函数f(x)=sinx+acosx的图像的一条对称轴是x=,则函数g(x)=asinx+cosx的初相是________.16.已知函数f(x)=2sin(ωx+φ)(ω>0)的图像关于直线x=对称,且f()=0,则ω的最小值为________.17.若函数y=f(x)同时具有下列三个性质:(1)最小正周期为π;(2)图像关于直线x=对称;(3)在区间[-,]上是增函数,则y=f(x)的解析式可以是______.18.已知函数f(x)=2cos2x+2sinxcosx-1(x∈R).(1)求函数f(x)的周期、对称轴方程;(2)求函数f(x)的单调增区间.219.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的部分图像(1)求f(x)的最小正周期及解析式;(2)设g(x)=f(x)-cos2x,求函数g(x)在区间[0,]上的最大值和最小值.3