广东省广州育才中学高三数学 综合训练《轨迹方程问题》VIP免费

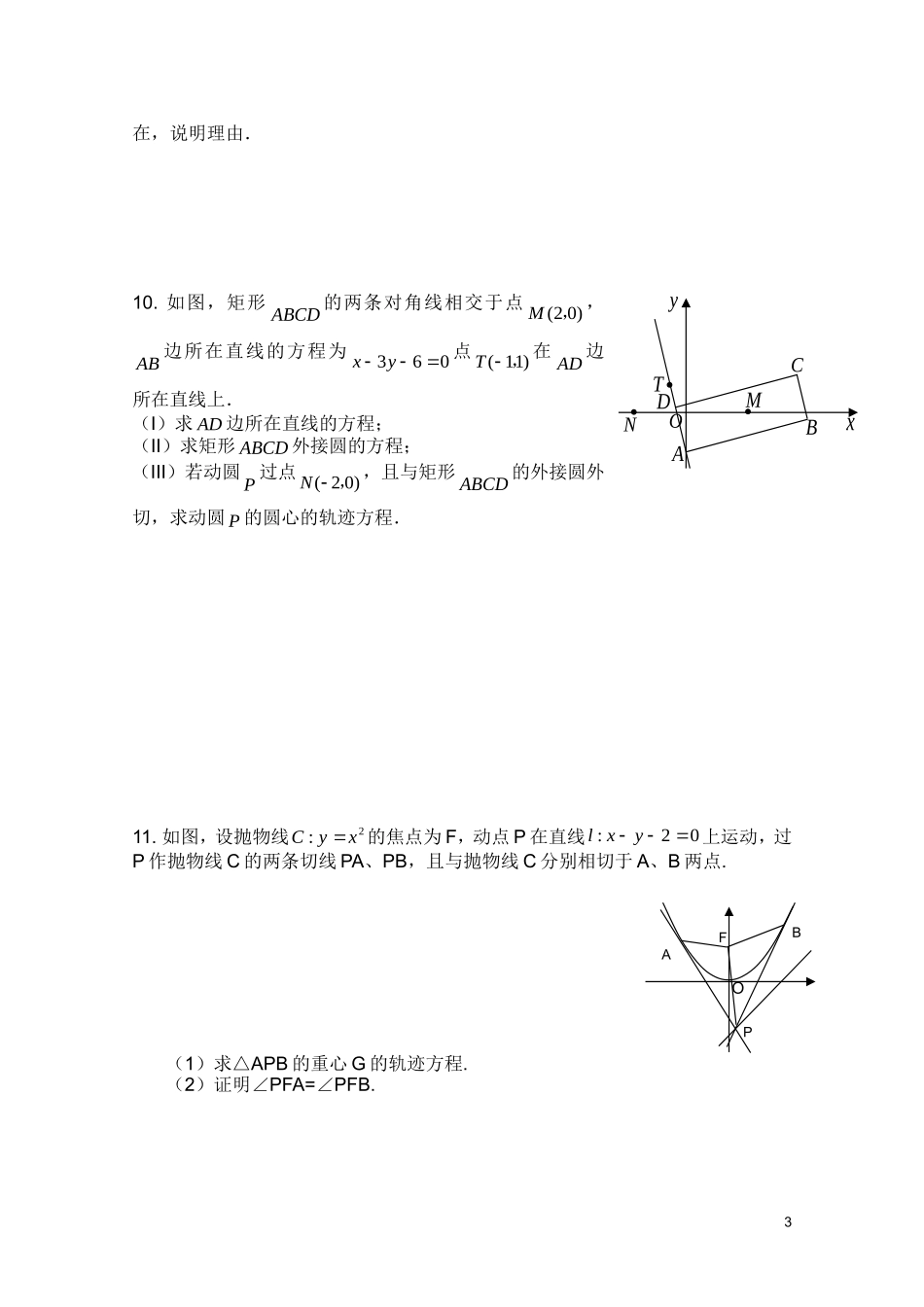
广州育才中学高三数学各类题型综合训练系列轨迹方程问题1.已知平面//平面，直线l，点lP，平面、间的距离为4，则在内到点P的距离为5且到直线l的距离为29的点的轨迹是（）A.一个圆B.两条平行直线C.四个点D.两个点2在四棱锥ABCDP中，AD面PAB，BC面PAB，底面ABCD为梯形，AD=4，BC=8，AB=6，CPBAPD，满足上述条件的四棱锥的顶点P的轨迹是（）A.圆B.不完整的圆C.抛物线D.抛物线的一部分3.如图,定点A和B都在平面内，定点P,PB,C是内异于A和B的动点。且ACPC，那么动点C在平面内的轨迹是（）A.一条线段，但要去掉两个点B.一个圆，但要去掉两个点C.一个椭圆，但要去掉两个点D.半圆，但要去掉两个点4.如图3，在正方体1111DCBAABCD中，P是侧面1BC内一动点，若P到直线BC与直线11DC的距离相等，则动点P的轨迹所在的曲线是（）A.直线B.圆C.双曲线D.抛物线图35.已知正方体1111DCBAABCD的棱长为1，点P是平面AC内的动点，若点P到1直线11DA的距离等于点P到直线CD的距离，则动点P的轨迹所在的曲线是（）A.抛物线B.双曲线C.椭圆D.直线6.已知异面直线a,b成60角，公垂线段MN的长等于2，线段AB两个端点A、B分别在a,b上移动，且线段AB长等于4，求线段AB中点的轨迹方程。7.已知圆E的方程为(x-1)2+y2=1,四边形PABQ为该圆的内接梯形，底AB为圆的直径且在x轴上，以A、B为焦点的椭圆C过P、Q两点．(1)若直线QP与椭圆C的右准线相交于点M，求点M的轨迹；(2)当梯形PABQ周长最大时，求椭圆C的方程．8.已知双曲线的两个焦点分别为F1、F2，其中F1又是抛物线y2=4x的一个焦点，且点A(-1,2)，B(3,2)在双曲线上．(1)求点F2的轨迹;(2)是否存在直线y=x+m与点F2的轨迹有且只有两个公共点，若存在，求出实数m的值，若不存在，说明理由．9.已知常数a>0，c=(0,a)，i=(1,0)，经过原点O，以c+λi为方向向量的直线与经过定点A(0,a)，以i-2λc为方向向量的直线交于点P，其中λ∈R，试问：是否存在两个定点E,F，使得|PE|+|PF|为定值，若存在，求出E,F的坐标，若不存2在，说明理由．10.如图，矩形ABCD的两条对角线相交于点(20)M，，AB边所在直线的方程为360xy点(11)T，在AD边所在直线上．（I）求AD边所在直线的方程；（II）求矩形ABCD外接圆的方程；（III）若动圆P过点(20)N，，且与矩形ABCD的外接圆外切，求动圆P的圆心的轨迹方程．11.如图，设抛物线2:xyC的焦点为F，动点P在直线02:yxl上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.（1）求△APB的重心G的轨迹方程.（2）证明∠PFA=∠PFB.3DTNOABCMxyOABPF12.已知椭圆)0(12222babyax的左、右焦点分别是F1（－c，0）、F2（c，0），Q是椭圆外的动点，满足.2||1aQF点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足.0||,022TFTFPT（Ⅰ）设x为点P的横坐标，证明xacaPF||1；（Ⅱ）求点T的轨迹C的方程；（Ⅲ）试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S=.2b若存在，求∠F1MF2的正切值；若不存在，请说明理由.13.过抛物线y2=4x的焦点的直线l与抛物线交于A、B两点，O为坐标原点.求△AOB的重心G的轨迹C的方程.14.已知圆22:1Cxy和点(2,0)Q，动点M到圆C的切线长与||MQ的比等于常数(0)，求动点M的轨迹方程，并说明它表示什么曲线？415.如图，圆1O与圆2O的半径都是1，421OO，过动点P分别作圆1O、圆2O的切线PM、PN（M、N分别为切点），使得PNPM2．试建立适当的坐标系，并求动点P的轨迹方程．16.已知椭圆C：xy221691和点P（1，2），直线l经过点P并与椭圆C交于A、B两点，求当l倾斜角变化时，弦中点的轨迹方程。17.已知棱长为3的正方体ABCDABCD1111中，长为2的线段MN的一个端点在DD1上运动，另一个端点N在底面ABCD上运动，求MN中点P的轨迹与正方体的面所围成的几何体的体积。18.（经典问题，值得一做，很能训练学生的思维能力）三峡工程需修建一个土石基坑，基坑成矩形ABCD，按规定，挖出的土方必须沿道路PA或PB送到P点处。已知mABmBCmPBmPA160,60,150,100，能否在池中确5定一条界线，使得位于界线一侧的点沿道路PA送土方较近，而另一侧的...