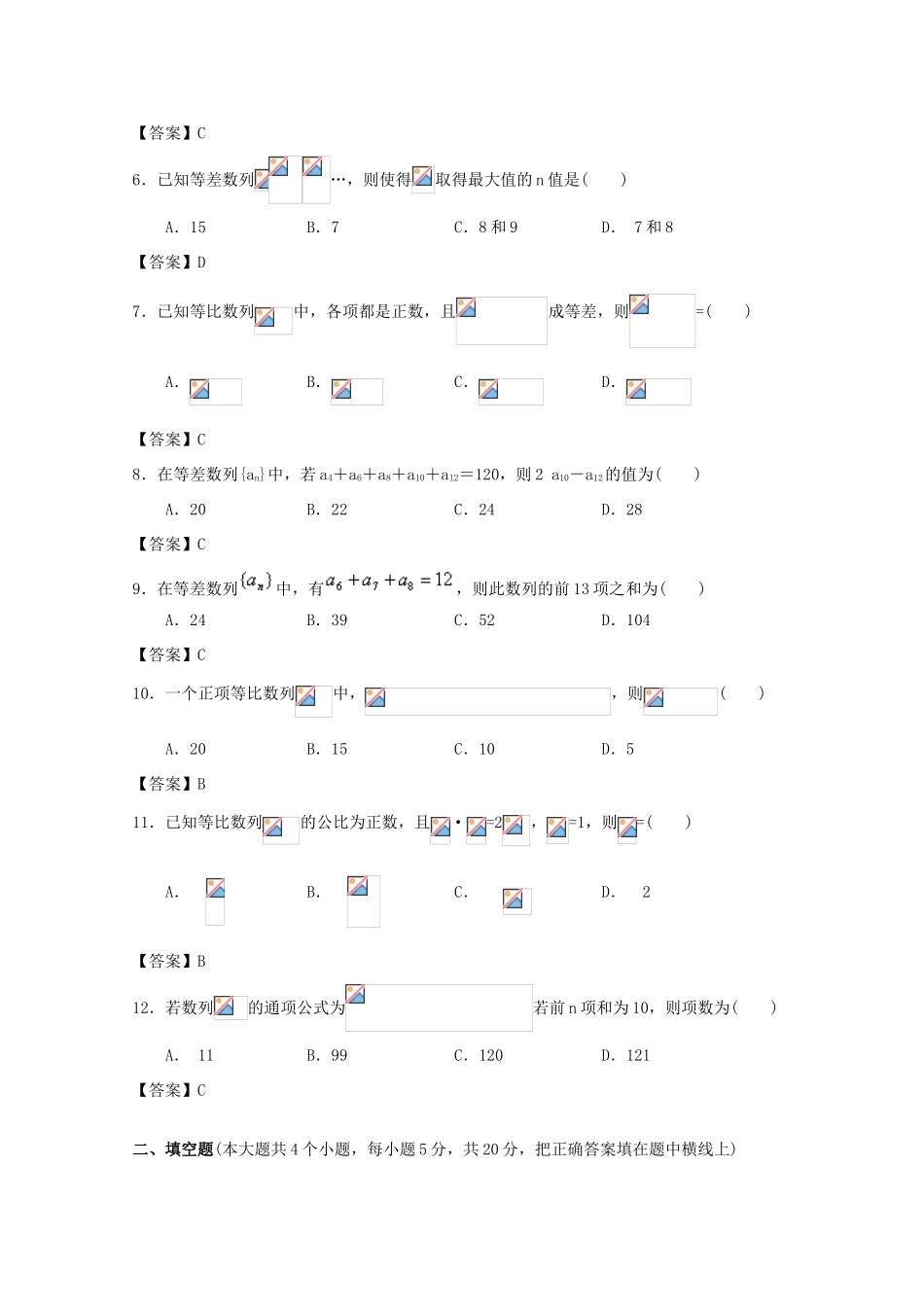
数列一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.数列的通项公式为,则数列各项中最小项是()A.第4项B.第5项C.第6项D.第7项【答案】B2.已知两个等差数列和的前n项和分别An和Bn,且,则使得为整数的正整数n的值是()A.1,3,5,8,11B.所有正整数C.1,2,3,4,5D.1,2,3,5,11【答案】D3.等差数列的前n项和为,若为一确定常数,则下列各式也为确定常数的是()A.B.C.D.【答案】C4.设等比数列{}的公比q=2,前n项和为S。,则的值为()A.B.C.D.【答案】A5.利用数学归纳法证明“”时,从“”变到“”时,左边应增乘的因式是()A.B.C.D.【答案】C6.已知等差数列…,则使得取得最大值的n值是()A.15B.7C.8和9D.7和8【答案】D7.已知等比数列中,各项都是正数,且成等差,则=()A.B.C.D.【答案】C8.在等差数列{an}中,若a4+a6+a8+a10+a12=120,则2a10-a12的值为()A.20B.22C.24D.28【答案】C9.在等差数列中,有,则此数列的前13项之和为()A.24B.39C.52D.104【答案】C10.一个正项等比数列中,,则()A.20B.15C.10D.5【答案】B11.已知等比数列的公比为正数,且·=2,=1,则=()A.B.C.D.2【答案】B12.若数列的通项公式为若前n项和为10,则项数为()A.11B.99C.120D.121【答案】C二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.已知数列(),其前项和为,给出下列四个命题:①若是等差数列,则三点、、共线;②若是等差数列,且,,则、、…、这个数中必然存在一个最大者;③若是等比数列,则、、()也是等比数列;④若(其中常数),则是等比数列.其中正确命题的序号是.(将你认为的正确命题的序号都填上)【答案】①④14.设为等差数列的前项和,若,,则当取得最大值时,的值为。【答案】4或515.各项都是正数的等比数列{}的公比q≠1,且,,成等差数列,则=____________【答案】16.已知等差数列{an}的公差不为0,且a1,a3,a9成等比数列,则=【答案】三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.数列满足:(1)求数列的通项公式;(2)设数列的前n项和分别为An、Bn,问是否存在实数,使得为等差数列?若存在,求出的值;若不存在,说明理由。【答案】(1)由∵∴∴是首项为是等比数列。故(2)∵∴又∴故当且仅当为等差数列18.已知等差数列满足,,为的前项和.(Ⅰ)若,求;(Ⅱ)求数列的前项和.【答案】(I)由已知得得解得(II)(1)(2)(2)—(1)得:∴19.已知数列{an}满足Sn+an=2n+1,(1)写出a1,a2,a3,并推测an的表达式;(2)用数学归纳法证明所得的结论。【答案】(1)a1=,a2=,a3=,猜测an=2-(2)证明:①由(1)已得当n=1时,命题成立;②假设n=k时,命题成立,即ak=2-,当n=k+1时,a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,∴2ak+1=2+2-,ak+1=2-,即当n=k+1时,命题成立.综合(1),(2)可知:对于任意正整数n,都有20.已知数列满足.(1)求数列的通项公式;(2)求满足的最小正整数m的值.【答案】(1)由,,∴数列{}是首项为3,公比为3的等比数列,∴,∴(2)由1知.令,解得故所求的最小值为5.21.已知二次函数的图象过点,且,(1)求的解析式;(2)若数列满足,且,求数列的通项公式;(3)对于(2)中的数列,求证:①;②【答案】(1)由已知得(2)累加法可求(3)①当n≥2时,,<5②∵∴22.已知等差数列满足:.(1)求的通项公式;(2)若,求数列的前n项和.【答案】(1)设的首项为,公差为,则由得解得所以的通项公式(2)由得..