高考数学一轮复习 极值最值知识梳理2 苏教版VIP免费

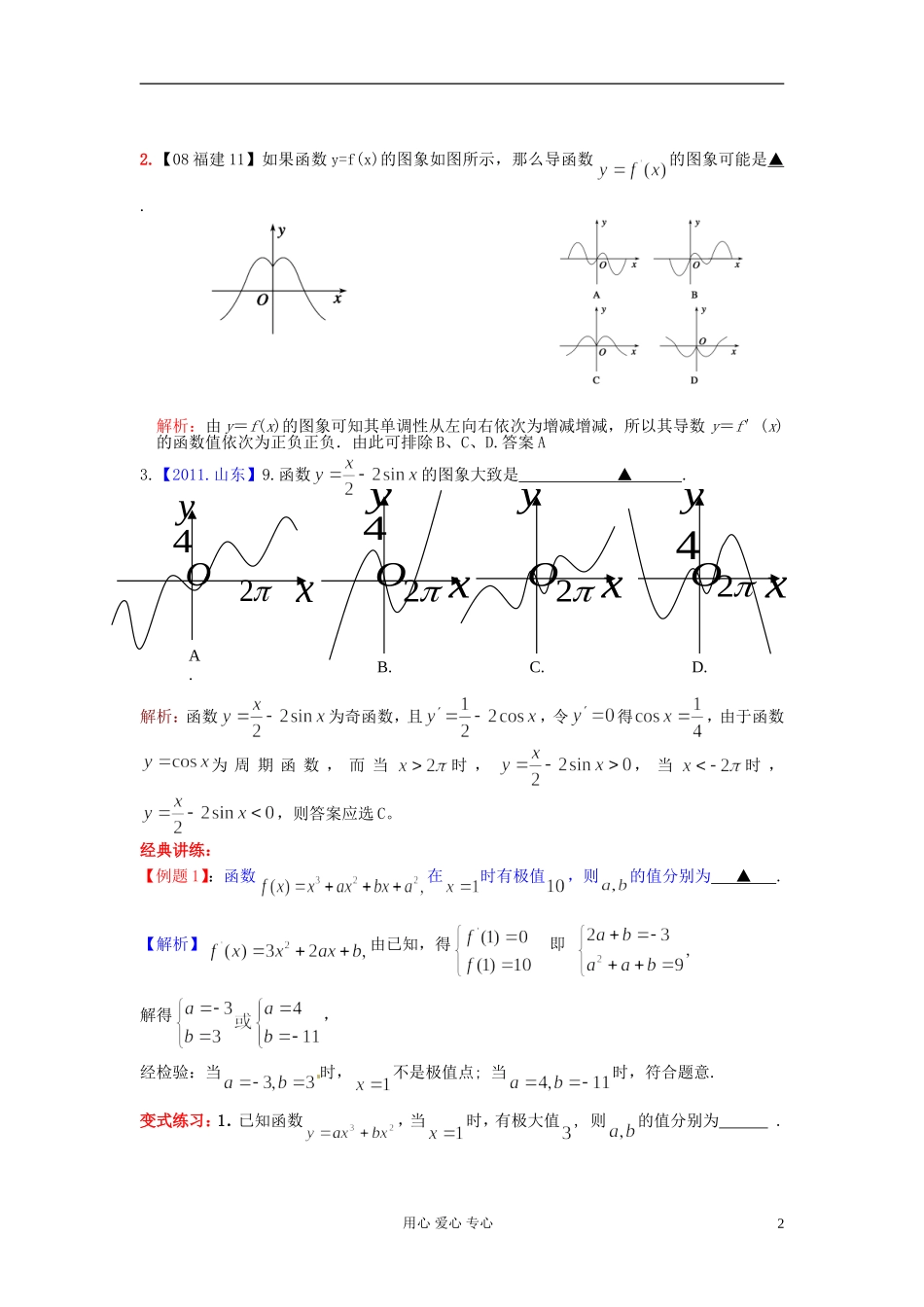
)(4xf)(1xfoaX1X2X3X4baxy函数极值与最值一、考点说明：导数法处理函数的极值与最值是36个B级考点之一36个B级要求知识点的考查比例要达到60%以上。尤其是导数的运算及运用等，仍为考查重点。08年填空题14题以三次函数为模型考查。17题以实际应用为载体考查。09年填空题3题以三次函数为模型考查。10年填空题14题以分式函数和实际应用为模型结合考查。20题以指对函数模型考查。11年填空题12题以指对函数为模型考查。19题以三次函数和二次函数为模型综合考查。应重视导数题的考查,以中档题为主。小题中两年都考了三次函数,应该更加关注指、对数函数,三角函数的导数及相关的超越函数.二、知识梳理：1.在定义中，取得极值的点称为极值点，极值点是自变量的值，极值指的是函数值。请注意以下几点：（ⅰ）极值是一个局部概念。由定义，极值只是某个点的函数值与它附近点的函数值比较是最大或最小。并不意味着它在函数的整个的定义域内最大或最小。（ⅱ）函数的极值不是唯一的。即一个函数在某区间上或定义域内极大值或极小值可以不止一个。（ⅲ）极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值，如下图所示，是极大值点，是极小值点，而>。（ⅳ）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点。而使函数取得最大值、最小值的点可能在区间的内部，也可能在区间的端点。由上图可以看出，在函数取得极值处，如果曲线有切线的话，则切线是水平的，从而有。但反过来不一定。基础体验：1.【湖南株洲08届二检】已知函数)(xfy的导函数)(xfy的图像如下，则▲.A．函数)(xf有1个极大值点，1个极小值点B．函数)(xf有2个极大值点，2个极小值点C．函数)(xf有3个极大值点，1个极小值点D．函数)(xf有1个极大值点，3个极小值点用心爱心专心1Xy1xx4OoO2x3x2.【08福建11】如果函数y=f(x)的图象如图所示，那么导函数的图象可能是▲.解析：由y＝f(x)的图象可知其单调性从左向右依次为增减增减，所以其导数y＝f′(x)的函数值依次为正负正负．由此可排除B、C、D.答案A3.【2011.山东】9.函数的图象大致是▲.解析：函数为奇函数，且，令得，由于函数为周期函数，而当时，，当时，，则答案应选C。经典讲练：【例题1】：函数在时有极值，则的值分别为▲.【解析】由已知，得即解得，经检验：当时，不是极值点;当时，符合题意.变式练习：1．已知函数，当时，有极大值,则的值分别为.用心爱心专心22xA.Oy42xB.Oy42xC.Oy2xD.Oy4【答案】【解析】当时，，即解得.经验证:即为所求.变式练习：2．【浙江杭州11届月考】已知实数dcba,,,成等比数列，且对函数xxy)2ln(，当bx时取到极大值c，则ad等于▲.【例题2】：【10·聊城模拟】函数在内有极小值，则实数的取值范围是▲.解析：令，得(，否则函数为单调增函数)．若函数在内有极小值，则，∴变式练习：1．【09·济宁联考】若函数在内有极小值，则实数b的取值范围是▲.解析 ，由题意，函数图象如右．∴即得.【例题3：】最值的确定1.函数]4,0[,)(xxexfx的最小值是▲KS5U.02.【启东中学08综合】函数在区间上最大值与最小值分别是▲.5，-153.设,函数的最大值为1,最小值为,求常数=▲KS5U.4.【潍坊四县一校】10.设aR，若函数3axyex，xR有大于零的极值点，则▲。用心爱心专心3课外拓展:【临沂一中】22．已知函数321()1(,3Rfxxaxbxxa，b为实数）有极值，且在1x处的切线与直线01yx平行.（1）求实数a的取值范围；（2）是否存在实数a，使得函数)(xf的极小值为1，若存在，求出实数a的值；若不存在，请说明理由；【解】（1）321()1,3fxxaxbx2()2,fxxaxb由题意(1)121,fab2.ba①.02)(,)(2有两个不等实根方程有极值baxxxfxf22440,0.abab②由①、②可得，220.20.aaaa或故实数a的取值范围是),0()2,(a（2）存在8.3a由（1）可知0)(,2)(2xfbaxxxf令，22122,2.xaaaxaaax),(1x1x),(21xx2x)(2x)(xf+0－0+)(xf单调增极大值单调减极小值单调增11231)(,)...