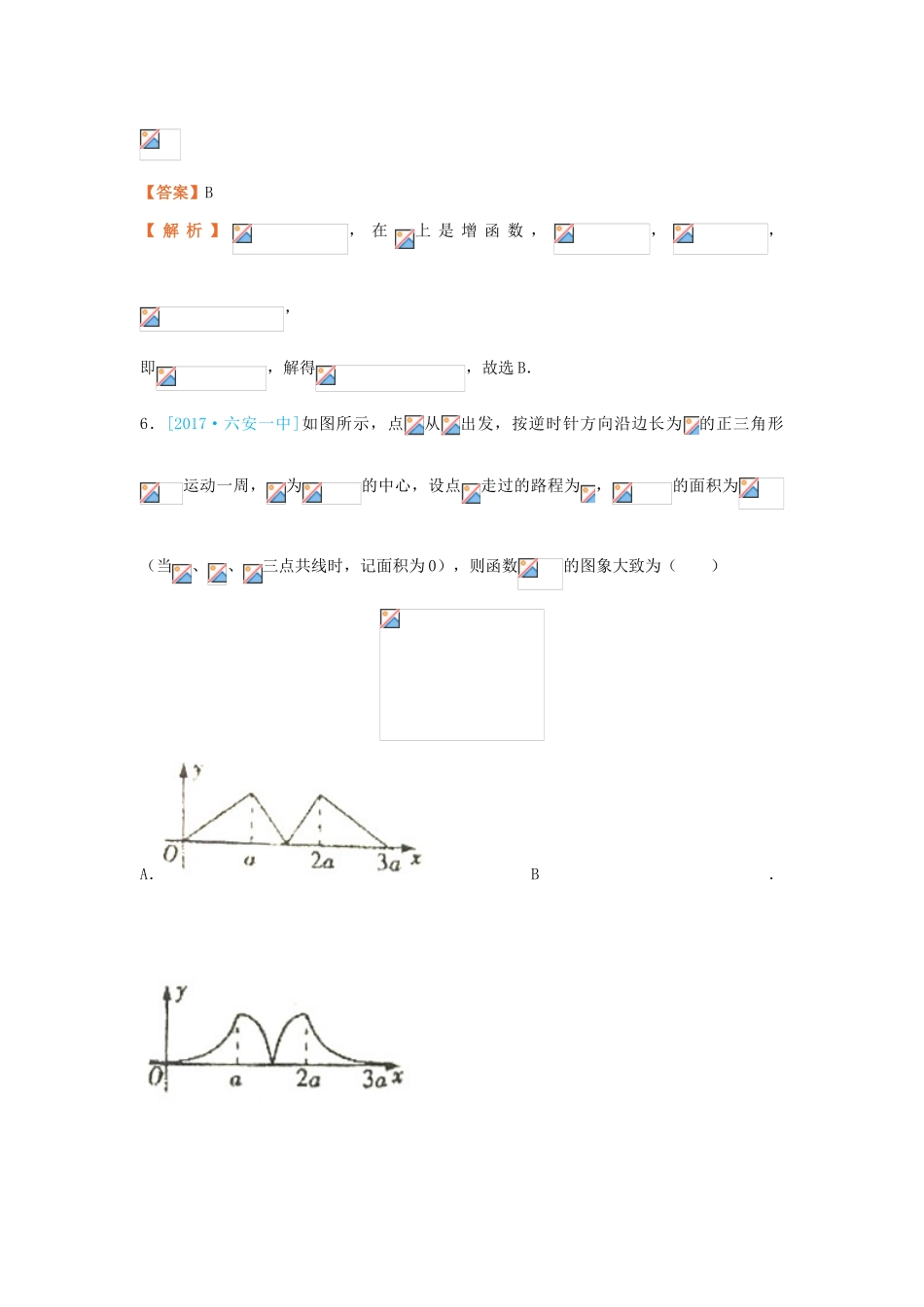
基本初等函数(2)1.[2017·沐彬中学]设,则()A.-4B.-3C.-2D.-1【答案】C【解析】由题意可得,,选C.2.[2017·德州期中]设函数的定义域为,函数的定义域为,则()A.B.C.D.【答案】C【解析】由解得,可得;由解得,可得,因此.∴,选C.3.[2017·中原名校]已知函数,若,则等于()A.B.C.D.【答案】C一、选择题(5分/题)【解析】,,,由于,因此,故答案为C.4.[2017·福清期中]如表定义函数,:则满足的的值是()A.0或1B.0或2C.1或7D.2或7【答案】D【解析】,,,,可得,可排除选项A、B;,,,,可得,排除选项C,故选D.5.[2017·新余二模]已知函数,,若存在实数,,使得,则的取值范围是()A.B.C.D.【答案】B【解析】,在上是增函数,,,,即,解得,故选B.6.[2017·六安一中]如图所示,点从出发,按逆时针方向沿边长为的正三角形运动一周,为的中心,设点走过的路程为,的面积为(当、、三点共线时,记面积为0),则函数的图象大致为()A.B.C.D.【答案】A【解析】当时,,为一次递增函数,排除选项B;当(中点)时为一次递减函数,排除选项C,D,所以选A.7.[2017·桓台二中]函数的零点所在的大致区间是()A.B.C.和D.【答案】B【解析】在上单调递增,,,所以零点所在的大致区间是,选B.8.[2017·菏泽一中]已知函数,则不等式的解集是()A.B.C.D.【答案】C【解析】∵,∴,即函数为奇函数,函数的导数,则函数是增函数,则不等式等价为,即,解得,故不等式的解集为.故选C.9.[2017·安阳模拟]已知函数(且)的图象上关于直线对称的点有且仅有一对,则实数的取值范围是()A.B.C.D.【答案】D【解析】当时,画出函数的图像如图,结合图形可以看出,此时不存在关于直线对称的点,即时不满足题设条件,故应排除答案A、B、C,应选答案D.10.[2017·安徽模拟]若函数有4个零点,则实数的取值范围是()A.B.C.D.【答案】B【解析】当时,恒成立,又,则函数在上有且只有1个零点;当时,函数,则函数在上单调递增,在上单调递减,在上单调递增,所以此时函数的极大值为,极小值为,要使得有4个零点,则,解得,故选B.11.[2017·西安联考]已知定义在R上的函数满足,在区间上是增函数,且函数为奇函数,则()A.B.C.D.【答案】A【解析】根据题意,函数满足,则有,则函数为周期为6的周期函数,若函数为奇函数,则的图象关于点成中心对称,则有,又由函数的周期为6,则有,函数为奇函数;又由函数在区间上是增函数,则函数在上为增函数,,,,则有,即.故选A.12.[2017·德化一中]已知定义在上的偶函数满足,且当时,,则函数的零点个数是()A.2B.4C.6D.8【答案】C【解析】由题意,所以周期为2,当时,,且为偶函数,即函数图象关于y轴对称,分别画出和的图象,观察可得交点个数为6个,即函数的零点个数是6个,故选C.13.[2017·会宁县一中]已知函数,满足对任意,都有成立,则的取值范围是__________.【答案】二、填空题(5分/题)【解析】因为函数对任意,都有成立,即函数为减函数,故需满足,解得,故答案为.14.[2017·朝阳期中]已知函数同时满足以下条件:①定义域为;②值域为;③.试写出一个函数解析式___________.【答案】或或(答案不唯一)【解析】函数定义域为R,值域为且为偶函数,满足题意的函数解析式可以为或或.15.[2017·盐城中学]设是定义在R上的奇函数,且满足,则________.【答案】0【解析】∵是定义在R上的奇函数,且满足,∴由奇函数性质得:,下面我们用归纳法证明对一切正整数成立.;如果,,则;所以.故答案为0.16.[2017·崇义中学]函数在区间上可找到个不同的数,,···,使得,则的最大值等于_________.【答案】10【解析】设,则条件等价为的根的个数,作出函数和的图象,由图象可知与函数在区间上最多有个交点,即的最大值为,故答案为.