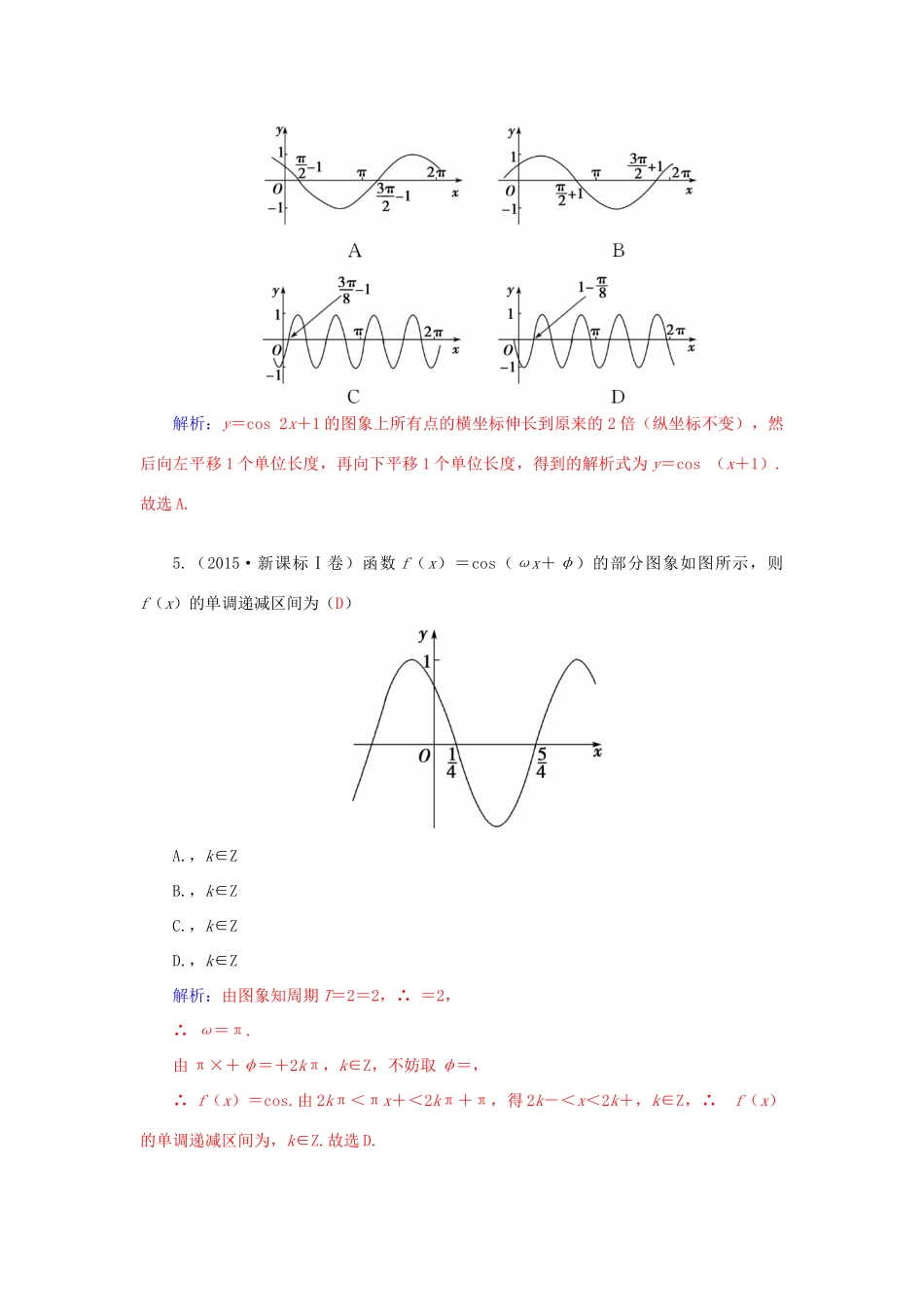
第一讲三角函数的图象与性质配套作业一、选择题1.若sin(α-π)=,α为第四象限角,则tanα=(A)A.-B.-C.D.解析:∵sin(α-π)=,∴-sinα=,sinα=-.又∵α为第四象限角,∴cosα===,tanα===-.2.定义在R上的周期函数f(x),周期T=2,直线x=2是它的图象的一条对称轴,且f(x)在[-3,-2]上是减函数,如果A,B是锐角三角形的两个内角,则(A)A.f(sinA)>f(cosB)B.f(cosB)>f(sinA)C.f(sinA)>f(sinB)D.f(cosB)>f(cosA)解析:由题意知:周期函数f(x)在[-1,0]上是减函数,在[0,1]上是增函数.又因为A,B是锐角三角形的两个内角,A+B>,得:sinA>cosB,故f(sinA)>f(cosB).综上知选A.3.函数y=2sin(0≤x≤9)的最大值与最小值之和为(A)A.2-B.0C.-1D.-1-解析:用五点作图法画出函数y=2sin(0≤x≤9)的图象,注意0≤x≤9知,函数的最大值为2,最小值为-.故选A.4.把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是(A)解析:y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的解析式为y=cos(x+1).故选A.5.(2015·新课标Ⅰ卷)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为(D)A.,k∈ZB.,k∈ZC.,k∈ZD.,k∈Z解析:由图象知周期T=2=2,∴=2,∴ω=π.由π×+φ=+2kπ,k∈Z,不妨取φ=,∴f(x)=cos.由2kπ<πx+<2kπ+π,得2k-<x<2k+,k∈Z,∴f(x)的单调递减区间为,k∈Z.故选D.6.已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<)的图象(部分)如图所示,则f(x)的解析式是(A)A.f(x)=2sin(x∈R)B.f(x)=2sin(x∈R)C.f(x)=2sin(x∈R)D.f(x)=2sin(x∈R)解析:由图象可知其周期为:4=2,∵=2,得ω=π,故只可能在A,C中选一个,又因为x=时达到最大值,用待定系数法知φ=.二、填空题7.若sinθ=-,tanθ>0,则cosθ=W.答案:-8.已知角α的终边经过点(-4,3),则cosα=W.解析:由题意可知x=-4,y=3,r=5,所以cosα==-.答案:-三、解答题9.已知函数f(x)=2cosx(sinx+cosx).(1)求f的值;(2)求函数f(x)的最小正周期及单调递增区间.分析:思路一直接将代入函数式,应用三角函数诱导公式计算.(2)应用和差倍半的三角函数公式,将函数化简sin+1.得到T==π.由2kπ-≤2x+≤2kπ+,k∈Z,解得kπ-≤x≤kπ+,k∈Z.思路二先应用和差倍半的三角函数公式化简函数f(x)=2sinxcosx+2cos2x=sin+1.(1)将代入函数式计算;(2)T==π.由2kπ-≤2x+≤2kπ+,k∈Z,解得kπ-≤x≤kπ+,k∈Z.解析:解法一(1)f=2cos=-2cos=2.(2)因为f(x)=2sinxcosx+2cos2x=sin2x+cos2x+1=sin+1.所以T==π.由2kπ-≤2x+≤2kπ+,k∈Z,得kπ-≤x≤kπ+,k∈Z,所以f(x)的单调递增区间为,k∈Z.解法二因为f(x)=2sinxcosx+2cos2x=sin2x+cos2x+1=sin+1.(1)f=sin+1=sin+1=2.(2)T==π.由2kπ-≤2x+≤2kπ+,k∈Z,得kπ-≤x≤kπ+,k∈Z,所以f(x)的单调递增区间为,k∈Z.10.函数f(x)=Asin+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为.(1)求函数f(x)的解析式;(2)设α∈,则f=2,求α的值.解析:(1)∵函数f(x)的最大值为3,∴A+1=3,即A=2.∵函数图象的相邻两条对称轴之间的距离为,∴最小正周期为T=π,∴ω=2,故函数f(x)的解析式为y=2sin+1.(2)∵f=2sin+1=2,即sin=,∵0<α<,∴-<α-<.∴α-=,故α=.11.(2015·北京卷)已知函数f(x)=sincos-sin2.(1)求f(x)的最小正周期;(2)求f(x)在区间[-π,0]上的最小值.解析:(1)由题意得f(x)=sinx-(1-cosx)=sin-,所以f(x)的最小正周期为2π.(2)因为-π≤x≤0,所以-≤x+≤.当x+=-,即x=-时,f(x)取得最小值.所以f(x)在区间[-π,0]上的最小值为f=-1-.