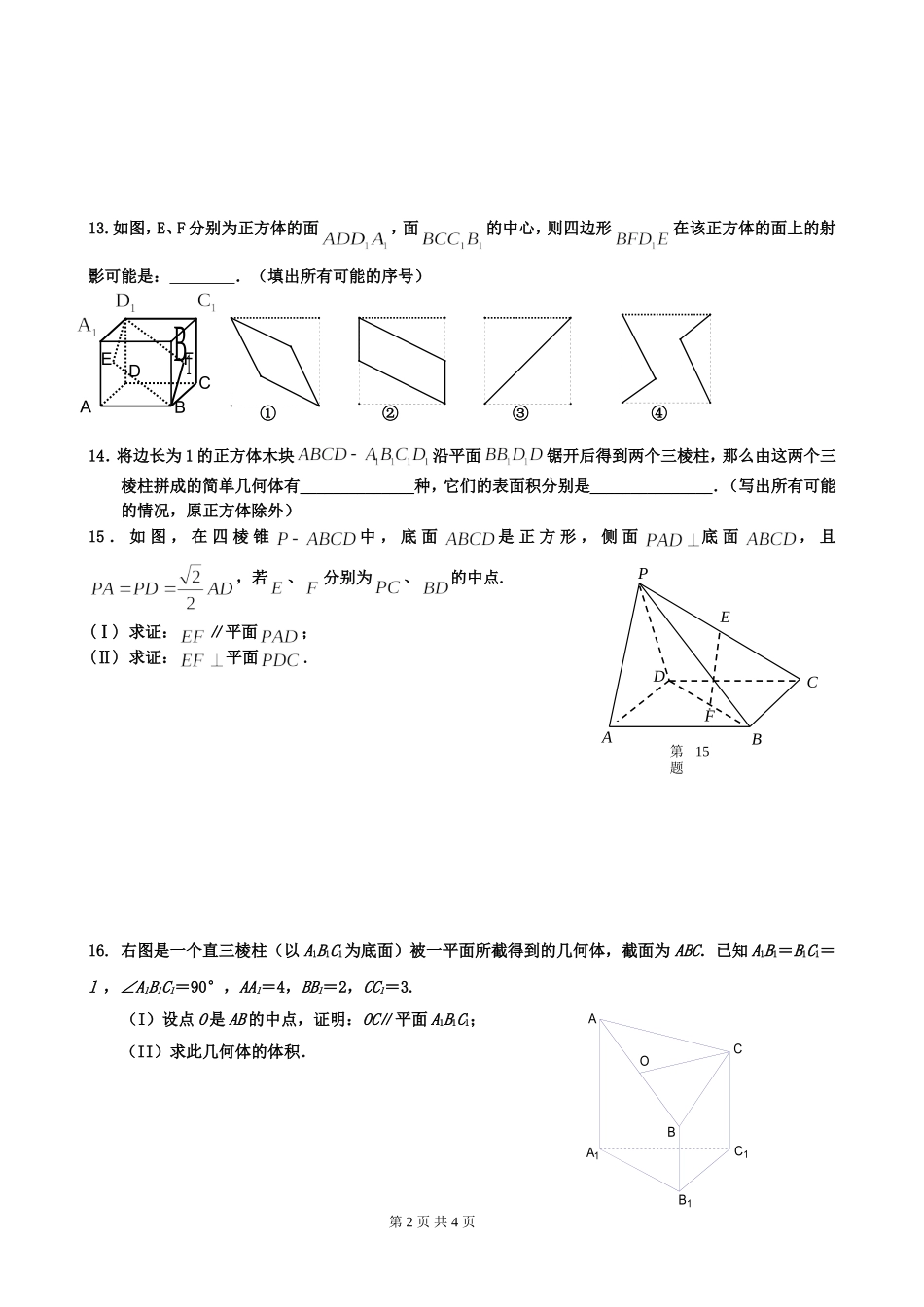
震川中学高二数学综合练习一1.已知为不垂直的异面直线,是一个平面,则在上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.在上述结论中,正确结论的序号有(写出所有正确结论的序号).2.已知平面α内有无数条直线都与平面β平行,那么α与β的关系是.3.平面α∥平面β,AB、CD是夹在α和β间的两条线段,E、F分别为AB、CD的中点,则EF与α的关系是.4.若正方体的所有顶点都在球面上,则正方体的体积与球的体积之比为.5.一个正三棱柱的三视图如图所示,则这个正三棱柱的侧面积为.6.设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若,则;其中正确命题的序号是.7.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为.8.已知一圆锥的母线长是5cm,高为4cm,则该圆锥的表面积是.9.空间四边形中,、分别是、的中点,=3、=4、=,那么与所成角的度数是______度10.右图是正方体平面展开图,在这个正方体中①BM与ED平行;②CN与BE是异面直线;③CN与BM成角;④EM与BN垂直。以上命题中正确命题的序号是11.已知正四棱锥的底面边长为2,侧棱长为,则侧面与底面所成的二面角为12.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆上的一点,则图中互相垂直的平面共有_____________对。第1页共4页MEDCABNFAPCBD1OA1B1C1BACD32FABCPDE第15题13.如图,E、F分别为正方体的面,面的中心,则四边形在该正方体的面上的射影可能是:.(填出所有可能的序号)①②③④14.将边长为1的正方体木块沿平面锯开后得到两个三棱柱,那么由这两个三棱柱拼成的简单几何体有______________种,它们的表面积分别是_______________.(写出所有可能的情况,原正方体除外)15.如图,在四棱锥中,底面是正方形,侧面底面,且,若、分别为、的中点.(Ⅰ)求证:∥平面;(Ⅱ)求证:平面.16.右图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3.(I)设点O是AB的中点,证明:OC∥平面A1B1C1;(II)求此几何体的体积.第2页共4页BCDEF1BAABOCB1C1A117.如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥AD,BE∥AF,G、H分别是FA、FD的中点。(Ⅰ)证明:四边形BCHG是平行四边形;(Ⅱ)求证:平面BCE∥平面ADF;(Ⅲ)C、D、E、F四点是否共面?为什么?(Ⅳ)设AB=BE,证明:平面ADE⊥平面BCHG.18.四棱锥中,平面,四边形是矩形,、分别是、的中点.若,.(Ⅰ)求证:平面;(Ⅱ)求点到平面的距离;(Ⅲ)求直线平面所成角的正弦值.第3页共4页GHFEDCBA20.如图,在组合体中,是一个长方体,是一个四棱锥.,,点且.(Ⅰ)证明:;(Ⅱ)求与平面所成的角的正切值;(Ⅲ)若,当为何值时,.第4页共4页D1A1C1B1ABDCOPD1C1B1A1PDCBA震川中学高二数学综合练习一参考答案:(1)①②④;(2)平行或相交;(3)平行;(4);(5);(6)①②③;(7);(8);(9);(10)③④;(11);(12)3对;(13)②③;(14)3种;,(15)证明:(Ⅰ)连结AC,则是的中点,在△中,EF∥PA且PA平面PAD,EF平面PAD,∴EF∥平面PAD(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA又PA=PD=AD,所以△PAD是等腰直角三角形,且,即PA⊥PD而CD∩PD=D,∴PA⊥平面PDC,又EF∥PA,所以EF⊥平面PDC(16)1)证明:作交于,连.则.……2分是的中点,.则是平行四边形,.……4分平面且平面,面.……6分(2)如图,过作截面面,分别交,于,.作于.……2分面,,则平面.又,,,.第5页共4页ABHODCC2B1C1A2A1所求几何体体积为:(17)(Ⅰ)由题意知,所以又,故所以四边形是平行四边形。(Ⅱ)略(Ⅲ)四点共面。理由如下:由,是的中点知,,所以由(Ⅰ)知,所以,故共面。又点在直线上所以四点共面。(Ⅳ)(18)(I)取PC的中点G,连结EG,FG,又由F为PD中点,则FG.…2分又由已知有∴四边形AEGF是平行四边形.…4分平面PCE,EG(II)………...