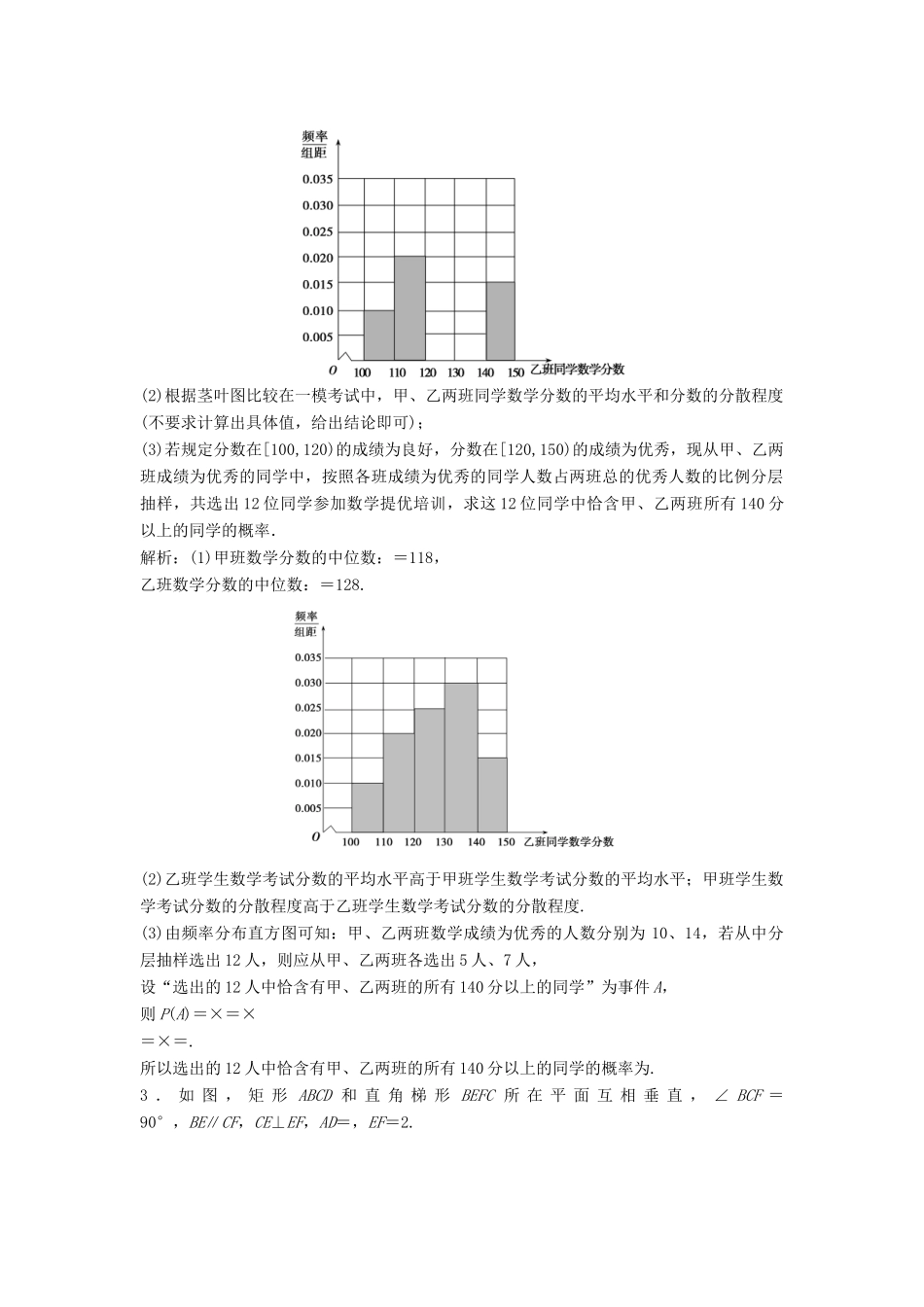
中档题保分练(四)1.(2018·唐山模拟)已知a=(2sinωx,sinωx+cosωx),b=(cosωx,(sinωx-cosωx)),0<ω<1,函数f(x)=a·b,直线x=是函数f(x)图象的一条对称轴.(1)求函数f(x)的解析式及单调递增区间;(2)在△ABC中,已知f(A)=0,c=3,a=,求b.解析:(1)f(x)=a·b=sin2ωx-cos2ωx=2sin. x=是函数f(x)图象的一条对称轴,∴f=±2,∴2×ω-=kπ+,k∈Z.∴ω=+,k∈Z. ω∈(0,1),∴k=0,ω=,∴f(x)=2sin.令2kπ-≤x-≤2kπ+,k∈Z,得2kπ-≤x≤2kπ+,k∈Z.∴f(x)=2sin,f(x)的增区间为,k∈Z.(2) f(A)=2sin=0,∴A-=kπ,∴A=kπ+,k∈Z. A∈(0,π),∴A=.在△ABC中,由余弦定理:cosA=,∴b2+c2-a2-2bccosA=0,∴b2+32-13-2b×3×=0,∴b2-3b-4=0,∴(b-4)(b+1)=0. b>0,∴b=4.2.(2018·哈师大附中模拟)哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两班本次考试数学分数如下列茎叶图所示:(1)根据茎叶图求甲、乙两班同学数学分数的中位数,并将乙班同学的分数的频率分布直方图填充完整;(2)根据茎叶图比较在一模考试中,甲、乙两班同学数学分数的平均水平和分数的分散程度(不要求计算出具体值,给出结论即可);(3)若规定分数在[100,120)的成绩为良好,分数在[120,150)的成绩为优秀,现从甲、乙两班成绩为优秀的同学中,按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样,共选出12位同学参加数学提优培训,求这12位同学中恰含甲、乙两班所有140分以上的同学的概率.解析:(1)甲班数学分数的中位数:=118,乙班数学分数的中位数:=128.(2)乙班学生数学考试分数的平均水平高于甲班学生数学考试分数的平均水平;甲班学生数学考试分数的分散程度高于乙班学生数学考试分数的分散程度.(3)由频率分布直方图可知:甲、乙两班数学成绩为优秀的人数分别为10、14,若从中分层抽样选出12人,则应从甲、乙两班各选出5人、7人,设“选出的12人中恰含有甲、乙两班的所有140分以上的同学”为事件A,则P(A)=×=×=×=.所以选出的12人中恰含有甲、乙两班的所有140分以上的同学的概率为.3.如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=,EF=2.(1)求异面直线AD与EF所成的角;(2)当AB的长为何值时,二面角AEFC的大小为45°?解析:如图,以点C为坐标原点,分别以CB,CF和CD作为x轴,y轴和z轴建立空间直角坐标系Cxyz.设AB=a,BE=b,CF=c(b