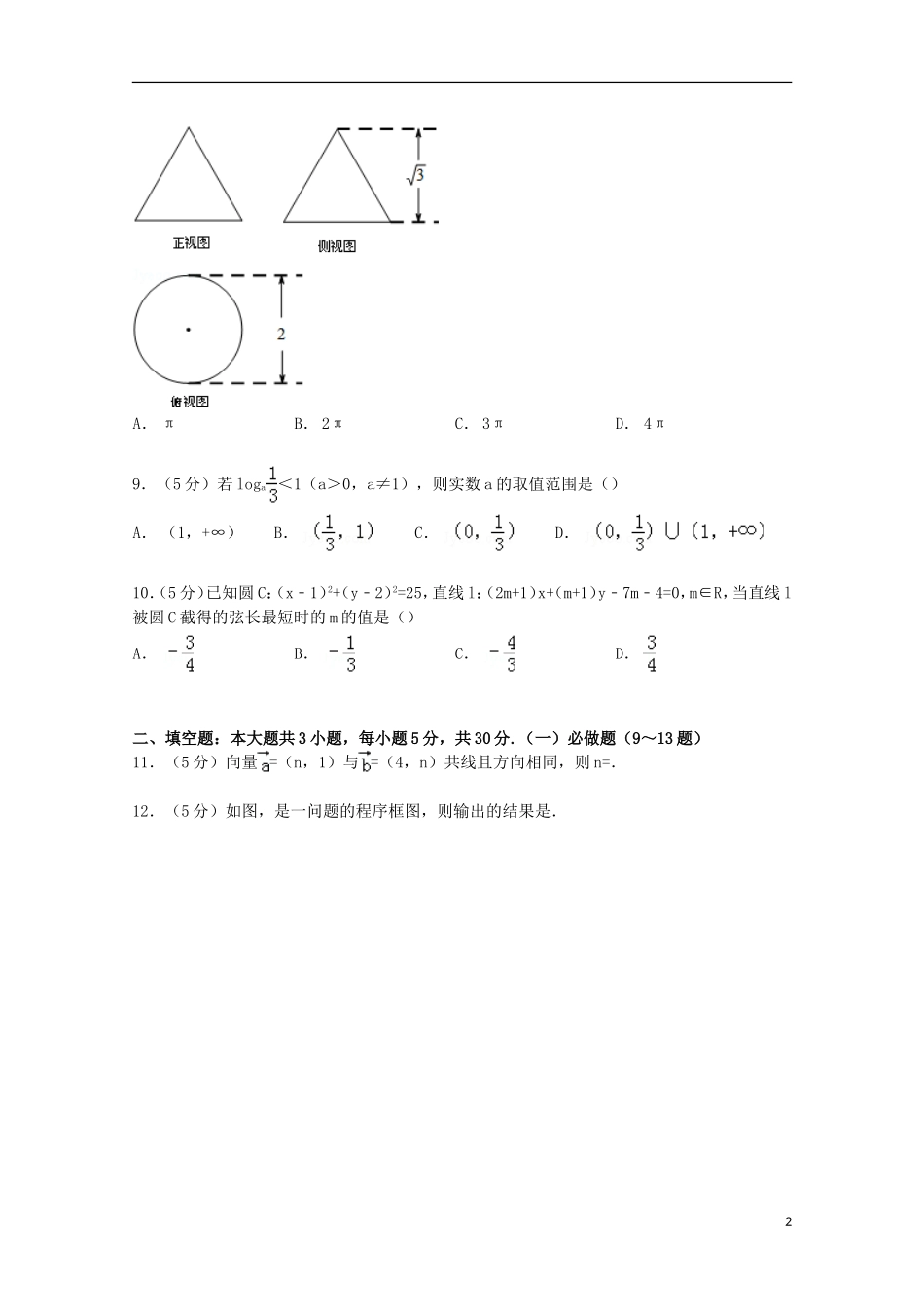
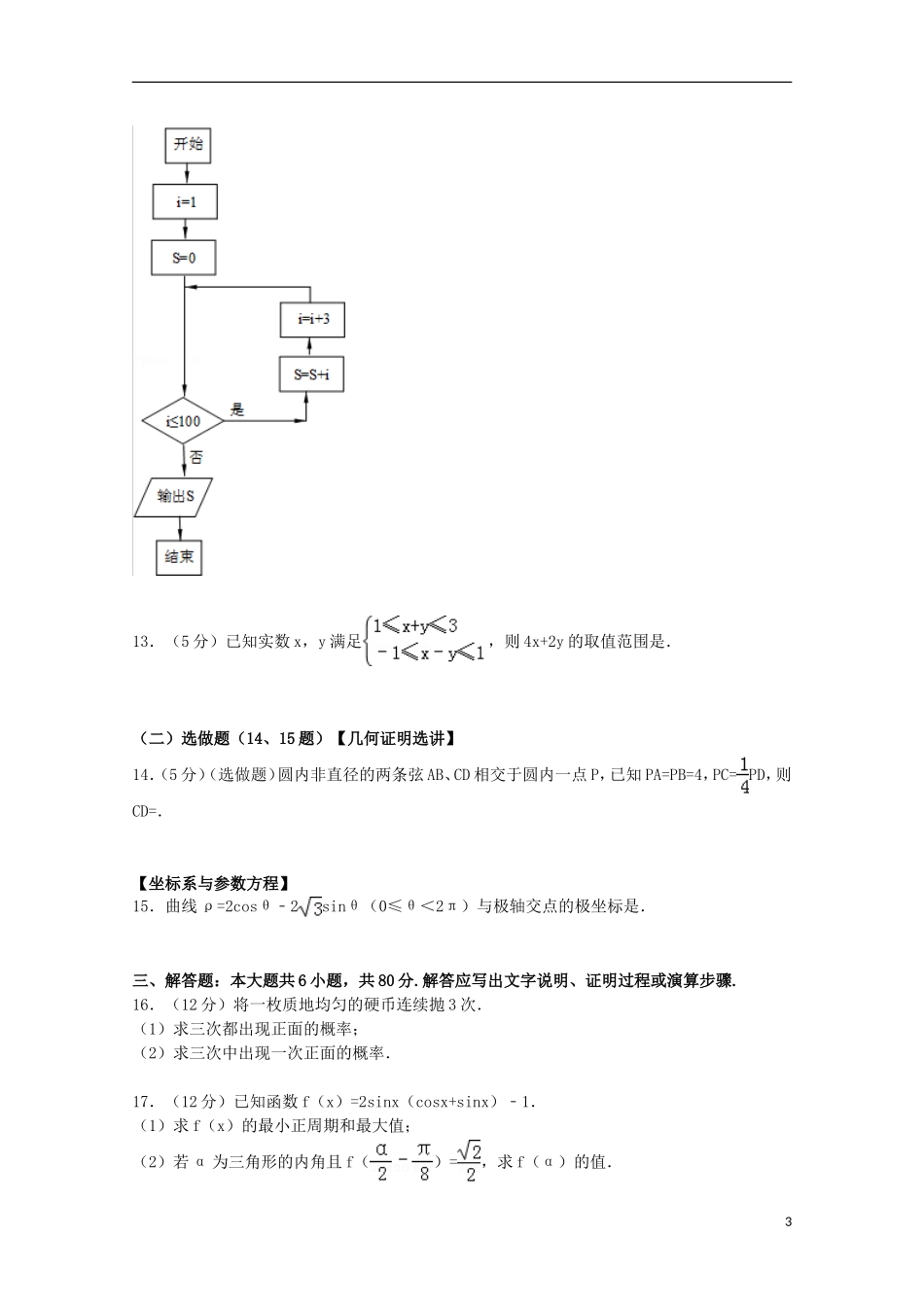
广东省广州市增城市2015届高三上学期期中数学试卷(文科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)=(i是虚数单位)()A.iB.﹣iC.2iD.﹣2i2.(5分)已知集合A={x|2≤x<4},B={x|3x﹣7≥8﹣2x},则A∩B=()A.[3,4)B.(3,4)C.[2,3]D.[2,4)3.(5分)下列等式中错误的是()A.sin(π+α)=﹣sinαB.cos(π﹣α)=cosαC.cos(2π﹣α)=cosαD.sin(2π+α)=sinα4.(5分)函数f(x)=的定义域是()A.B.C.D.5.(5分)化简=()A.B.﹣C.2yD.﹣2y﹣16.(5分)如果函数f(x)=+a是奇函数,则a的值是()A.1B.2C.﹣1D.﹣27.(5分)若直线a不平行于平面α,则下列结论成立的是()A.平面α内所有的直线都与a异面B.平面α内不存在与a平行的直线C.平面a内所有的直线都与α相交D.直线α与平面α有公共点8.(5分)如图是一个圆锥的三视图,则其侧面积是()1A.πB.2πC.3πD.4π9.(5分)若loga<1(a>0,a≠1),则实数a的取值范围是()A.(1,+∞)B.C.D.10.(5分)已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0,m∈R,当直线l被圆C截得的弦长最短时的m的值是()A.B.C.D.二、填空题:本大题共3小题,每小题5分,共30分.(一)必做题(9~13题)11.(5分)向量=(n,1)与=(4,n)共线且方向相同,则n=.12.(5分)如图,是一问题的程序框图,则输出的结果是.213.(5分)已知实数x,y满足,则4x+2y的取值范围是.(二)选做题(14、15题)【几何证明选讲】14.(5分)(选做题)圆内非直径的两条弦AB、CD相交于圆内一点P,已知PA=PB=4,PC=PD,则CD=.【坐标系与参数方程】15.曲线ρ=2cosθ﹣2sinθ(0≤θ<2π)与极轴交点的极坐标是.三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.16.(12分)将一枚质地均匀的硬币连续抛3次.(1)求三次都出现正面的概率;(2)求三次中出现一次正面的概率.17.(12分)已知函数f(x)=2sinx(cosx+sinx)﹣1.(1)求f(x)的最小正周期和最大值;(2)若α为三角形的内角且f()=,求f(α)的值.318.(14分)如图,在三棱锥V﹣ABC中,VO⊥平面ABC,O∈CD,VA=VB=,AD=BD=3,BC=5.(1)求证:VC⊥AB;(2)当二面角∠VDC=60°时,求三棱锥V﹣ABC的体积.19.(14分)设f(x)=﹣bx,b∈R(1)当b=1时,求f(x)的单调区间;(2)当f(x)在R上有且仅有一个零点时,求b的取值范围.20.(14分)已知椭圆的中心在坐标原点,一个焦点坐标是F1(0,﹣1),离心率为.(1)求椭圆的标准方程;(2)过点F1作直线交椭圆于A,B两点,F2是椭圆的另一个焦点,若=时,求直线AB的方程.21.(14分)在数列{an}中,已知a1=2,对任意正整数n都有nan+1=2(n+1)an.(1)求数列{an}的通项公式;(2)求数列{an}的前n项的和Sn;(3)如果对于一切非零自然数n都有nan≥λ(Sn﹣2)恒成立,求实数λ的最大值.广东省广州市增城市2015届高三上学期期中数学试卷(文科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)=(i是虚数单位)()A.iB.﹣iC.2iD.﹣2i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.4分析:直接利用复数代数形式的除法运算化简求值.解答:解:===i.故选:A.点评:本题考查了复数代数形式的乘除运算,复数的除法,采用分子分母同时乘以分母的共轭复数,是基础的计算题.2.(5分)已知集合A={x|2≤x<4},B={x|3x﹣7≥8﹣2x},则A∩B=()A.[3,4)B.(3,4)C.[2,3]D.[2,4)考点:交集及其运算.专题:集合.分析:先求解集合B,再按照交集的定义求解计算.解答:解:A={x|2≤x<4},B={x|3x﹣7≥8﹣2x}={x|x≥3},∴A∩B=[3,4).故选A.点评:本题考查集合的基本运算,属于基础题.3.(5分)下列等式中错误的是()A.sin(π+α)=﹣sinαB.cos(π﹣α)=cosαC.cos(2π﹣α)=cosαD.sin(2π+α)=sinα考点:运用诱导公式化简求值.专题:三角函数的图像与性质.分析:直接利用诱导公式判断选项即可.解答:解:sin(π+α)=﹣...