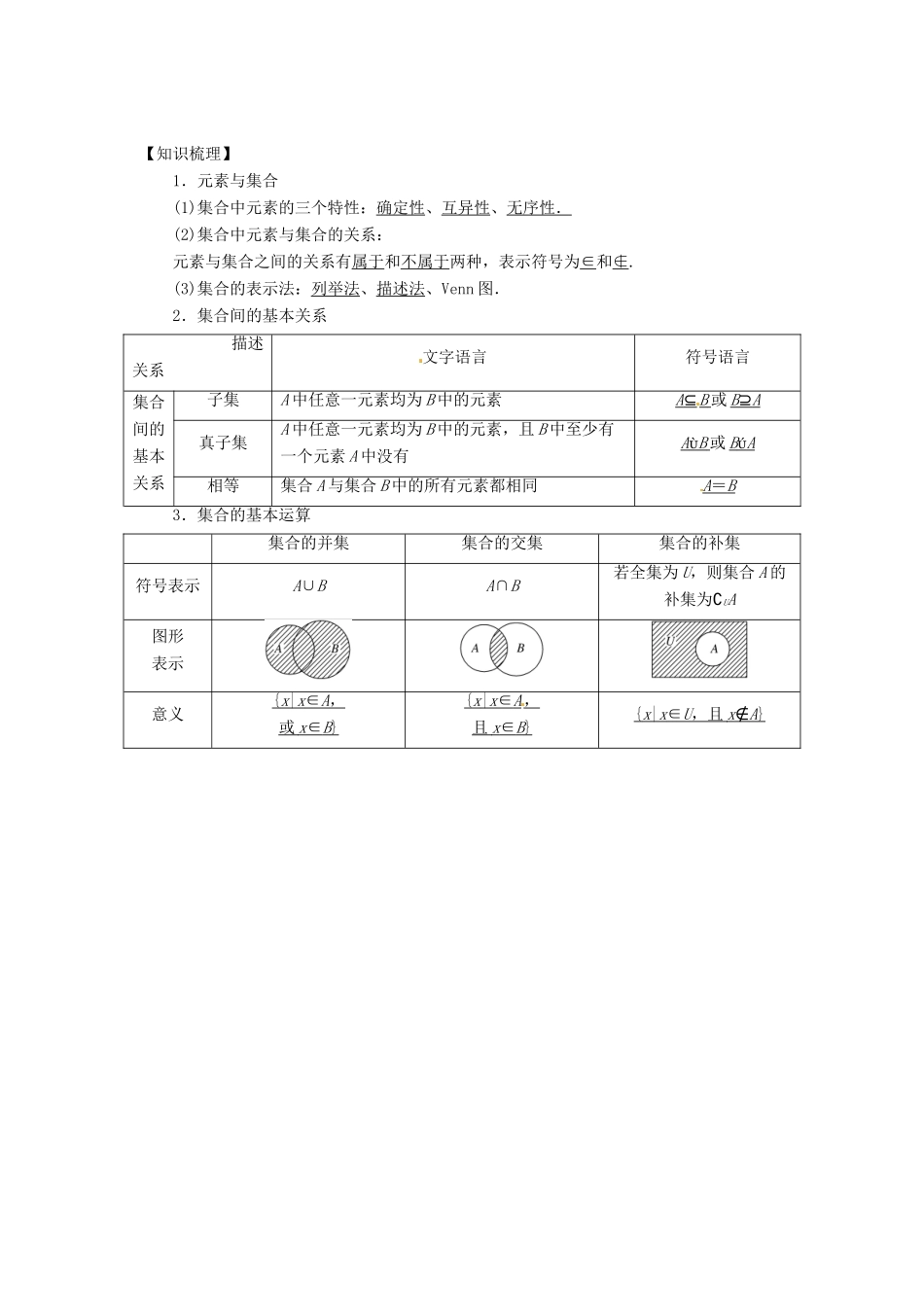
集合及其运算主标题:集合及其运算副标题:为学生详细的分析集合及其运算的高考考点、命题方向以及规律总结。关键词:集合,交集,并集,补集难度:2重要程度:4考点剖析:1.了解集合的含义、元素与集合的属于关系.2.理解集合之间包含与相等的含义,能识别给定集合的子集.3.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.4.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.5.能使用韦恩(Venn)图表达集合的关系及运算.命题方向:本部分在高考中常以选择题和填空题的形式出现,考查主要有:集合中元素的性质(确定性、互异性、无序性);元素与集合、集合与集合的关系.规律总结:1.一点提醒求集合的基本运算时,要认清集合元素的属性(是点集、数集或其他情形)和化简集合,这是正确求解集合运算的两个先决条件.如第(3)题就是混淆了数集与点集.2.两个防范一是忽视元素的互异性,如(1);二是运算不准确,尤其是运用数轴图示法时要特别注意端点是实心还是空心,如(6).3.集合的运算性质:①A∪B=B⇔A⊆B;②A∩B=A⇔A⊆B;③A∪(∁UA)=U;④A∩(∁UA)=∅.1.判断集合关系的方法有三种(1)一一列举观察;(2)集合元素特征法:首先确定集合的元素是什么,弄清集合元素的特征,再利用集合元素的特征判断集合关系;(3)数形结合法:利用数轴或Venn图.2.解决集合的综合运算的方法解决集合的综合运算时,一般先运算括号内的部分.当集合是用列举法表示的数集时,可以通过列举集合的元素进行运算;当集合是用不等式形式表示时,可运用数轴求解.3.数形结合思想数轴和Venn图是进行交、并、补集运算的有力工具,数形结合是解集合问题的常用方法,解题时要先把集合中各种形式的元素化简,使之明确化,尽可能地借助数轴、直角坐标系或Venn图等工具,将抽象的代数问题具体化、形象化、直观化,然后利用数形结合的思想方法解题.【知识梳理】1.元素与集合(1)集合中元素的三个特性:确定性、互异性、无序性.(2)集合中元素与集合的关系:元素与集合之间的关系有属于和不属于两种,表示符号为∈和∉.(3)集合的表示法:列举法、描述法、Venn图.2.集合间的基本关系描述关系文字语言符号语言集合间的基本关系子集A中任意一元素均为B中的元素A⊆B或B⊇A真子集A中任意一元素均为B中的元素,且B中至少有一个元素A中没有AB或BA相等集合A与集合B中的所有元素都相同A=B3.集合的基本运算集合的并集集合的交集集合的补集符号表示A∪BA∩B若全集为U,则集合A的补集为∁UA图形表示意义{x|x∈A,或x∈B}{x|x∈A,且x∈B}{x|x∈U,且x∉A}