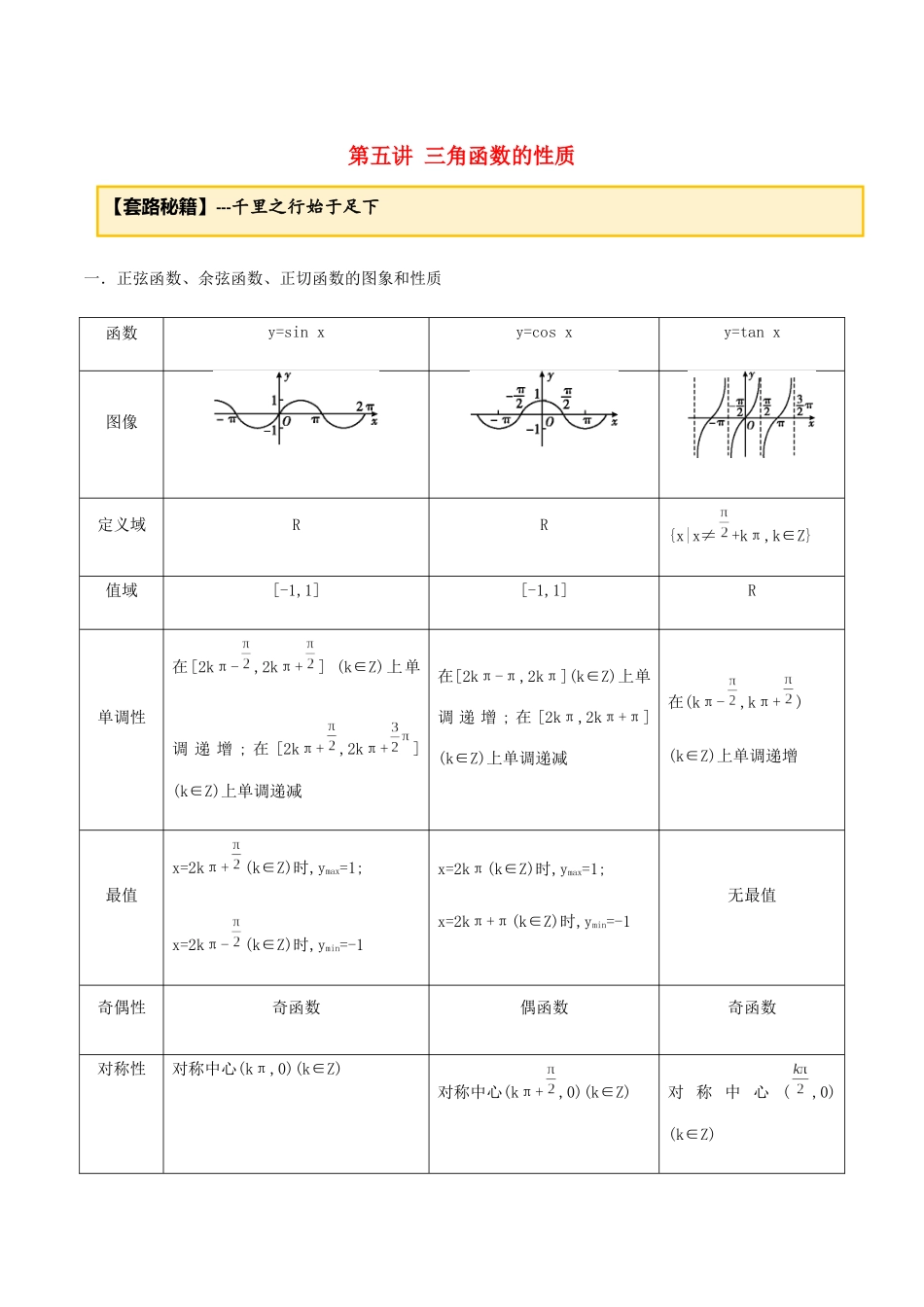
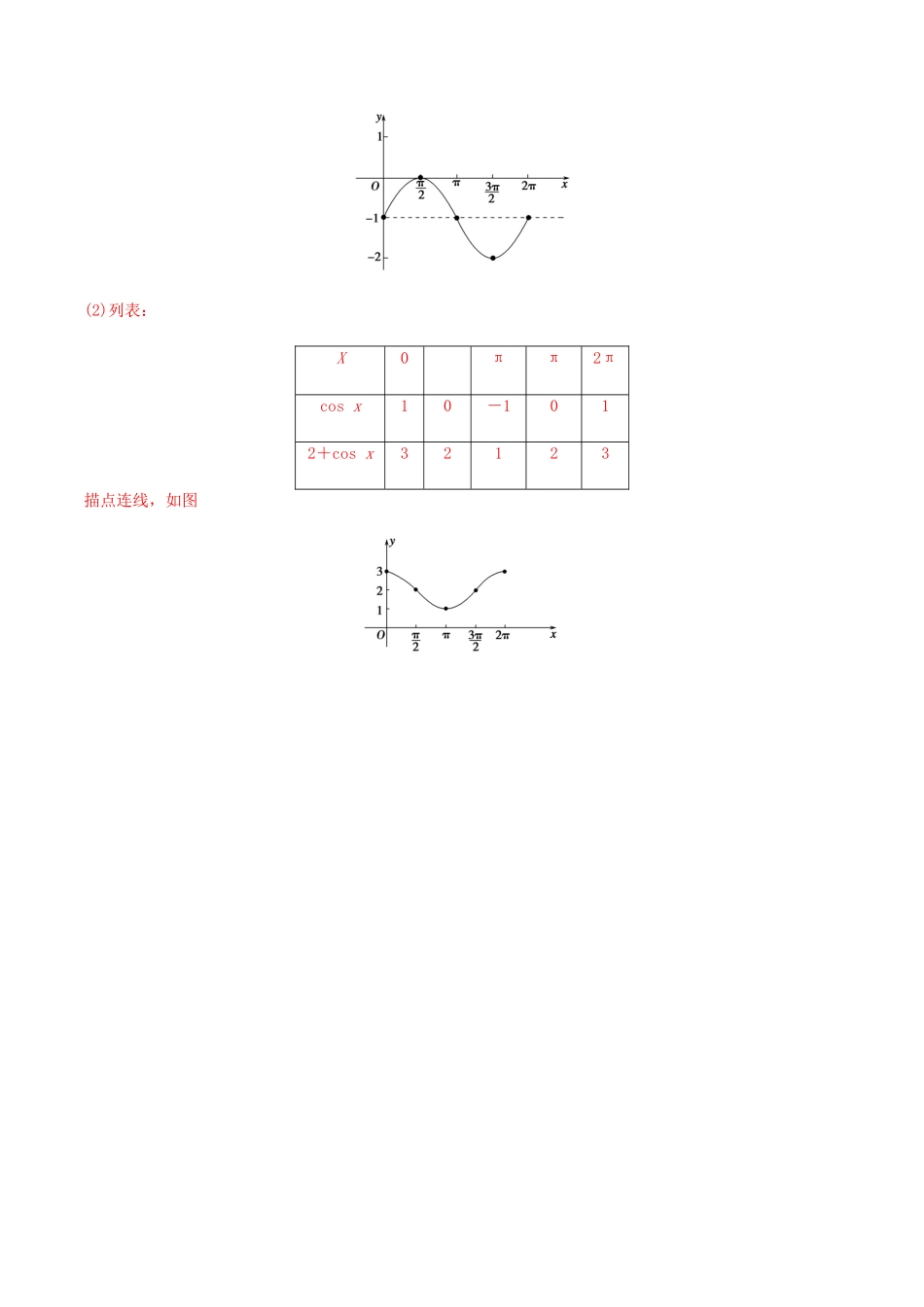
第五讲三角函数的性质一.正弦函数、余弦函数、正切函数的图象和性质函数y=sinxy=cosxy=tanx图像定义域RR{x|x≠+kπ,k∈Z}值域[-1,1][-1,1]R单调性在[2kπ-,2kπ+](k∈Z)上单调递增;在[2kπ+,2kπ+](k∈Z)上单调递减在[2kπ-π,2kπ](k∈Z)上单调递增;在[2kπ,2kπ+π](k∈Z)上单调递减在(kπ-,kπ+)(k∈Z)上单调递增最值x=2kπ+(k∈Z)时,ymax=1;x=2kπ-(k∈Z)时,ymin=-1x=2kπ(k∈Z)时,ymax=1;x=2kπ+π(k∈Z)时,ymin=-1无最值奇偶性奇函数偶函数奇函数对称性对称中心(kπ,0)(k∈Z)对称中心(kπ+,0)(k∈Z)对称中心(,0)(k∈Z)【套路秘籍】---千里之行始于足下对称轴l:x=kπ+(k∈Z)对称轴l:x=kπ(k∈Z)最小正周期2π2ππ二.用五点法作正弦函数和余弦函数的简图(1)在正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0),,(π,0),,(2π,0).(2)在余弦函数y=cosx,x∈[0,2π]的图象中,五个关键点是:(0,1),,(π,-1),,(2π,1).【修炼套路】---为君聊赋《今日诗》,努力请从今日始考向一“五点法”作正、余弦函数的图象【例1】用“五点法”作出下列函数的简图.(1)y=sinx-1,x∈[0,2π];(2)y=2+cosx,x∈[0,2π].【答案】见解析【解析】(1)列表:x0ππ2πsinx010-10sinx-1-10-1-2-1描点连线,如图(2)列表:X0ππ2πcosx10-1012+cosx32123描点连线,如图【套路总结】用“五点法”作函数y=Asin(ωx+φ)图象的步骤第一步:列表.ωx+φ0π2πx-----y0A0-A0第二步:在同一坐标系中描出各点.【举一反三】1.用“五点法”作出函数y=2-sinx,x∈[0,2π]的图象.【答案】见解析【解析】列表如下:x0π2πsinx010-102-sinx21232描点并将它们用光滑的曲线连接起来,如图所示.2.y=|sinx|,x∈[0,4π].【答案】见解析【解析】作y=sinx,x∈[0,4π]的图象,并将x轴下方的部分翻转到x轴上方(原x轴上方的部分不变),得y=|sinx|的图象(如图②所示).考向二周期【例2】求下列三角函数的周期:(1)y=cos2x,x∈R;(2)y=sin,x∈R;(3)y=|cosx|,x∈R.(4)y=cos|x|.【答案】(1)π(2)6π(3)π(4)2π【解析】(1)因为cos2(x+π)=cos(2x+2π)=cos2x,由周期函数的定义知,y=cos2x的周期为π.(2)因为sin=sin=sin,由周期函数的定义知,y=sin的周期为6π.(3)y=|cosx|的图象如图(实线部分)所示,由图象可知,y=|cosx|的周期为π.(4)由于函数y=cosx为偶函数,所以y=cos|x|=cosx,从而函数y=cos|x|与y=cosx的图象一样,因此最小正周期相同,为2π【套路总结】求三角函数最小正周期的常用方法(1)公式法,将函数化为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式,再利用T=求得;y=Atan(ωx+φ)+B,【举一反三】1.已知函数f(x)=cos(ω>0)的最小正周期为4,则ω=________.【答案】【解析】f(x)=cos(ω>0),由周期计算公式,可得T==4,解得ω=.2.若函数f(x)=sin(ω>0)的最小正周期为π,则f的值是________.【答案】【解析】由题意,得=π,所以ω=2,f(x)=sin.因此f=sin=sin=.3.函数的最小正周期为()A.B.C.D.【答案】A【解析】由,可得:,,所以本题选A。考向三单调性【例3】(1)函数f(x)=tan的单调递增区间是____________.(2)已知函数f(x)=2sin,则函数f(x)的单调递减区间为_______________(3)函数y=sinx+cosx的单调递增区间是____________.(4)已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是______【答案】(1)(k∈Z)(2)(k∈Z)(3)(4)【解析】(1)由kπ-<2x+0,得+<ωx+<ωπ+,又y=sinx的单调递减区间为,k∈Z,所以k∈Z,解得4k+≤ω≤2k+,k∈Z.又由4k+-≤0,k∈Z且2k...