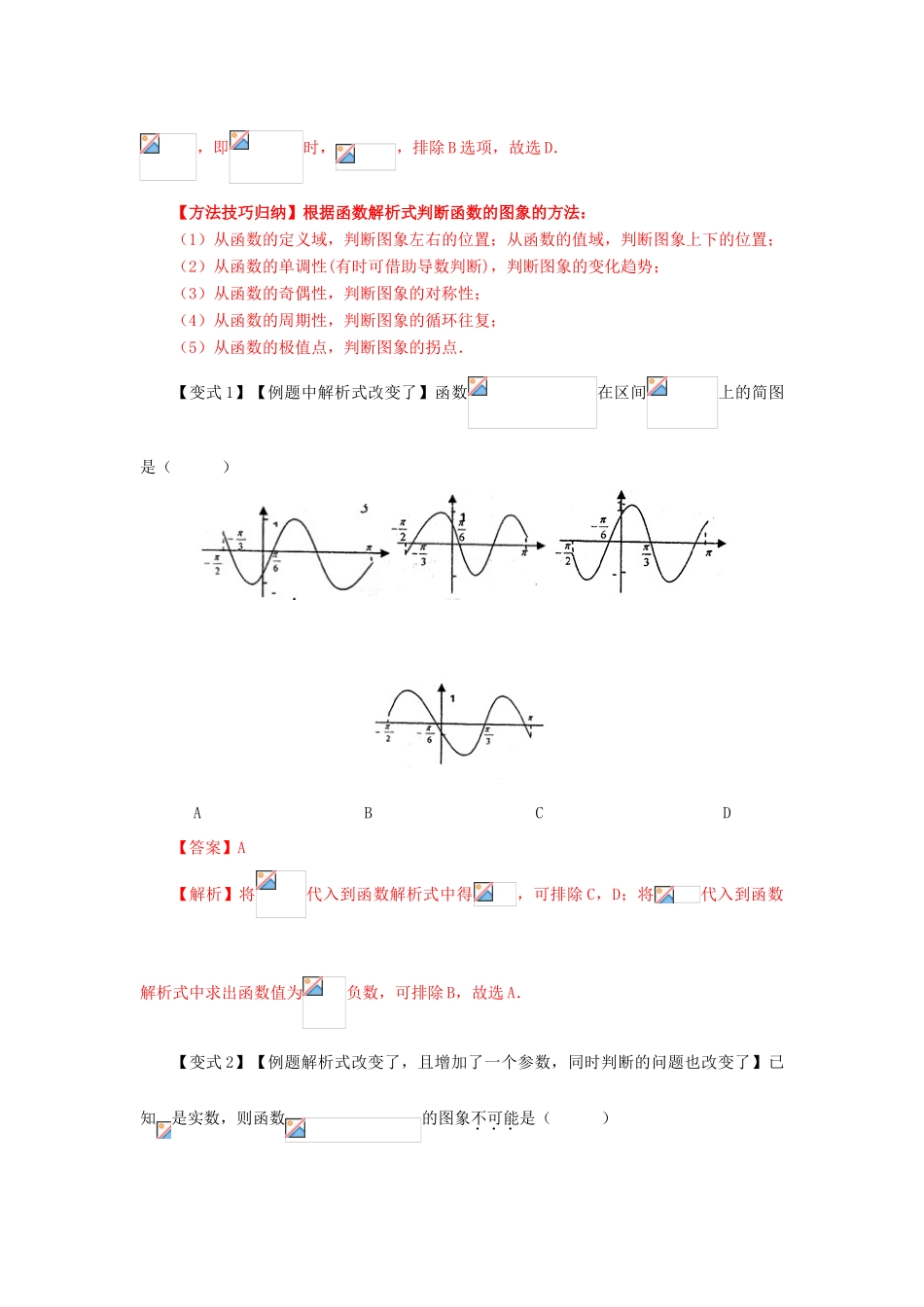
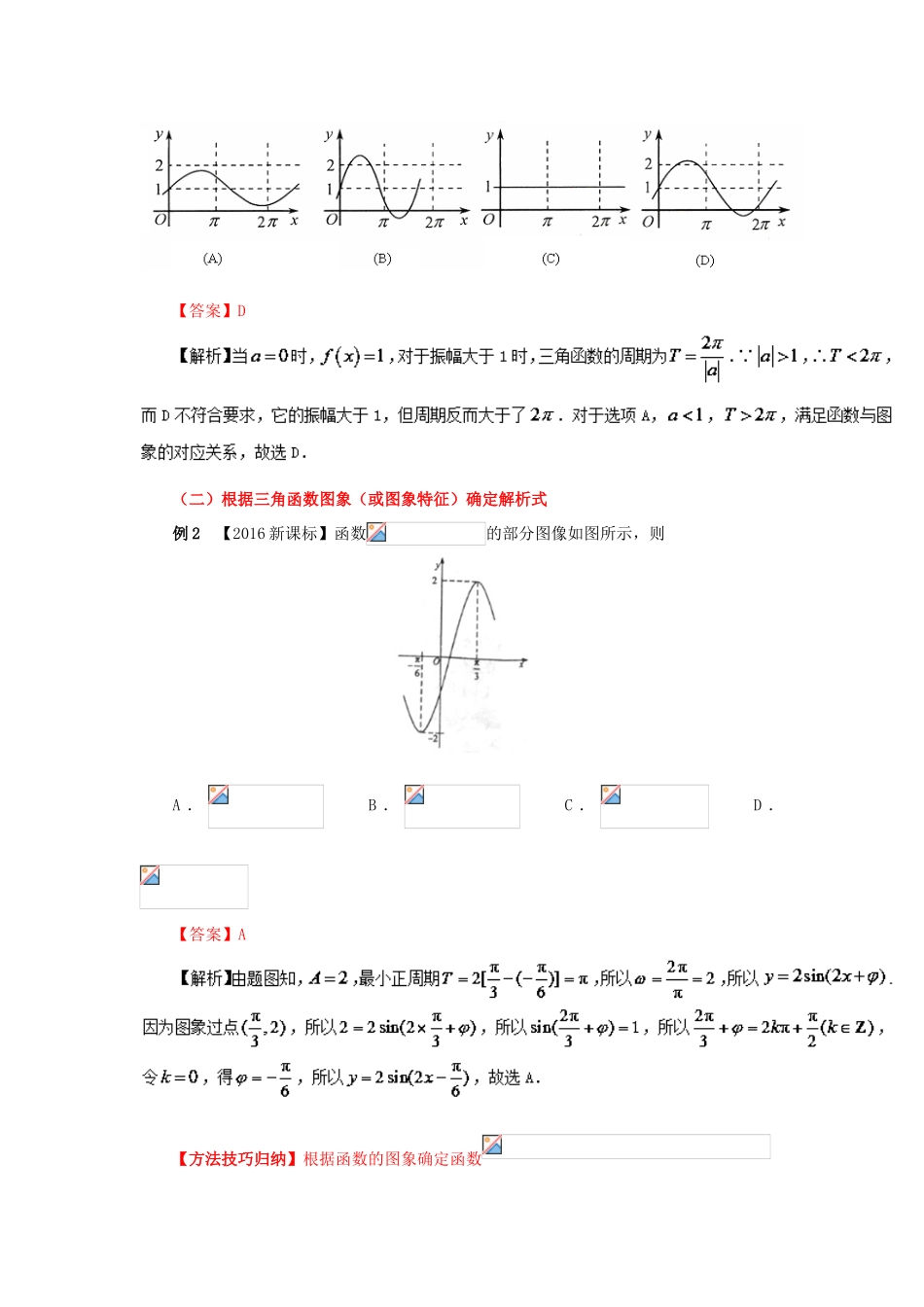
考点16:三角函数的图象与应用【考纲要求】(1)能画出,,的图像;(2)了解函数的物理意义;能画出的图像,了解参数对函数图像变化的影响;(3)了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题.【命题规律】三角函数的图象是高考考查的重点和热点内容,主要从以下两个方面进行考查:(1)三角函数图象变换问题以及由图象确定解析式问题,主要以选择题、填空题的形式考查;(2)利用三角函数的图象求解与三角函数有关的函数的零点、方程的根、图象的交点等问题,通常以选择题与填空题形式考查.预计2018年高考对三角函数图象的考查也主要体现在函数图象的识别与应用,会以客观题出现.【典型高考试题变式】(一)根据三角函数图象(或图象特征)确定解析式例1【2016浙江】函数的图象是()【答案】D【解析】因为为偶函数,所以它的图象关于轴对称,排除A、C选项;当,即时,,排除B选项,故选D.【方法技巧归纳】根据函数解析式判断函数的图象的方法:(1)从函数的定义域,判断图象左右的位置;从函数的值域,判断图象上下的位置;(2)从函数的单调性(有时可借助导数判断),判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的周期性,判断图象的循环往复;(5)从函数的极值点,判断图象的拐点.【变式1】【例题中解析式改变了】函数在区间上的简图是()ABCD【答案】A【解析】将代入到函数解析式中得,可排除C,D;将代入到函数解析式中求出函数值为负数,可排除B,故选A.【变式2】【例题解析式改变了,且增加了一个参数,同时判断的问题也改变了】已知是实数,则函数的图象不可能是()【答案】D(二)根据三角函数图象(或图象特征)确定解析式例2【2016新课标】函数的部分图像如图所示,则A.B.C.D.【答案】A【方法技巧归纳】根据函数的图象确定函数中的参数主要方法:(1),主要是根据图象的最高点或最低点的纵坐标确定,即,;(2)的值主要由周期的值确定,而的值的确定主要是根据图象的零点与最值点的横坐标确定;(3)值的确定主要是由图象的特殊点(通常优先取非零点)的坐标确定.【变式1】【例题给出的方式没有改变,解析式中增加了一个参数】如图所示,某地一天6~14时的温度变化曲线近似满足函数,则这段曲线的函数解析式可以为()A.,B.,C.,D.,【答案】A【变式2】【例题由直接给出图象改为由描述性给出图象特征,所求也适当有变化】若以函数的图象中相邻三个最值点为顶点的三角形是面积为1的直角三角形,则的值为()A.1B.2C.D.【答案】C【解析】如图所示,由题意可得:,∴,则,,故选C.(三)三角函数图象的变换例3【2017新课标1】已知曲线:,:,则下面结论正确的是()A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线【答案】D【方法技巧归纳】在进行三角函数图象变换时,提倡“先平移,后伸缩”,但“先伸缩,后平移”也经常出现在题目中,所以也必须熟练掌握,无论是哪种变形,切记每一个变换总是对字母而言,即图象变换要看“变量”起多大变化,而不是“角”变化多少.“先平移,后伸缩”主要体现为由函数平移得到函数的图象时,平移个长度单位;“先伸缩,后平移”主要体现为由函数平移得到函数的图象时,平移个长度单位.【变式1】【由例题确定平移过程改为了确定平移后的函数解析式】把函数的图象向左平移个单位,然后把图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),则所得图形对应的函数解析式为()A.B.C.D.【答案】B【解析】把函数的图象向左平移个单位,得到函数的图象,再把图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),得到,故选B.【变式2】【例题中的一个函数的解析式改变为较复杂的解析式,变...