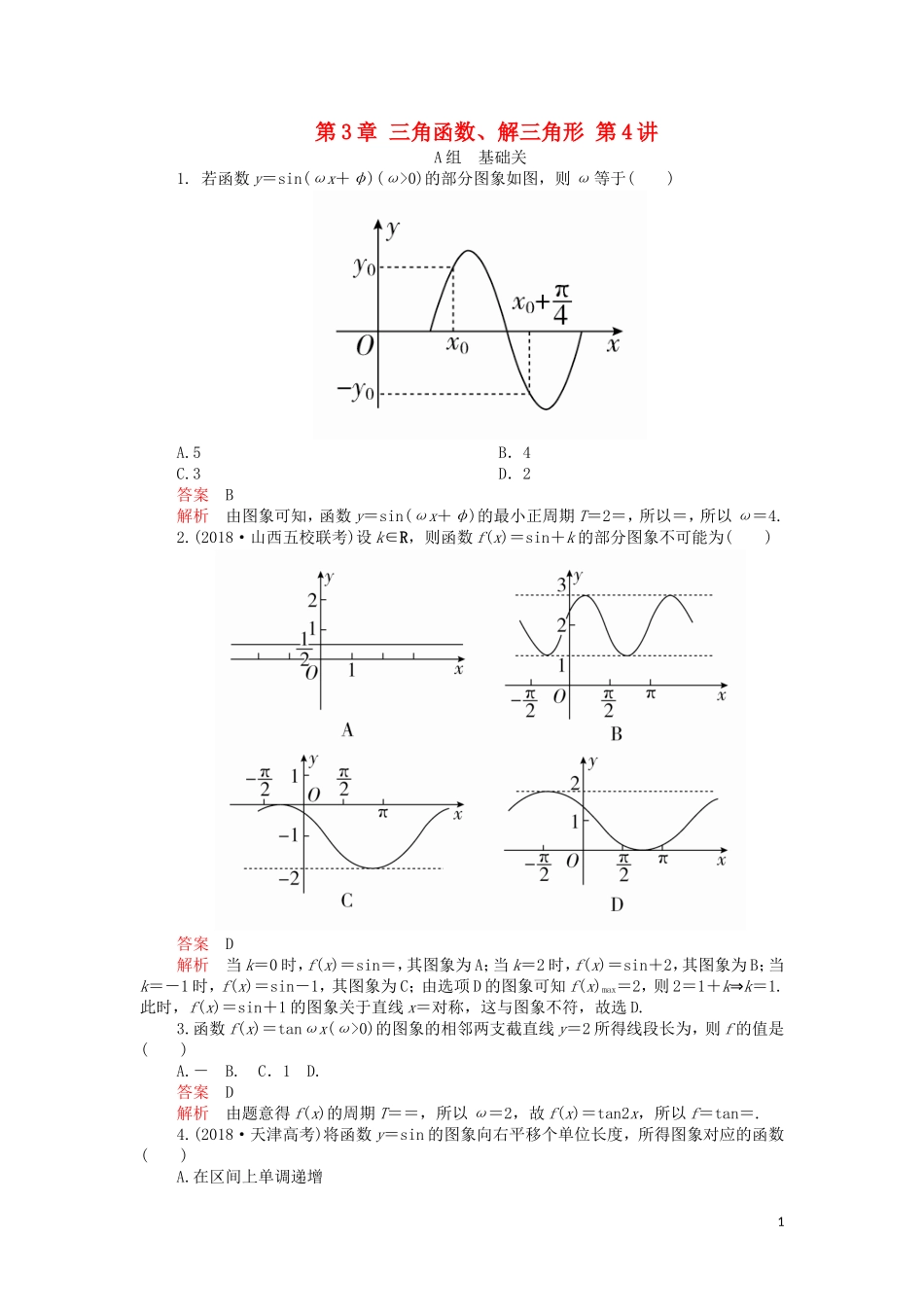
第3章三角函数、解三角形第4讲A组基础关1.若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω等于()A.5B.4C.3D.2答案B解析由图象可知,函数y=sin(ωx+φ)的最小正周期T=2=,所以=,所以ω=4.2.(2018·山西五校联考)设k∈R,则函数f(x)=sin+k的部分图象不可能为()答案D解析当k=0时,f(x)=sin=,其图象为A;当k=2时,f(x)=sin+2,其图象为B;当k=-1时,f(x)=sin-1,其图象为C;由选项D的图象可知f(x)max=2,则2=1+k⇒k=1.此时,f(x)=sin+1的图象关于直线x=对称,这与图象不符,故选D.3.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=2所得线段长为,则f的值是()A.-B.C.1D.答案D解析由题意得f(x)的周期T==,所以ω=2,故f(x)=tan2x,所以f=tan=.4.(2018·天津高考)将函数y=sin的图象向右平移个单位长度,所得图象对应的函数()A.在区间上单调递增1B.在区间上单调递减C.在区间上单调递增D.在区间上单调递减答案A解析因为将函数y=sin的图象向右平移个单位长度,得到函数y=sin2x的图象.用五点法作出草图,如图,从图中可以看出A正确,其他都不正确.5.(2018·西安八校联考)已知函数f(x)=sin(ωx+φ)的图象上的一个最高点和它相邻的一个最低点的距离为2,且函数f(x)的图象过点P,则函数f(x)=()A.sinB.sinC.sinD.sin答案A解析由题意得=2,解得ω=,所以函数f(x)=sin,又因为函数f(x)的图象过点P,所以sin(π+φ)=-,即-sinφ=-,sinφ=,又因为|φ|<,所以φ=,所以f(x)=sin.6.(2018·合肥模拟)已知函数f(x)=sin的图象向右平移个单位长度后,所得的图象关于y轴对称,则ω的最小正值为()A.1B.2C.3D.4答案B解析将函数f(x)=sin的图象向右平移个单位长度后得到函数g(x)=sin的图象,因为函数g(x)的图象关于y轴对称,所以-+=kπ+(k∈Z),易知当k=-1时,ω取最小正值2,故选B.7.(2018·枣庄二模)将函数f(x)=2sin的图象向左平移个单位,再把所有点的横坐标伸长到原来的2倍,得到函数y=g(x)的图象,则下列关于函数y=g(x)的说法错误的是()A.最小正周期为πB.图象关于直线x=对称C.图象关于点对称D.初相为答案C解析易求得g(x)=2sin,其最小正周期为π,初相为,即A,D正确;而g=2sin=2,故函数y=g(x)的图象关于直线x=对称,即B正确,C错误,选C.8.已知函数f(x)=sin(ωx+φ)的部分图象如图所示,又x1,x2∈,且f(x1)=f(x2),则f(x1+x2)=________.答案2解析由题图可知,=-=,则T=π,ω=2,又=,所以f(x)的图象过点,即sin=1,又|φ|<,可得φ=,所以f(x)=sin.由f(x1)=f(x2),x1,x2∈,可得x1+x2=-+=,所以f(x1+x2)=f=sin=sin=.9.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价9千元,9月份价格最低为5千元.则7月份的出厂价格为________元.答案6000解析作出函数简图如图:三角函数模型为y=Asin(ωx+φ)+B,由题意知,A=2000,B=7000,T=2×(9-3)=12,∴ω==.将(3,9000)看成函数图象的第二个特殊点,则有×3+φ=,∴φ=0,故f(x)=2000sinx+7000(1≤x≤12,x∈N*).∴f(7)=2000×sin+7000=6000.故7月份的出厂价格为6000元.10.方程sinπx=x的解的个数是________.答案7解析如图所示,在x≥0时,有4个交点,根据奇偶性,所以方程sinπx=x的解有7个.B组能力关1.(2019·昆明质检)已知函数f(x)=sin(0<ω<2)满足条件:f=0,为了得到函数y=f(x)的图象,可将函数g(x)=cosωx的图象向右平移m(m>0)个单位长度,则m的最小值为()A.1B.C.D.3答案A解析由题意,得sin=0,即-ω+=kπ(k∈Z),则ω=-2kπ(k∈Z),结合0<ω<2,得ω=,所以f(x)=sin=cos=cos,所以只需将函数g(x)=cosx的图象向右至少平移1个单位长度,即可得到函数y=f(x)的图象,故选A.2.(2018·哈尔滨六中模拟)设函数f(x)=sin,x∈,若方程f(x)=a恰好有三个根x1,x2,x3,且x1