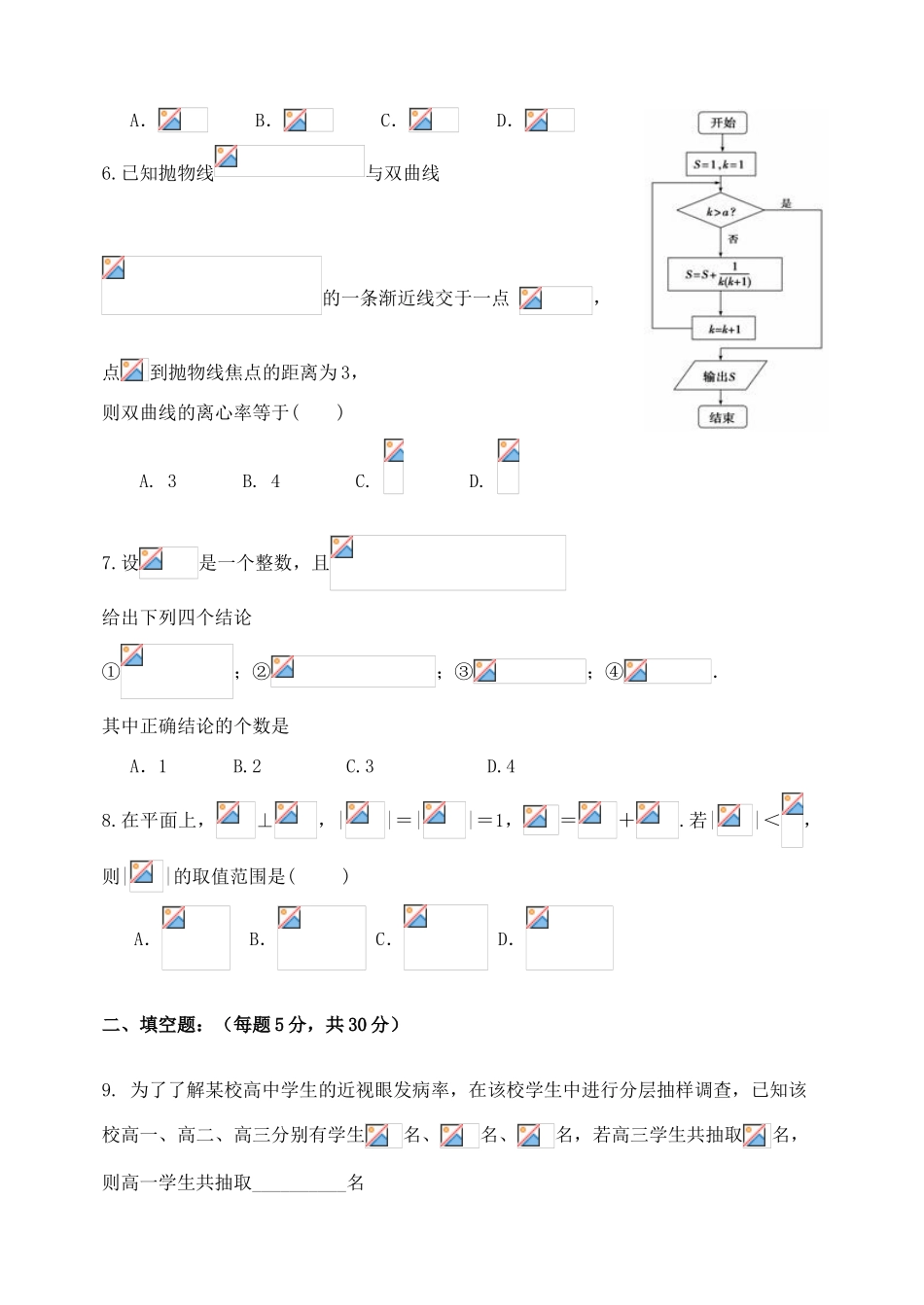
静海一中2014-2015第一学期高三数学(理)期末终结性检测试卷考生注意:1.本试卷分第Ⅰ卷基础题(122分)和第Ⅱ卷提高题(28分)两部分,共150分。2.试卷书写规范工整,卷面整洁清楚,酌情加减1-2分,并计入总分。知识技能学习能力习惯养成总分内容函数、导数解析几何数列立体分类讨论化归思想卷面整洁15030254727211-2分第I卷基础题(共122分)一、选择题(每题5分,共40分)1.设是虚数单位,复数,其共轭复数的虚部是()A.B.C.-D.2.若变量满足约束条件,则的最小值是()A.B.0C.D.3.若的展开式中项的系数为()A.14B.-14C.280D.-2804.已知某几何体的三视图如图,其中正(主)视图中半圆半径为1,则该几何体体积为()A.B.C.D.5.某程序框图如图所示,若该程序运行后输出的值是,则()A.B.C.D.6.已知抛物线与双曲线的一条渐近线交于一点,点到抛物线焦点的距离为3,则双曲线的离心率等于()A.3B.4C.D.7.设是一个整数,且给出下列四个结论①;②;③;④.其中正确结论的个数是A.1B.2C.3D.48.在平面上,⊥,||=||=1,=+.若||<,则||的取值范围是()A.B.C.D.二、填空题:(每题5分,共30分)9.为了了解某校高中学生的近视眼发病率,在该校学生中进行分层抽样调查,已知该校高一、高二、高三分别有学生名、名、名,若高三学生共抽取名,则高一学生共抽取__________名PADBCO·10.集合,,若“”是“”的充分条件,则的取值范围是.11.若实数,则的最小值为__________.12.已知直线的参数方程和圆的极坐标方程,则直线与圆C相交所得的弦长为________.13.如图已知切⊙O于点,D为的中点,过点引割线交⊙O于、两点.,,,则.14.已知函数若函数恰有4个零点,则实数的取值范围为_________.三、解答题:15.(13分)已知函数(1)(4分)求函数的最大值,并写出取最大值时的取值集合;(2)(4分)若,求的值;(3)(5分)在中,角的对边分别为,若,求的最小值.16.(13分)某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,,(495,,……(510,,由此得到样本的频率分布直方图,如图4所示.(1)(3分)根据频率分布直方图,求重量不超过500克的产品数量;(2)(7分)在上述抽取的40件产品中任取2件,设Y为重量不超过500克的产品数量,求Y的分布列及期望;(3)(3分)从流水线上任取5件产品,求恰有2件产品合格的重量不超过500克的概率.17.(13分)如图,是边长为3的正方形,,,,与平面所成角为.(1)(4分)求证:;(2)(5分)求二面角的余弦值;(3)(4分)设点是线段上一个动点,试确定点的位置,使得,并证明你的结论.18.(13分)已知椭圆C的中心在原点,离心率等于,它的一个短轴端点点恰好是抛物线的焦点.(1)(3分)求椭圆C的方程;(2)已知、是椭圆上的两点,,是椭圆上位于直线两侧的动点.①(4分)若直线的斜率为,求四边形面积的最大值;②(6分)当,运动时,满足直线、与轴始终围成一个等腰三角形,试问直线的斜率是否为定值,请说明理由.第Ⅱ卷提高题(共28分)19.(14分)已知正项数列的前项和为,且满足.(1)(4分)求数列的通项公式;(2)(4分)设,数列满足,求数列的通项公式;(3)(6分)设,求证:.20.(14分)设函数(1)(4分)当时,求函数的最大值;(2)(4分)令,其图象上任意一点处切线的斜率恒成立,求实数的取值范围;(3)(6分)当,方程有唯一实数解,求正数的值.静海一中2014-2015第一学期高三数学(理)期末终结性检测试卷答题纸得分框知识与技能学法题卷面整洁总分第Ⅰ卷基础题(共122分)一、选择题(每题5分,共40分)题号12345678答案二、填空题(每题5分,共30分)9.___10.11.12.13.14.三、解答题(本大题共4题,共52分)15.(13分)16.(13分)17(13分)18.(13分)第Ⅱ卷提高题(共28分)19.(14分)20.(14分)答案:题号12345678答案CBBDAAAD9、4010、(-2,2)11、12、13、414、(1,3)15解:(Ⅰ).∴函数的最大值为.当取最大值时,解得.故的取值集合为.(2)略(3)由题意,化简得,,∴,∴在中,根据余弦定理,得.由,知,即.∴当时,取最小值.16.解:(...