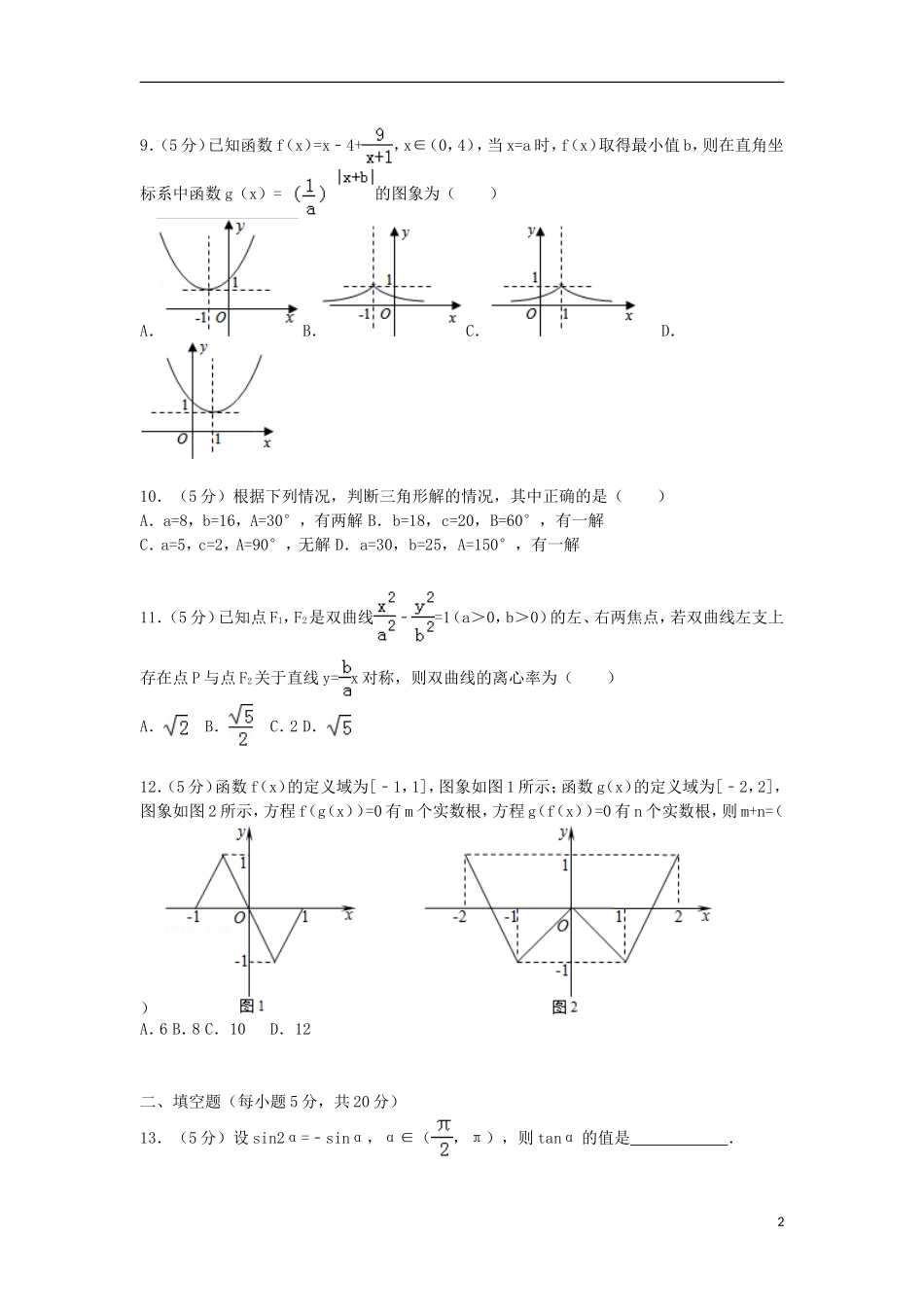
湖北省孝感高中2015-2016学年高三(上)9月调考数学试卷(文科)一、选择题(每小题5分,共60分.)1.(5分)函数f(x)=﹣lg(x﹣1)的定义域是()A.[2,+∞)B.(﹣∞,2)C.(1,2]D.(1,+∞)2.(5分)设集合A={x|1≤x≤2},B={y|1≤y≤4},则下述对应法则f中,不能构成A到B的映射的是()A.f:x→y=x2B.f:x→y=3x﹣2C.f:x→y=﹣x+4D.f:x→y=4﹣x23.(5分)下列有关命题的说法错误的是()A.命题“若x2﹣3x+2=0则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”B.“x=1”是“x2﹣3x+2=0”的充分不必要条件C.若p∧q为假命题,则p、q均为假命题D.对于命题p:∃x∈R,使得x2+x+1<0.则¬p:∀x∈R,均有x2+x+1≥04.(5分)已知a是函数f(x)=2x﹣x的零点,若0<x0<a,则f(x0)的值满足()A.f(x0)=0B.f(x0)>0C.f(x0)<0D.f(x0)的符号不确定5.(5分)函数f(x)=x2﹣4x+5在区间[0,m]上的最大值为5,最小值为1,则m的取值范围是()A.[2,+∞)B.[2,4]C.(﹣∞,2]D.[0,2]6.(5分)将函数y=sin(2x﹣)图象向左平移个单位,所得函数图象的一条对称轴的方程是()A.x=B.x=C.x=D.x=﹣7.(5分)比较a=2﹣3.1,b=0.53,c=log3.14,则a,b,c的大小关系是()A.c<b<aB.b<c<aC.a<c<bD.a<b<c8.(5分)已知奇函数f(x)在区间[0,+∞)上是单调递增函数,则满足f(2x﹣1)<f()的x的取值范围是()A.(﹣∞,)B.[,)C.(,)D.[,)19.(5分)已知函数f(x)=x﹣4+,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)=的图象为()A.B.C.D.10.(5分)根据下列情况,判断三角形解的情况,其中正确的是()A.a=8,b=16,A=30°,有两解B.b=18,c=20,B=60°,有一解C.a=5,c=2,A=90°,无解D.a=30,b=25,A=150°,有一解11.(5分)已知点F1,F2是双曲线﹣=1(a>0,b>0)的左、右两焦点,若双曲线左支上存在点P与点F2关于直线y=x对称,则双曲线的离心率为()A.B.C.2D.12.(5分)函数f(x)的定义域为[﹣1,1],图象如图1所示;函数g(x)的定义域为[﹣2,2],图象如图2所示,方程f(g(x))=0有m个实数根,方程g(f(x))=0有n个实数根,则m+n=()A.6B.8C.10D.12二、填空题(每小题5分,共20分)13.(5分)设sin2α=﹣sinα,α∈(,π),则tanα的值是.214.(5分)已知函数f(x)=,若f(4)>1,则实数a的取值范围是.15.(5分)若函数f(x)=x2﹣ex﹣ax在R上存在单调递增区间,则实数a的最大值为.16.(5分)设A为非空实数集,若∀x,y∈A,都有x+y,x﹣y,xy∈A,则称A为封闭集.①集合A={﹣2,﹣1,0,1,2}为封闭集;②集合A={n|n=2k,k∈Z}为封闭集;③若集合A1,A2为封闭集,则A1∪A2为封闭集;④若A为封闭集,则一定有0∈A.其中正确结论的序号是.三、解答题(解答应写出文字说明、证明过程或演算步骤)17.(10分)已知A={x|﹣1<x≤3},B={x|m≤x<1+3m}(1)当m=1时,求A∪B;(2)若B⊆∁RA,求实数m的取值范围.18.(12分)在△ABC中,a、b、c分别为角A、B、C的对边,4sin2﹣cos2C=(1)求角C;(2)若边c=,a+b=3,求边a和b的值.19.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象如图所示.(1)求函数的解析式;(2)设0<x<π,且方程f(x)=m有两个不同的实数根,求实数m的取值范围和这两个根的和.20.(12分)定义在实数集上的函数f(x)=x2+x,g(x)=x3﹣2x+m.(1)求函数f(x)的图象在x=1处的切线方程;(2)若f(x)≥g(x)对任意的x∈[﹣4,4]恒成立,求实数m的取值范围.321.(12分)据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).(1)当t=4时,求s的值;(2)将s随t变化的规律用数学关系式表示出来;(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发...