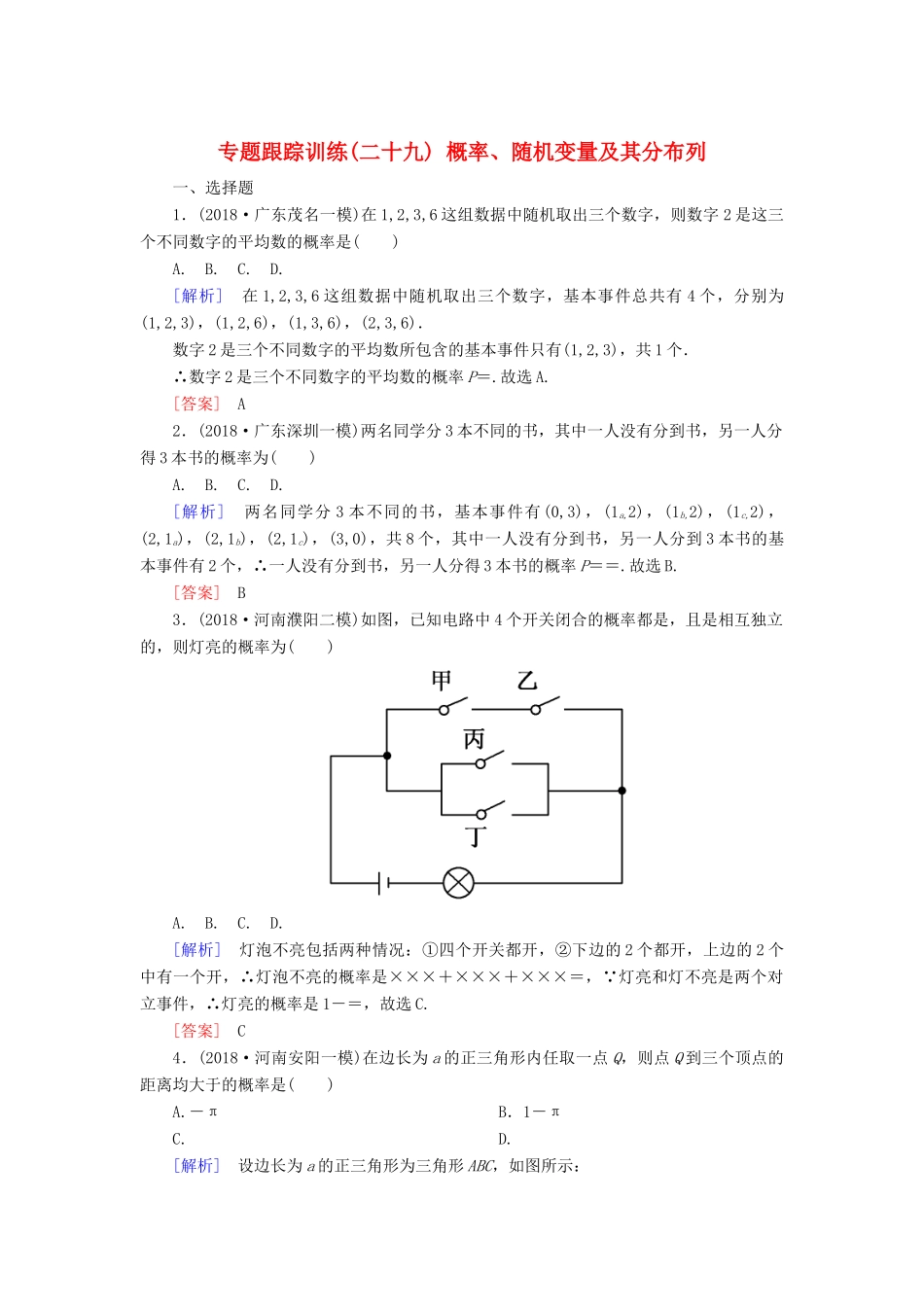
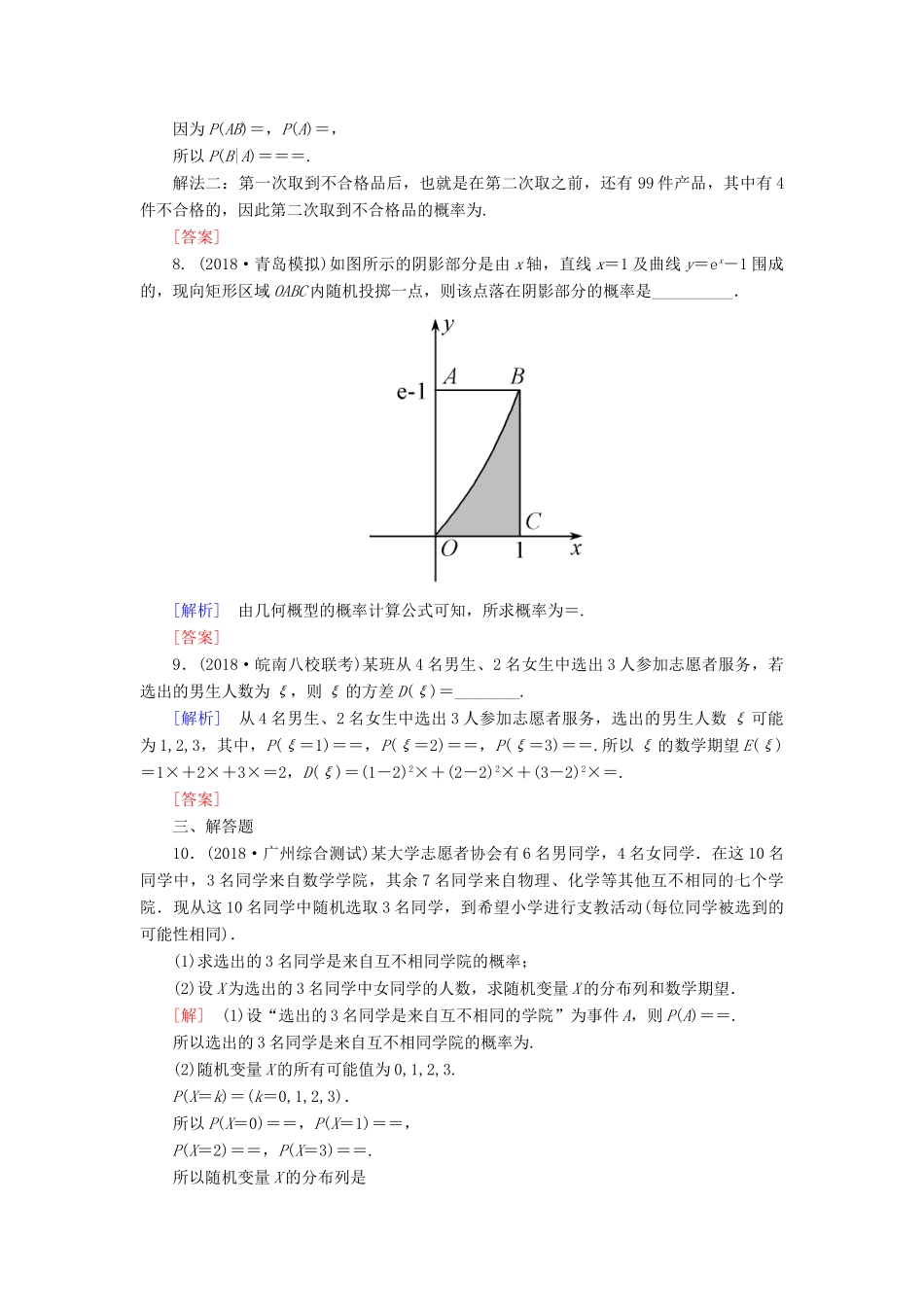
专题跟踪训练(二十九)概率、随机变量及其分布列一、选择题1.(2018·广东茂名一模)在1,2,3,6这组数据中随机取出三个数字,则数字2是这三个不同数字的平均数的概率是()A.B.C.D.[解析]在1,2,3,6这组数据中随机取出三个数字,基本事件总共有4个,分别为(1,2,3),(1,2,6),(1,3,6),(2,3,6).数字2是三个不同数字的平均数所包含的基本事件只有(1,2,3),共1个.∴数字2是三个不同数字的平均数的概率P=.故选A.[答案]A2.(2018·广东深圳一模)两名同学分3本不同的书,其中一人没有分到书,另一人分得3本书的概率为()A.B.C.D.[解析]两名同学分3本不同的书,基本事件有(0,3),(1a,2),(1b,2),(1c,2),(2,1a),(2,1b),(2,1c),(3,0),共8个,其中一人没有分到书,另一人分到3本书的基本事件有2个,∴一人没有分到书,另一人分得3本书的概率P==.故选B.[答案]B3.(2018·河南濮阳二模)如图,已知电路中4个开关闭合的概率都是,且是相互独立的,则灯亮的概率为()A.B.C.D.[解析]灯泡不亮包括两种情况:①四个开关都开,②下边的2个都开,上边的2个中有一个开,∴灯泡不亮的概率是×××+×××+×××=, 灯亮和灯不亮是两个对立事件,∴灯亮的概率是1-=,故选C.[答案]C4.(2018·河南安阳一模)在边长为a的正三角形内任取一点Q,则点Q到三个顶点的距离均大于的概率是()A.-πB.1-πC.D.[解析]设边长为a的正三角形为三角形ABC,如图所示: AB=a,∴S三角形ABC=·a2·sin=a2,满足到正三角形ABC的顶点A、B、C的距离至少有一个小于或等于的所有点组成的平面区域如图中阴影部分所示,各部分组合起来构成一个半径为的半圆,∴S阴影=·π·2=,∴使点Q到三个顶点A、B、C的距离都大于的概率P=1-=1-π.故选B.[答案]B5.在1,2,3,4,5,6,7,8这组数据中,随机取出五个不同的数,则数字4是取出的五个不同数的中位数的概率为()A.B.C.D.[解析]设事件A为“数字4是取出的五个不同数的中位数”.“从八个数字中取出五个数字”的种数为n=C=C=56.对事件A,先考虑数字4在五个数的中间位置,再考虑分别从数字1,2,3和5,6,7,8中各取两个数字,则事件A包含的基本事件种数为m=CC=3×6=18.由古典概型的概率计算公式,得P(A)===.[答案]B6.(2018·重庆一中一模)将4个不同的小球装入4个不同的盒子,则在至少有一个盒子为空的条件下,恰好有两个盒子为空的概率是()A.B.C.D.[解析]根据题意,将4个不同的小球装入4个不同的盒子的放法为44=256.若没有空盒,有A=24(种)放法,有1个空盒的放法有CCA=144(种),有3个空盒的放法有C=4种,则至少有一个盒子为空的放法有256-24=232(种),故“至少有一个盒子为空”的概率p1=,恰好有两个盒子为空的放法有256-24-144-4=84(种),故“恰好有两个盒子为空”的概率p2=,则在至少有一个盒子为空的条件下,恰好有两个盒子为空的概率p==.故选A.[答案]A二、填空题7.在100件产品中有95件合格品,5件不合格品.现从中不放回地取两次,每次任取一件,则在第一次取到不合格品后,第二次取到不合格品的概率为________.[解析]解法一:设事件A为“第一次取到不合格品”,事件B为“第二次取到不合格品”,则所求的概率为P(B|A),因为P(AB)=,P(A)=,所以P(B|A)===.解法二:第一次取到不合格品后,也就是在第二次取之前,还有99件产品,其中有4件不合格的,因此第二次取到不合格品的概率为.[答案]8.(2018·青岛模拟)如图所示的阴影部分是由x轴,直线x=1及曲线y=ex-1围成的,现向矩形区域OABC内随机投掷一点,则该点落在阴影部分的概率是__________.[解析]由几何概型的概率计算公式可知,所求概率为=.[答案]9.(2018·皖南八校联考)某班从4名男生、2名女生中选出3人参加志愿者服务,若选出的男生人数为ξ,则ξ的方差D(ξ)=________.[解析]从4名男生、2名女生中选出3人参加志愿者服务,选出的男生人数ξ可能为1,2,3,其中,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==.所以ξ的数学期望E(ξ)=1×+2×+3×=2,D(ξ)=(1-2)2×+(2-2)2×+(3-2)2×=.[答案]三、解答题10.(2018·广州综合测试)某大学志愿者协会有6名男同学,4名女同学.在这10...