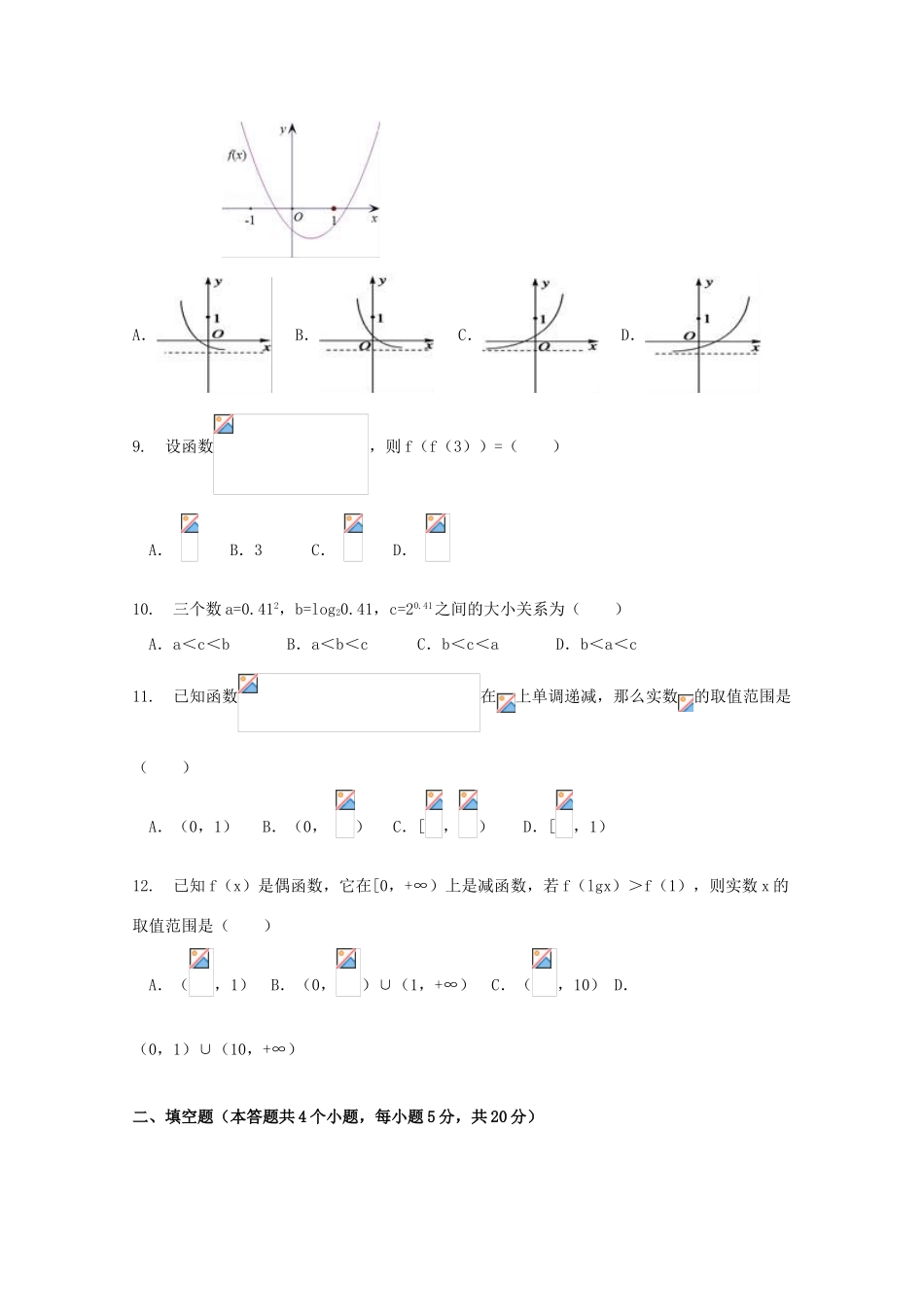
2017-2018学年度第一学期高一期中考试数学试卷注:卷面分值120分;时间:90分钟一、选择题(本答题共12个小题,每小题5分,共60分)1.如果集合A={x|x>﹣1},那么()A.0A⊆B.{0}∈AC.∈AD.{0}A⊆。2.设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则()A.{1,2}B.{3,4}C.{1}D.{2}3.若集合,,则集合的真子集的个数为()A.7B.8C.15D.164.下列各图中,不是函数图象的是()5.设集合A={y|y=2x,x∈R},B={x|x-1>0},则A∪B=()A.(﹣1,1)B.(0,1)C.D.(0,+∞)6.下列函数中,在区间(0,+∞)上单调递增且为偶函数的是()A.y=x3B.y=2xC.D.y=|x|7.函数y=x2﹣2tx+3在[1,+∞)上为增函数,则t的取值范围是()A.t≤1B.t≥1C.t≤﹣1D.t≥﹣18.已知函数(其中>)的图象如图所示,则函数的图象是()A.B.C.D.9.设函数,则f(f(3))=()A.B.3C.D.10.三个数a=0.412,b=log20.41,c=20.41之间的大小关系为()A.a<c<bB.a<b<cC.b<c<aD.b<a<c11.已知函数在上单调递减,那么实数的取值范围是()A.(0,1)B.(0,)C.[,)D.[,1)12.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则实数x的取值范围是()A.(,1)B.(0,)∪(1,+∞)C.(,10)D.(0,1)∪(10,+∞)二、填空题(本答题共4个小题,每小题5分,共20分)13.,则.14.函数y=ax+2(a>0,且a≠1)的图象经过的定点坐标是.15.已知,则函数f(x)的解析式为.16.已知y=f(x)是奇函数,若g(x)=f(x)+2且g(1)=1,则g(﹣1)=.三、解答题(本大题共4个小题,17题8分,18、19每小题10分,20题12分,共40分)17、(本小题满分8分)已知函数f(x)=lg(3+x)+lg(3﹣x).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性,并说明理由.18、(本小题满分10分)设全集U=R,集合A={y|﹣1<y<4},B={y|0<y<5},试求∁UB,A∪B,A∩B,A∩(∁UB),(∁UA)∩(∁UB).19、(本小题满分10分)已知函数y=4x﹣6×2x+8,求该函数的最小值,及取得最小值时x的值.20、(本小题满分12分)已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.(1)求f(x)的解析式;(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.2017-2018学年度第一学期高一期中考试数学试卷答案一、选择题:1.D、2.C、3.A、4.C、5.D、6.D、7.A、8.C、9.D、10.D、11.C、12.C二、填空题:13、1314、(﹣2,1)15、f(x)=x2﹣1,(x≥1)16、3三、解答题17.解:(1)要使函数有意义,则,解得﹣3<x<3,所以函数的定义域是(﹣3,3);(2)函数f(x)是偶函数,由(1)知函数的定义域关于原点对称,因为f(﹣x)=lg(3﹣x)+lg(3+x)=f(x),所以函数f(x)是偶函数.18.解:解:由条件得B={y|0<y<5},从而CUB={y|y≤0或y≥5},A∪B={y|﹣1<y<5},A∩B={y|0<y<4},A∩(CUB)={y|﹣1<y≤0},(CUA)∩(CUB)={y|y≤﹣1或y≥5}19.解:∵4x=(22)x=(2x)2则:y═(2x)-6(22)x+8∴令t=2x(t>0)则:函数y=t2﹣6t+8(t>0)显然二次函数,当t=3时有最小值.ymin=32﹣6×3+8=﹣1此时,t=3,即t=2x=3解得:x=答;当x=时,函数取得最小值﹣120、(1)∵函数f(x)是定义域为R上的奇函数,∴f(x)=﹣f(﹣x)又∵当x>0时,f(x)=x2+2x.若x>0,则﹣x<0.f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x∴f(x)=﹣f(﹣x)=2x﹣x2.∴f(x)=;(2)当x>0时,f(x)=x2+2x=(x+1)2﹣1,区间(0,+∞)在对称轴x=﹣1的右边,为增区间,由奇函数的性质,可得f(x)在R上递增.不等式f(t﹣2)+f(2t+1)>0即为f(1+2t)>﹣f(t﹣2)=f(2﹣t),即有1+2t>2﹣t,解得t>则t的取值范围是(,+∞).