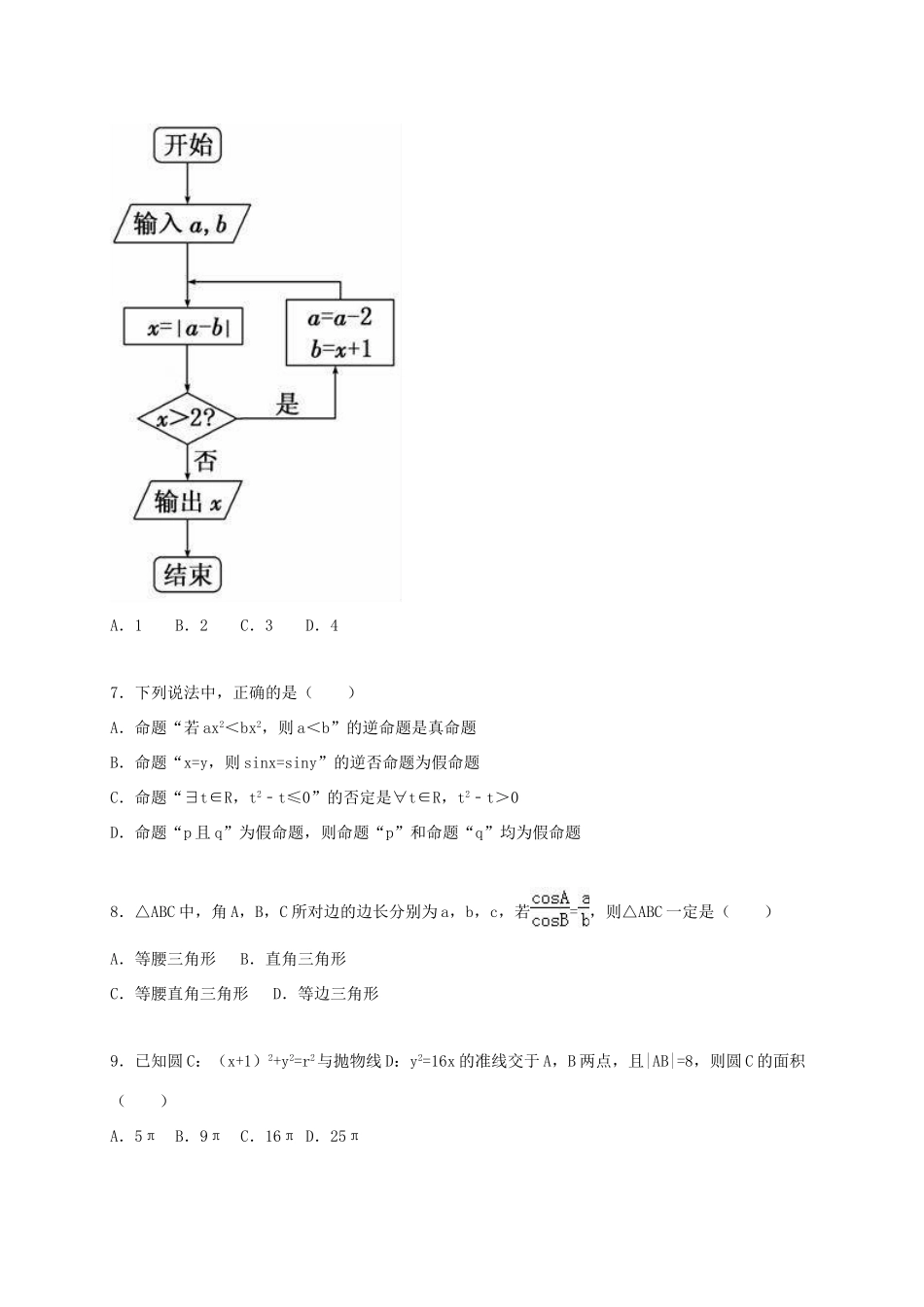
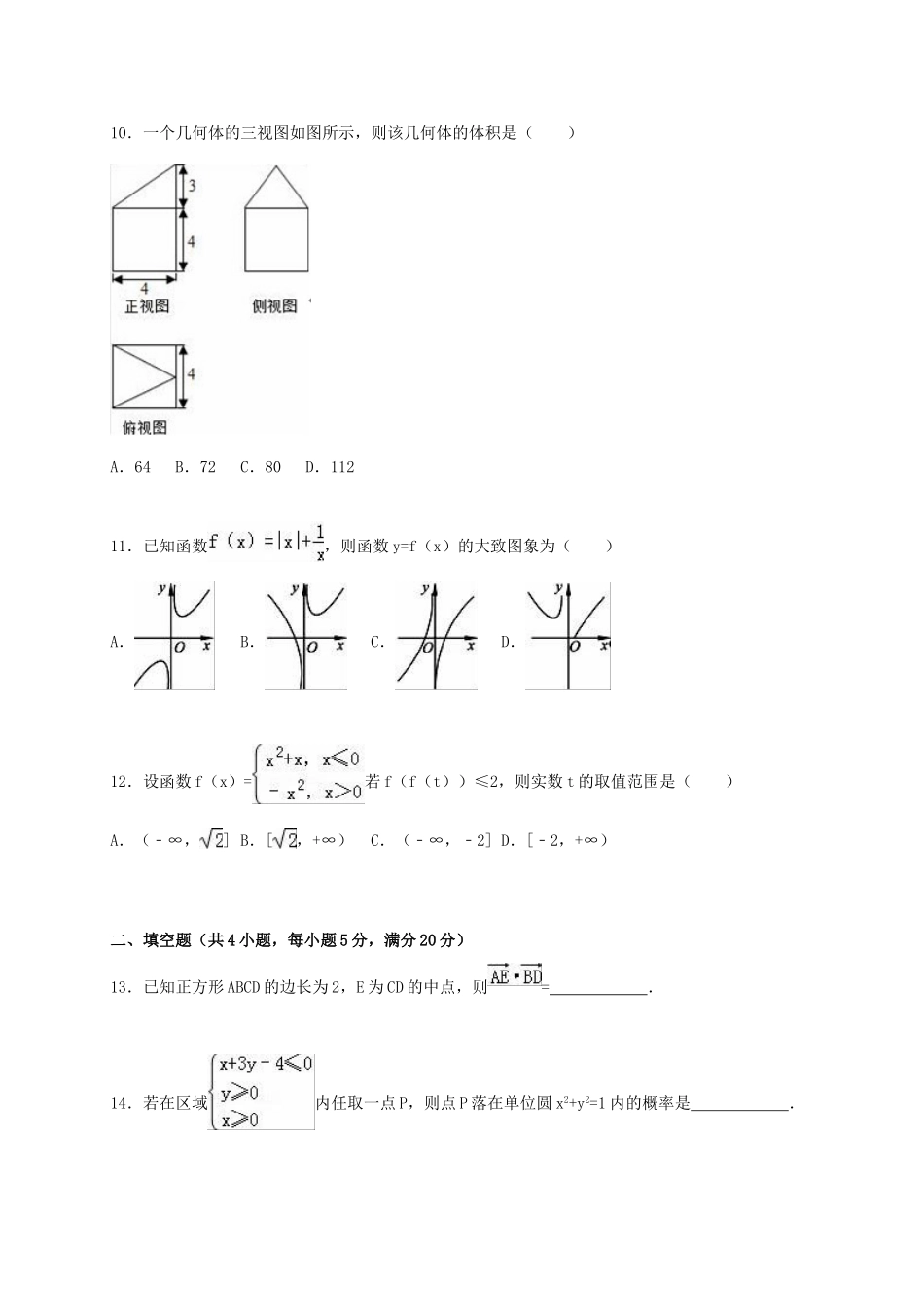
2015-2016学年广东省茂名市化州市高三(上)第一次模拟数学试卷(文科)一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项符合题目要求的)1.已知集合A={x|0≤x≤2},B={x|x<0或x>1},则A∩B=()A.(﹣∞,1]∪(2,+∞)B.(﹣∞,0)∪(1,2)C.(1,2]D.(1,2)2.已知i是虚数单位,则复数在复平面内所对应的点位于()A.第四象限B.第三象限C.第二象限D.第一象限3.已知等比数列{an}的公比q=2,且2a4,a6,48成等差数列,则{an}的前8项和为()A.127B.255C.511D.10234.既是偶函数又在区间(0,π)上单调递减的函数是()A.y=sinxB.y=cosxC.y=sin2xD.y=cos2x5.已知α∈(,π),sinα=,则tan(α﹣)=()A.﹣7B.﹣C.7D.6.阅读如图所示的程序框图.若输入a=6,b=1,则输出的结果是()A.1B.2C.3D.47.下列说法中,正确的是()A.命题“若ax2<bx2,则a<b”的逆命题是真命题B.命题“x=y,则sinx=siny”的逆否命题为假命题C.命题“∃t∈R,t2﹣t≤0”的否定是∀t∈R,t2﹣t>0D.命题“p且q”为假命题,则命题“p”和命题“q”均为假命题8.△ABC中,角A,B,C所对边的边长分别为a,b,c,若=,则△ABC一定是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形9.已知圆C:(x+1)2+y2=r2与抛物线D:y2=16x的准线交于A,B两点,且|AB|=8,则圆C的面积()A.5πB.9πC.16πD.25π10.一个几何体的三视图如图所示,则该几何体的体积是()A.64B.72C.80D.11211.已知函数,则函数y=f(x)的大致图象为()A.B.C.D.12.设函数f(x)=若f(f(t))≤2,则实数t的取值范围是()A.(﹣∞,]B.[,+∞)C.(﹣∞,﹣2]D.[﹣2,+∞)二、填空题(共4小题,每小题5分,满分20分)13.已知正方形ABCD的边长为2,E为CD的中点,则=.14.若在区域内任取一点P,则点P落在单位圆x2+y2=1内的概率是.15.直线y=3x+1是曲线y=x3﹣a的一条切线,则实数a的值为.16.设F1,F2是双曲线C:(a>0,b>0)的两个焦点.若在C上存在一点P.使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为.三、解答题(解答应写出文字说明,证明过程或演算步骤)共5小题,满分60分)17.已知各项都不相等的等差数列{an},a4=10,又a1,a2,a6成等比数列.(1)求数列{an}的通项公式;(2)设bn=2+2n,求数列{bn}的前n项和Sn.18.对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:分组频数频率[10,15)mP[15,20)24n[20,25)40.1[25,30)20.05合计M1(Ⅰ)求出表中M,p及图中a的值;(Ⅱ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,30)内的概率.19.如图,四棱P﹣ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.(1)求证:EF∥平面PCD;(2)求证:平面PBD⊥平面PAC.20.已知椭圆E的中心在坐标原点、对称轴为坐标轴,且抛物线的焦点是它的一个焦点,又点在该椭圆上.(1)求椭圆E的方程;(2)若斜率为直线l与椭圆E交于不同的两点B、C,当△ABC面积的最大值时,求直线l的方程.21.已知f(x)=xlnx,g(x)=x3+ax2﹣x+2(Ⅰ)求函数f(x)的单调区间;(Ⅱ)求函数f(x)在[t,t+2](t>0)上的最小值;(Ⅲ)对一切的x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.请考生在第22、23、24三题中任选一题作答【选修4-1:几何证明选讲】22.在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.(1)求证:;(2)若AC=3,求AP•AD的值.【选修4-4:坐标系与参数方程】23.(选修4﹣4:坐标系与参数方程)已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)【选修4-5:不等式选讲】24.设函数f(x)=|2x﹣1|﹣|x+2|...