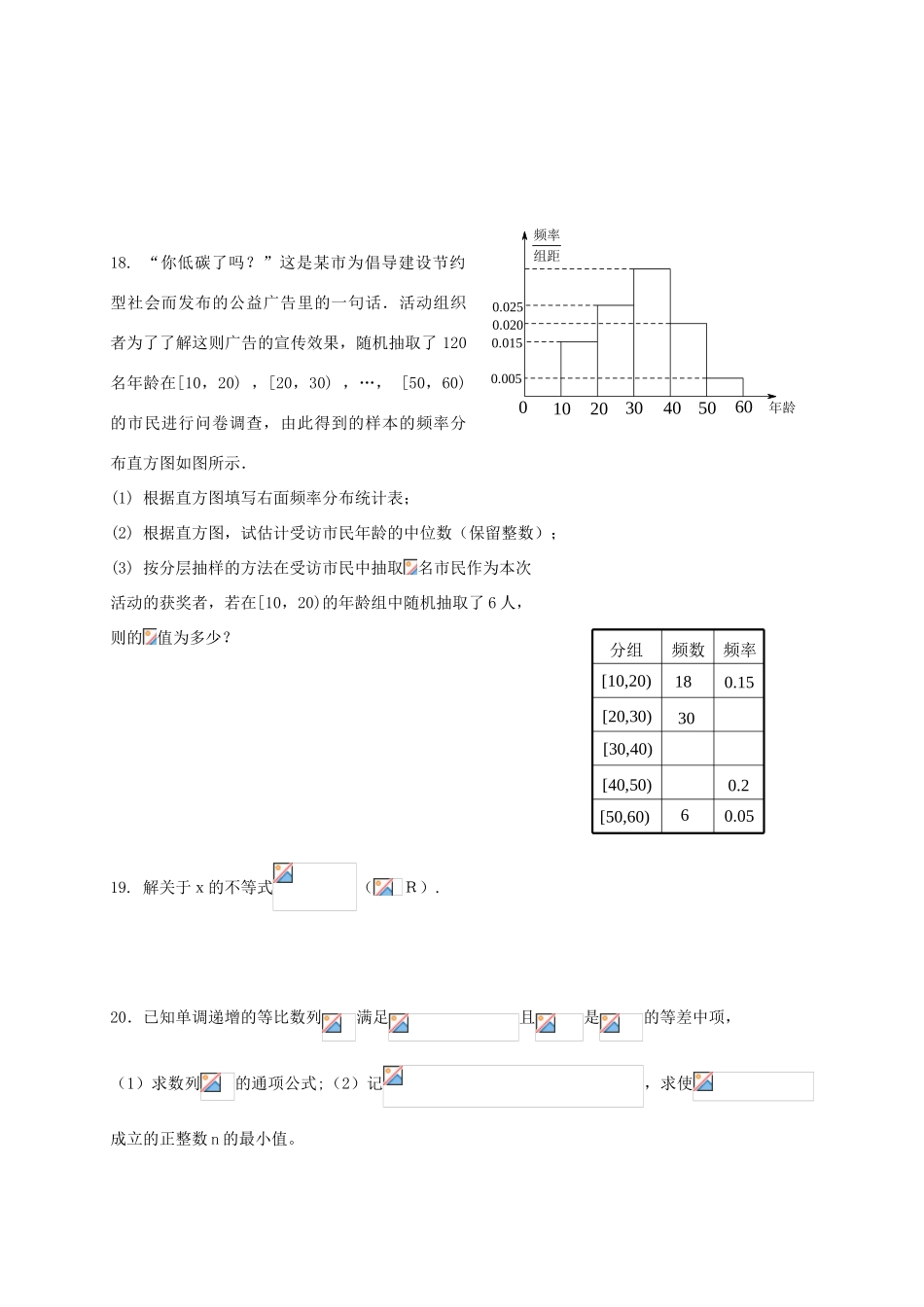
江西省南昌市2016-2017学年高一数学5月月考试题一、选择题1、不等式的解集为()A.B.C.D.2.已知{an}是递增数列,且对任意n∈N*都有an=n2+λn恒成立,则实数λ的取值范围是()A.(-,+∞)B.(0,+∞)C.[-2,+∞)D.(-3,+∞)3.在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是()A.钝角三角形B.直角三角形C.锐角三角形D.不能确定4.10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12.设其平均数为a,中位数为b,众数为c,则有A.a>b>cB.b>c>aC.c>a>bD.c>b>a5、已知不等式解集为,则a+b=A.-5B.5C.-1D.1B6.在△ABC中,角A,B,C的对边分别为a,b,c,若a=,b=,B=45°,则A=()A.30°B.30°或105°C.60°D.60°或120°7、C8.设有一个直线回归方程为,则变量增加一个单位时A.平均增加1.5个单位B.平均增加2个单位C.平均减少1.5个单位D.平均减少2个单位9.若x>0,y>0且,则xy有()A.最大值64B.最小值C.最小值D.最小值6410.某人从湖里打了一网鱼,共m条,做上记号再放入湖中,数日后又打了一网共n条,其中做记号的k条,估计湖中有鱼()条A、B、C、D、不确定11.在△ABC中,已知tan=sinC,给出以下四个结论:①=1;②1b>c,且+≥恒成立,则m的取值范围是________.14.一个总体的60个个体的编号为0,1,2,…,59,现要从中抽取一个容量为10的样本,请根据编号按被6除余3的方法,取足样本,则抽取的样本号码是.15.已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:22223242526272829210……记M(s,t)表示该数阵中第s行的第t个数,则M(11,2)对应的数是________(用2n的形式表示,n∈N).16.下列命题中:①函数的最小值是:②在△ABC中,若,则△ABC是等腰或直角三角形;③如果正实数,a,b,c满足a+b>c,则;其中正确的命题是三、解答题17.在中,已知.(1)求的大小;(2)设角的对边依次为,若,且是锐角三角形,求的取值范围;18.“你低碳了吗?”这是某市为倡导建设节约型社会而发布的公益广告里的一句话.活动组织者为了了解这则广告的宣传效果,随机抽取了120名年龄在[10,20),[20,30),…,[50,60)的市民进行问卷调查,由此得到的样本的频率分布直方图如图所示.(1)根据直方图填写右面频率分布统计表;(2)根据直方图,试估计受访市民年龄的中位数(保留整数);(3)按分层抽样的方法在受访市民中抽取名市民作为本次活动的获奖者,若在[10,20)的年龄组中随机抽取了6人,则的值为多少?19.解关于x的不等式(R).20.已知单调递增的等比数列满足且是的等差中项,(1)求数列的通项公式;(2)记,求使成立的正整数n的最小值。0.050.20.1563018[40,50)[30,40)[50,60)[20,30)[10,20)频率频数分组0频率组距年龄0.0250.0200.0150.00560504030201021.某国际化妆品生产企业为了占有更多的市场份额,拟在2012年英国伦敦奥运会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2012年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完.(1)将2012年的利润y(万元)表示为促销费t(万元)的函数.(2)该企业2012年的促销费投入多少万元时,企业的年利润最大?(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)22.已知有穷数列共有2项(整数),首项。设该数列的前n项和为,且,其中常数。(1)求证:数列{an}是等比数列;(2)若,数列满足,求数列的通项公式。(3)若(2)中的数列满足不等式,求K的值高一数学答案一、选择题1、不等式的解集为()A.B.C.D.A2.已...