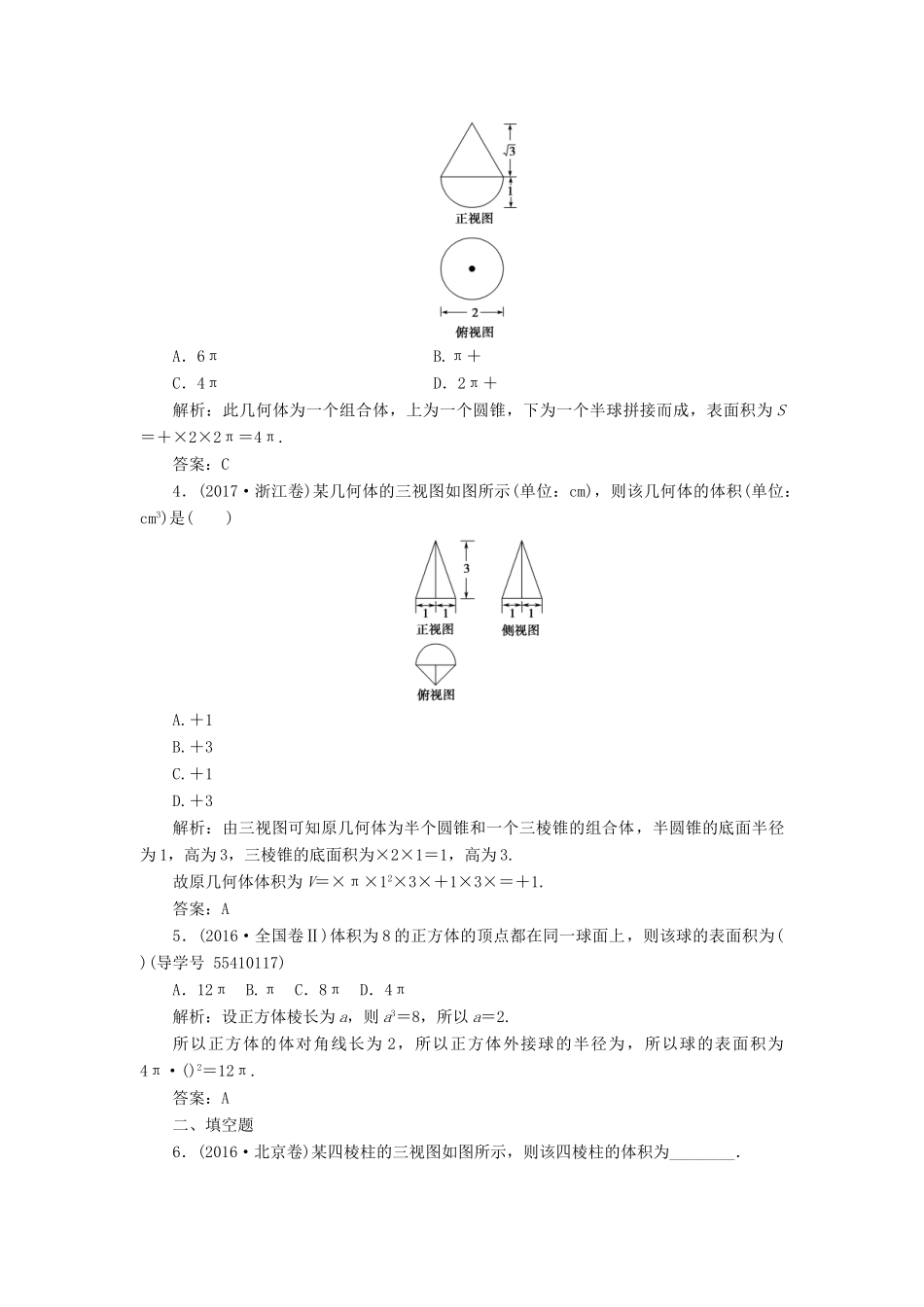
第1讲空间几何体的三视图、表面积及体积一、选择题1.如图所示是一个物体的三视图,则此三视图所描述物体的直观图是()解析:先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确.答案:D2.某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x的值是()A.2B.C.D.3解析:由三视图知,该几何体是四棱锥,底面是直角梯形,且S底=(1+2)×2=3.所以V=x·3=3,解得x=3.答案:D3.(2017·衡阳第二次联考)如下图所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为()A.6πB.π+C.4πD.2π+解析:此几何体为一个组合体,上为一个圆锥,下为一个半球拼接而成,表面积为S=+×2×2π=4π.答案:C4.(2017·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.+1B.+3C.+1D.+3解析:由三视图可知原几何体为半个圆锥和一个三棱锥的组合体,半圆锥的底面半径为1,高为3,三棱锥的底面积为×2×1=1,高为3.故原几何体体积为V=×π×12×3×+1×3×=+1.答案:A5.(2016·全国卷Ⅱ)体积为8的正方体的顶点都在同一球面上,则该球的表面积为()(导学号55410117)A.12πB.πC.8πD.4π解析:设正方体棱长为a,则a3=8,所以a=2.所以正方体的体对角线长为2,所以正方体外接球的半径为,所以球的表面积为4π·()2=12π.答案:A二、填空题6.(2016·北京卷)某四棱柱的三视图如图所示,则该四棱柱的体积为________.解析:由题意知该四棱柱为直四棱柱,其高为1,其底面为上底长为1,下底长为2,高为1的等腰梯形,所以该四棱柱的体积为V=×1=.答案:7.球面上有不同的三点A、B、C,且AB=BC=AC=3,球心到A,B,C所在截面的距离为球半径的一半,则球的表面积为________.解析:设球的球心为O,△ABC的中心为O′,在等边△ABC中,边长AB=3,则O′A=××3=.依题意,R2=+O′A2,得R=2.所以S球=4πR2=16π.答案:16π8.(2017·江苏卷)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是________.解析:设球半径为R,则圆柱底面圆半径为R,母线长为2R.又V1=πR2·2R=2πR3,V2=πR3,所以==.答案:三、解答题9.(2015·全国卷Ⅱ)如图,长方体ABCDA1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求平面α把该长方体分成的两部分体积的比值.解:(1)交线围成的正方形EHGF如图所示.(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为四边形EHGF为正方形,所以EH=EF=BC=10.于是MH==6,故AH=10,HB=6.故S四边形A1EHA=×(4+10)×8=56,S四边形EB1BH=×(12+6)×8=72.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.10.(2017·沈阳质检)在三棱柱ABCA1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.(导学号55410118)(1)证明:A1O⊥平面ABC;(2)求三棱锥C1ABC的体积.(1)证明:因为AA1=A1C,且O为AC的中点,所以A1O⊥AC,又平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,且A1O⊂平面AA1C1C,所以A1O⊥平面ABC.(2)解:因为A1C1∥AC,A1C1⊄平面ABC,AC⊂平面ABC,所以A1C1∥平面ABC,即C1到平面ABC的距离等于A1到平面ABC的距离.由(1)知A1O⊥平面ABC且A1O==,所以VC1ABC=VA1ABC=S△ABC·A1O=××2××=1.11.(2017·贵阳调研)如图,四边形ABCD为菱形,G是AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥EACD的体积为,求该三棱锥的侧面积.(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.因为BE⊥平面ABCD,AC⊂平面ABCD,所以AC⊥BE.因为BE∩BD=B,故AC⊥平面BED.又AC⊂平面AEC,所以平面AEC⊥平面BED.(2)解:设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.因为AE⊥EC,所以在Rt△AEC中,可得EG=x.由BE⊥平面ABCD,BG⊂平面ABCD知BE⊥BG,故△EBG为直角三角形,可得BE=x.由已知得,三棱锥EACD的体积VEACD=×AC·GD·BE=x3=.故x=2.从而可得AE=EC=ED=.所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.故三棱锥EACD的侧面积为3+2.