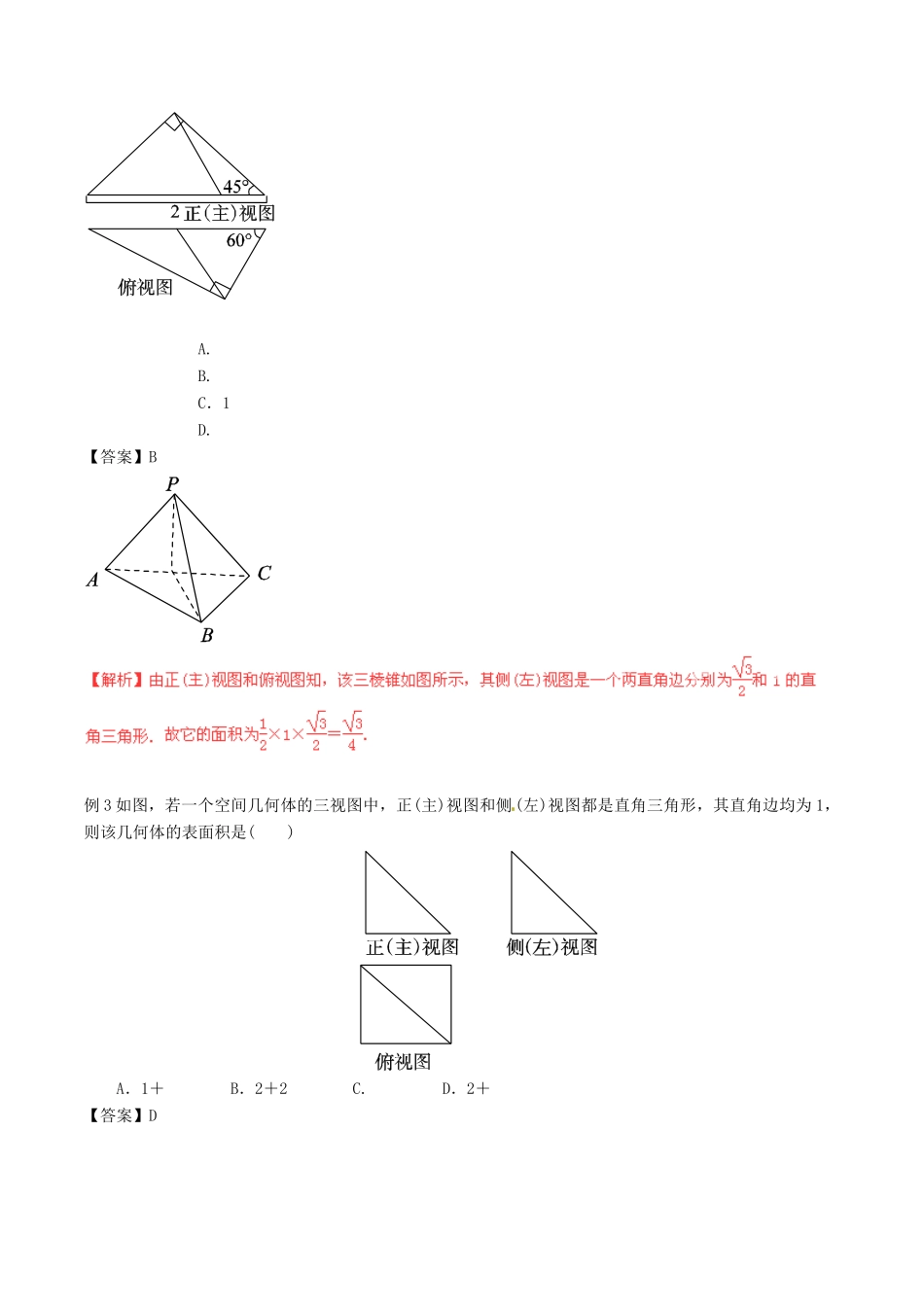
专题12立体几何三视图【背一背基础知识】1.投影:区分中心投影与平行投影。平行投影分为正投影和斜投影。2.三视图——是观察者从三个不同位置观察同一个空间几何体而画出的图形;正视图——光线从几何体的前面向后面正投影,得到的投影图;侧视图——光线从几何体的左面向右面正投影,得到的投影图;正视图——光线从几何体的上面向下面正投影,得到的投影图;注:(1)俯视图画在正视图的下方,“长度”与正视图相等;侧视图画在正视图的右边,“高度”与正视图相等,“宽度”与俯视图。(简记为“正、侧一样高,正、俯一样长,俯、侧一样宽”.(2)正视图,侧视图,俯视图都是平面图形,而不是直观图。3.直观图——是观察着站在某一点观察一个空间几何体而画出的图形。直观图通常是在平行投影下画出的空间图形。【讲一讲基本技能】1.必备技能:三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求:正俯一样长,俯侧一样宽,正侧一样高.一般地,若俯视图中出现圆,则该几何体可能是球或旋转体,若俯视图是多边形,则该几何体一般是多面体;若主视图和左视图中出现三角形,则该几何体可能为椎体。2.典型例题例1已知三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧(左)视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为()【答案】C例2已知一个三棱锥的正(主)视图与俯视图如图所示,则该三棱锥的侧(左)视图的面积为()A.B.C.1D.【答案】B例3如图,若一个空间几何体的三视图中,正(主)视图和侧(左)视图都是直角三角形,其直角边均为1,则该几何体的表面积是()A.1+B.2+2C.D.2+【答案】D【练一练趁热打铁】1.如图1是一个几何体的三视图.若它的体积是3,则a=________.【答案】2.一个几何体的正(主)视图和俯视图如图2所示,其中俯视图是边长为2的正三角形,且圆与三角形内切,则侧(主)视图的面积为()A.6+πB.4+πC.6+4πD.4+4π【答案】A3.如图,三棱柱的棱长为2,底面是边长为2的正三角形,,正视图是边长为2的正方形,俯视图为正三角形,则左视图的面积为()A.4B.C.D.2【答案】C几何体的表面积和体积【背一背基础知识】1..柱体、锥体、台体和球的表面积与体积(1)表面积公式(2)体积公式①圆柱的表面积S=2πr(r+l);①柱体的体积V=Sh;②圆锥的表面积S=πr(r+l);②锥体的体积V=Sh;③圆台的表面积S=π(r′2+r2+r′l+rl);③台体的体积V=(S′++S)h;④球的表面积S=4πR2④球的体积V=πR【讲一讲基本技能】1.必备技能:求几何体的表面积及体积问题,可以多角度、多方位地考虑,熟记公式是关键所在。求三棱锥的体积,等积转化法是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上。2.求不规则几何体的体积,常用分割或补形的思想,将不规则几何体转化为规则几何体以易于求解。3.典型例题例1.一个几何体的三视图如图3所示,则该几何体的体积为________.【答案】【分析】由三视图可以知道该几何体是圆柱与长方体的组合体,要分别求出体积加和.例2一个几何体的三视图如图所示,则该几何体的外接球的体积为()A.4πB.12πC.2πD.4π【答案】A【练一练趁热打铁】1.若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为.【答案】【解析】设圆柱的底面半径为r,高为h,底面积为s.体积为V,则有,所以底面面积,所以.2.三棱锥的侧棱两两垂直且长度分别为2cm,2cm,1cm,则其外接球的表面积是cm2.【答案】异面直线所成角【背一背基础知识】1.异面直线的定义:不同在任何一个平面的两条直线叫做异面直线2.异面直线所成的角的范围:.3.异面直线的判定方法:4异面直线所求的角的求法:①平移法→构造三角形→解三角形→余弦定理⑵平移→【讲一讲基本技能】1.必备技能:异面直线的平移方法常见的有三种平移方法:直接平移,中位线平移(尤其是图中出现了中点)补形平移“补形法”是立体几何中一种常见的方法,通过补形,可将问题转化为易于研究的几何体来处理,利用“补形法”找两异面直线所成的角也是常用的方法之一。2.典型例题例1.如图,...