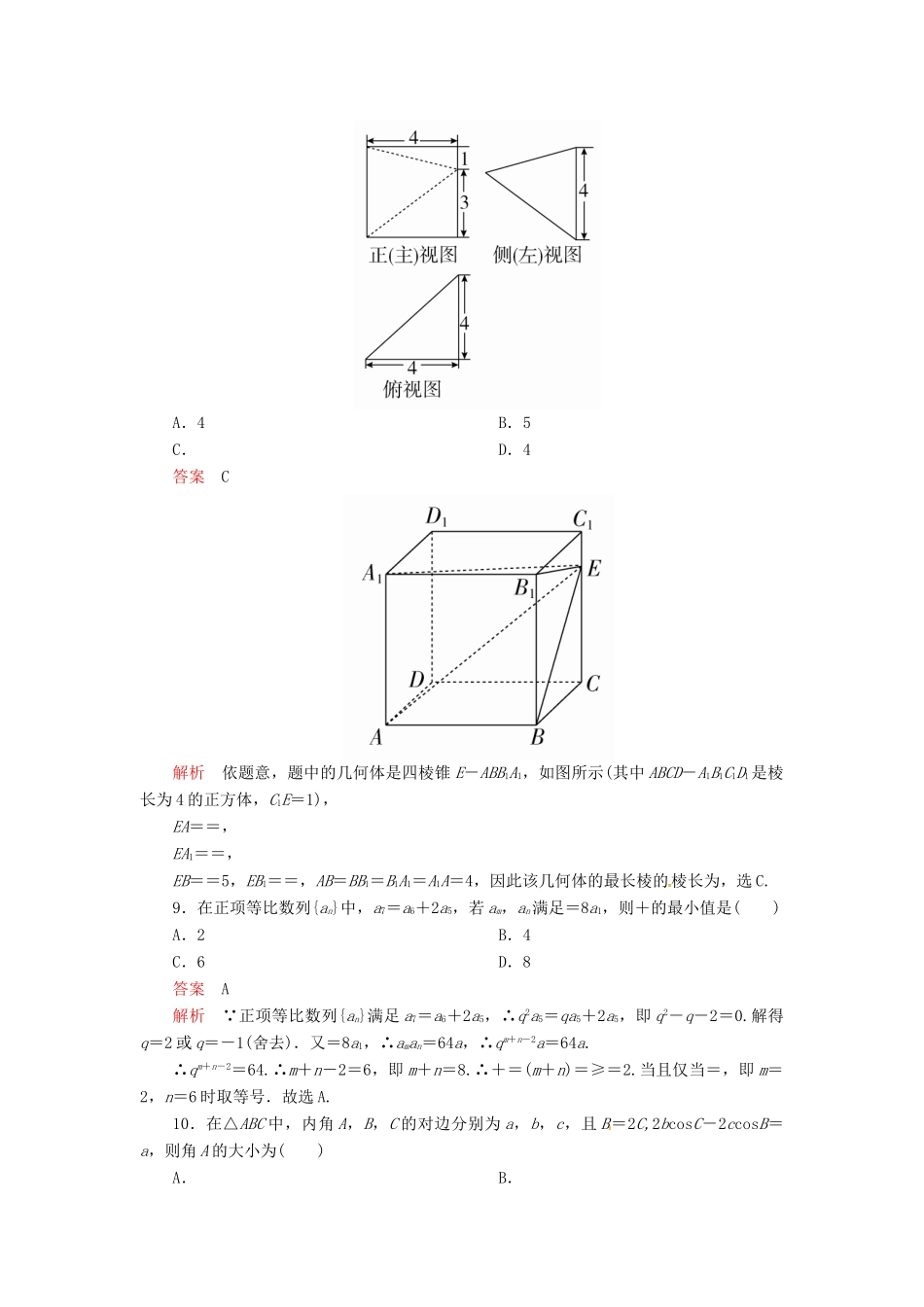
三基保分强化训练(八)1.设集合P={x|x<-3},Q={x|x2>4},则下列结论正确的是()A.P=QB.P∪Q=RC.P⊆QD.P∩Q=∅答案C解析因为Q={x|x2>4}={x|x<-2或x>2},所以P⊆Q,故选C.2.已知i为虚数单位,复数z满足z=(2-z)i3,现有下列四个命题:p1:z=1-i;p2:复数z的共轭复数是1+i;p3:复数z在复平面内对应的点位于第二象限;p4:|z|=.其中真命题的个数为()A.0B.2C.3D.4答案C解析因为z=(2-z)i3,所以z=zi-2i,所以(1-i)z=-2i,所以z===-i(1+i)=1-i,所以p1为真命题;根据共轭复数的定义知,复数z的共轭复数是1+i,所以p2为真命题;复数z在复平面内对应的点的坐标为(1,-1),位于第四象限,所以p3为假命题;|z|==,所以p4为真命题.综上,真命题的个数为3,故选C.3.设a=2017,b=log2017,c=log2018,则()A.c>b>aB.b>c>aC.a>c>bD.a>b>c答案D解析 a=2017>20170=1,0b>c.故选D.4.圆C1:x2+y2-4x+2y+1=0和圆C2:x2+y2+4y=-3的位置关系是()A.相离B.外切C.内切D.相交答案D解析将圆的一般方程转化为标准方程,圆C1:(x-2)2+(y+1)2=4,圆C2:x2+(y+2)2=9,则C1(2,-1),圆C1的半径r1为2;C2(0,-2),圆C2的半径r2为3.两圆的圆心距d==∈(r2-r1,r2+r1),所以两圆的位置关系是相交.故选D.5.对于直线m,n和平面α,β,m⊥α成立的一个充分条件是()A.m⊥n,n∥αB.m∥β,β⊥αC.m⊥β,n⊥β,n⊥αD.m⊥n,n⊥β,β⊥α答案C解析对于选项C,因为m⊥β,n⊥β,所以m∥n,又n⊥α,所以m⊥α,故选C.6.已知函数f(x)=2sin(2x+φ)(0<φ<π),若将函数f(x)的图象向右平移个单位长度后,所得图象关于y轴对称,则下列结论中不正确的是()A.φ=B.是f(x)图象的一个对称中心C.f(φ)=-2D.x=-是f(x)图象的一条对称轴答案C解析由题意得,变换后的函数g(x)=f=2sin的图象关于y轴对称,则-+φ=+kπ,k∈Z,因为0<φ<π,所以φ=,故A正确;f(x)=2sin,由2x+=kπ,k∈Z,得对称中心的横坐标为-+,k∈Z,故是f(x)图象的一个对称中心,故B正确;f(φ)=2sin=2sin=2,故C不正确;由2x+=+kπ,k∈Z,得x=-+,k∈Z,则x=-是f(x)图象的一条对称轴,故D正确.7.已知双曲线-=1(a>0,b>0)的渐近线与圆(x-4)2+y2=4相切,则该双曲线的离心率为()A.2B.C.D.答案B解析不妨取双曲线的一条渐近线ON的方程为y=x,N为切点,如图所示,设圆(x-4)2+y2=4的圆心为M,连接MN,则MN⊥ON,|MN|=2,|OM|=4,∴∠NOM=30°,∴tan30°==,又a2+b2=c2,∴e==,故选B.8.一锥体的三视图如图所示,则该棱锥的最长棱的棱长为()A.4B.5C.D.4答案C解析依题意,题中的几何体是四棱锥E-ABB1A1,如图所示(其中ABCD-A1B1C1D1是棱长为4的正方体,C1E=1),EA==,EA1==,EB==5,EB1==,AB=BB1=B1A1=A1A=4,因此该几何体的最长棱的棱长为,选C.9.在正项等比数列{an}中,a7=a6+2a5,若am,an满足=8a1,则+的最小值是()A.2B.4C.6D.8答案A解析 正项等比数列{an}满足a7=a6+2a5,∴q2a5=qa5+2a5,即q2-q-2=0.解得q=2或q=-1(舍去).又=8a1,∴aman=64a,∴qm+n-2a=64a.∴qm+n-2=64.∴m+n-2=6,即m+n=8.∴+=(m+n)=≥=2.当且仅当=,即m=2,n=6时取等号.故选A.10.在△ABC中,内角A,B,C的对边分别为a,b,c,且B=2C,2bcosC-2ccosB=a,则角A的大小为()A.B.C.D.答案A解析由正弦定理得2sinBcosC-2sinCcosB=sinA=sin(B+C)=sinBcosC+cosBsinC,sinBcosC=3sinCcosB,sin2CcosC=3sinCcos2C,2cos2C=3(cos2C-sin2C),tan2C=,tanC=, B=2C,∴C为锐角,∴C=,B=,A=,故选A.11.关于x的方程xlnx-kx+1=0在区间上有两个不等实根,则实数k的取值范围是()A.B.(1,e-1]C.D.(1,+∞)答案A解析 xlnx-kx+1=0,∴k=lnx+.设f(x)=lnx+,则f′(x)=-=.令f′(x)=0,解得x=1.当x∈时,f′(x)<0,函数f(x)单调递减;当x∈[1,e]时,f′(x)>0,函数f(x)单调递增.故f(x)mi...