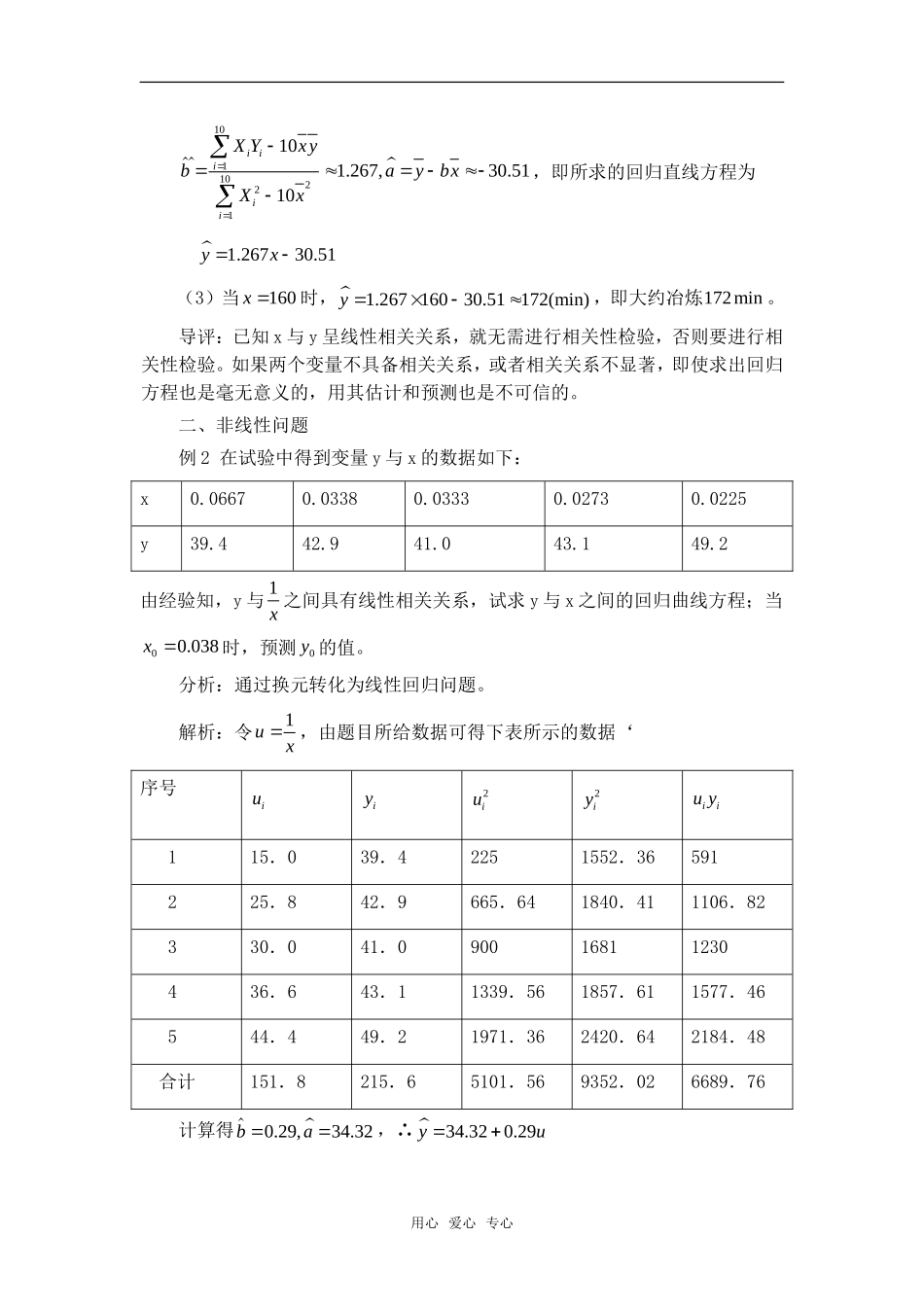
回归分析注意问题两例一、相关性判断问题例1炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料融化完毕时钢水的含碳量x与冶炼时间y(从炉料融化完毕到出钢的时间)的一列数据,如下表所示:x(0.01%)104180190177147134150191204121Y/min100200210185155135170205235125(1)y与x是否具有线性相关关系?(2)如果y与x具有线性相关关系,求回归直线方程;(3)预测当钢水含碳量为160个0.01%时,应冶炼多少分钟?分析:判断两变量之间是否具有线性相关关系,要计算出相关系数r,比较r与临界值的大小,依据线性回归直线方程,对冶炼时间进行预报。解析:(1)由已知数据列成下表:i12345678910ix104180190177147134150191204121iy100200210185155135170205235125iixy10400360003990032745227851809025500391554794015125159.8,172XY101022111265448,321350,287640niiiiiiiXyXY于是1011010102222111100.9906(10)(10)iiiiiiiiiXYxyrXxyy,又0.050.632r,0.05rr知y与x具有线性相关关系。(2)设所求的回归直线方程ybxa,则用心爱心专心10110221101.267,30.5110iiiiiXYxybaybxXx,即所求的回归直线方程为1.26730.51yx(3)当160x时,1.26716030.51172(min)y,即大约冶炼172min。导评:已知x与y呈线性相关关系,就无需进行相关性检验,否则要进行相关性检验。如果两个变量不具备相关关系,或者相关关系不显著,即使求出回归方程也是毫无意义的,用其估计和预测也是不可信的。二、非线性问题例2在试验中得到变量y与x的数据如下:x0.06670.03380.03330.02730.0225y39.442.941.043.149.2由经验知,y与1x之间具有线性相关关系,试求y与x之间的回归曲线方程;当00.038x时,预测0y的值。分析:通过换元转化为线性回归问题。解析:令1ux,由题目所给数据可得下表所示的数据‘序号iuiy2iu2iyiiuy115.039.42251552.36591225.842.9665.641840.411106.82330.041.090016811230436.643.11339.561857.611577.46544.449.21971.362420.642184.48合计151.8215.65101.569352.026689.76计算得0.29,34.32ba,∴34.320.29yu用心爱心专心故所求回归曲线方程为0.2934.32yx,当00.038x时,0.2934.3241.950.038y。导评:非线性问题有时并不给出经验公式,此时我们可以由已知的数据画出散点图,并把散点图与已经学习过的各种函数,如幂函数、指数函数、对数函数、二次函数等作比较,挑选出跟这些散点拟合最好的函数,然后再采用变量的置换把问题转化为线性回归分析问题,使问题得以解决。用心爱心专心