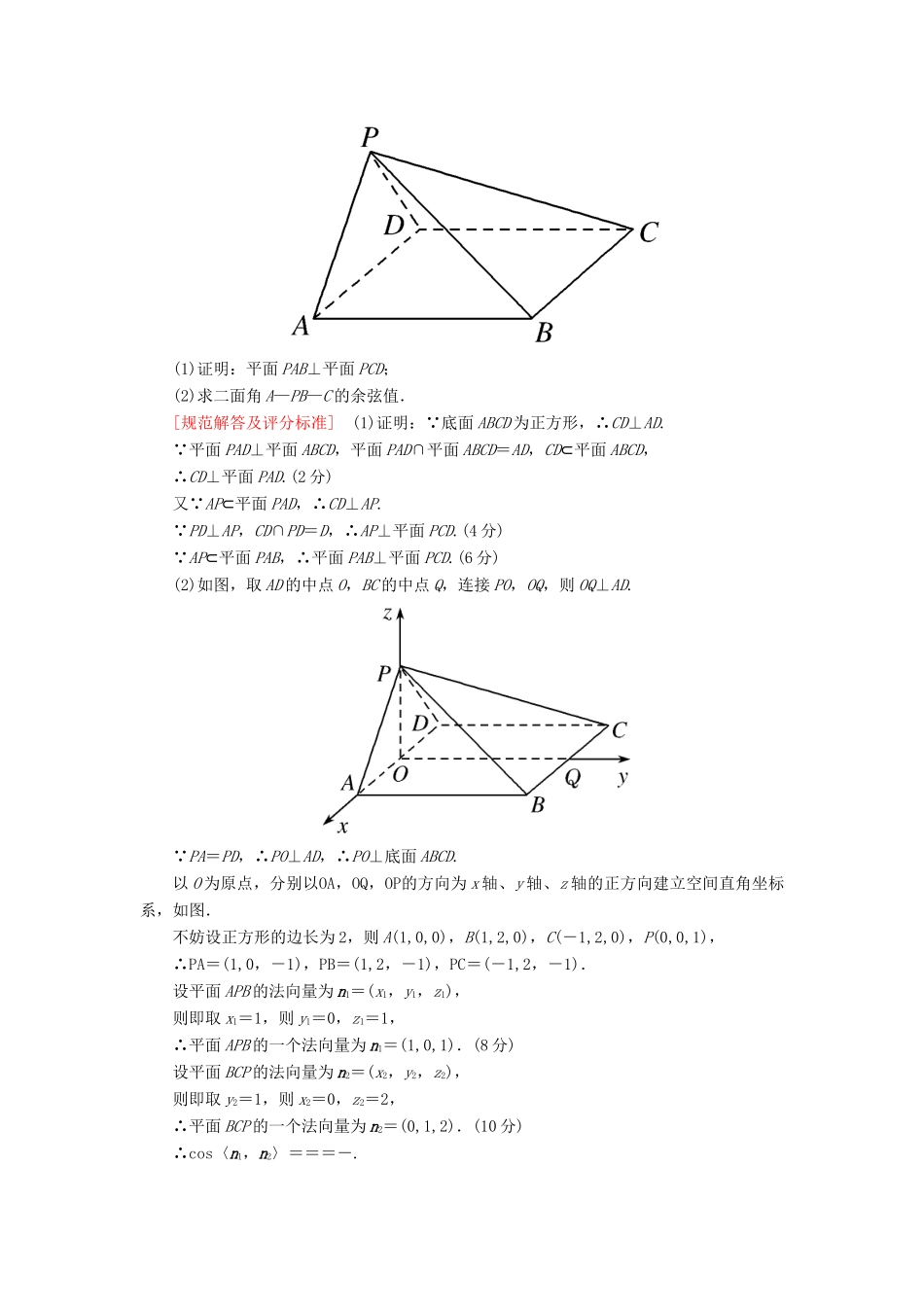
规范练(一)(时间:45分钟满分:46分)(2)将函数f(x)的图象向右平移个单位长度.得到函数g(x)=sin=-cos2x的图象,即g(x)=-cos2x,(8分)当x∈时,2x∈,可得cos2x∈,(10分)所以-cos2x∈,即函数g(x)在区间上的值域是.(12分)2.(12分)如图所示,在四棱锥P—ABCD中,平面PAD⊥平面ABCD,底面ABCD是正方形,且PA=PD,∠APD=90°.(1)证明:平面PAB⊥平面PCD;(2)求二面角A—PB—C的余弦值.[规范解答及评分标准](1)证明: 底面ABCD为正方形,∴CD⊥AD. 平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,∴CD⊥平面PAD.(2分)又 AP⊂平面PAD,∴CD⊥AP. PD⊥AP,CD∩PD=D,∴AP⊥平面PCD.(4分) AP⊂平面PAB,∴平面PAB⊥平面PCD.(6分)(2)如图,取AD的中点O,BC的中点Q,连接PO,OQ,则OQ⊥AD. PA=PD,∴PO⊥AD,∴PO⊥底面ABCD.以O为原点,分别以OA,OQ,OP的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,如图.不妨设正方形的边长为2,则A(1,0,0),B(1,2,0),C(-1,2,0),P(0,0,1),∴PA=(1,0,-1),PB=(1,2,-1),PC=(-1,2,-1).设平面APB的法向量为n1=(x1,y1,z1),则即取x1=1,则y1=0,z1=1,∴平面APB的一个法向量为n1=(1,0,1).(8分)设平面BCP的法向量为n2=(x2,y2,z2),则即取y2=1,则x2=0,z2=2,∴平面BCP的一个法向量为n2=(0,1,2).(10分)∴cos〈n1,n2〉===-.由图知所求二面角的平面角为钝角,故二面角A—PB—C的余弦值为-.(12分)3.(12分)有一个类似计步数据库的公众账号,用户只需以运动手环或手机协处理器的运动数据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现.现随机选取某人朋友圈中的50人记录了他们某一天的走路步数,并将数据整理如下表:规定:人一天行走的步数超过8000时被系统评定为“积极性”,否则被评定为“懈怠性”.(1)以这50人一天行走的步数的频率代替1人一天行走的步数发生的概率,记X表示随机抽取3人中被系统评定为“积极性”的人数,求P(X≤2)和X的数学期望;(2)为了调查评定系统的合理性,拟从这50人中先抽取10人(男性6人,女性4人).其中男性中被系统评定为“积极性\”的有4人,“懈怠性\”的有2人,从中任意选取3人,记选到“积极性\”的人数为x;其中女性中被系统评定为“积极性”和“懈怠性”的均有2人,从中任意选取2人,记选到“积极性”的人数为y.求x>y的概率.[规范解答及评分标准](1)被系统评定为“积极性”的概率为=,X~B.故P(X≤2)=1-3=,(4分)X的数学期望E(X)=3×=.(6分)(2)“x>y”包含“x=3,y=2”,“x=3,y=1”,“x=3,y=0”,“x=2,y=1”,“x=2,y=0”,“x=1,y=0”.P(x=3,y=2)=×=,P(x=3,y=1)=×=,P(x=3,y=0)=×=,P(x=2,y=1)=×=,P(x=2,y=0)=×=,P(x=1,y=0)=×=.所以P(x>y)=+++++=.(12分)选考题:共10分.请考生在第4、5题中任选一题作答.如果多做,那么按所做的第一题计分.4.[选修4-4:坐标系与参数方程](10分)在直角坐标系xOy中,倾斜角为α的直线l的参数方程为(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-2cosθ=0.(1)写出直线l的普通方程和曲线C的直角坐标方程;(2)已知点P(0,1),点Q(,0),直线l过点Q与曲线C相交于A,B两点,设线段AB的中点为M,求|PM|的值.[规范解答及评分标准](1)由直线l的参数方程消去t,得l的普通方程为xsinα-ycosα+cosα=0.(3分)由ρsin2θ-2cosθ=0,得ρ2sin2θ-2ρcosθ=0,则曲线C的直角坐标方程为y2=2x.(5分)(2)易得点P(0,1)在直线l上,所以tanα=kPQ==-,解得α=.所以l的参数方程为(7分)代入y2=2x中,得t2+16t+4=0.(8分)设A,B,M所对应的参数分别为t1,t2,t0,则t0==-8,所以|PM|=|t0|=8.(10分)5.[选修4-5:不等式选讲](10分)已知函数f(x)=|x-2|+|x+3|.(1)解不等式f(x)>6;(2)若关于x的不等式ax-1≤f(x)恒成立,求实数a的取值范围.[规范解答及评分标准](1)因为f(x)=(1分)所以当x<-3时,由f(x)>6,得-2x-1>6,解得x<-;(2分)当...