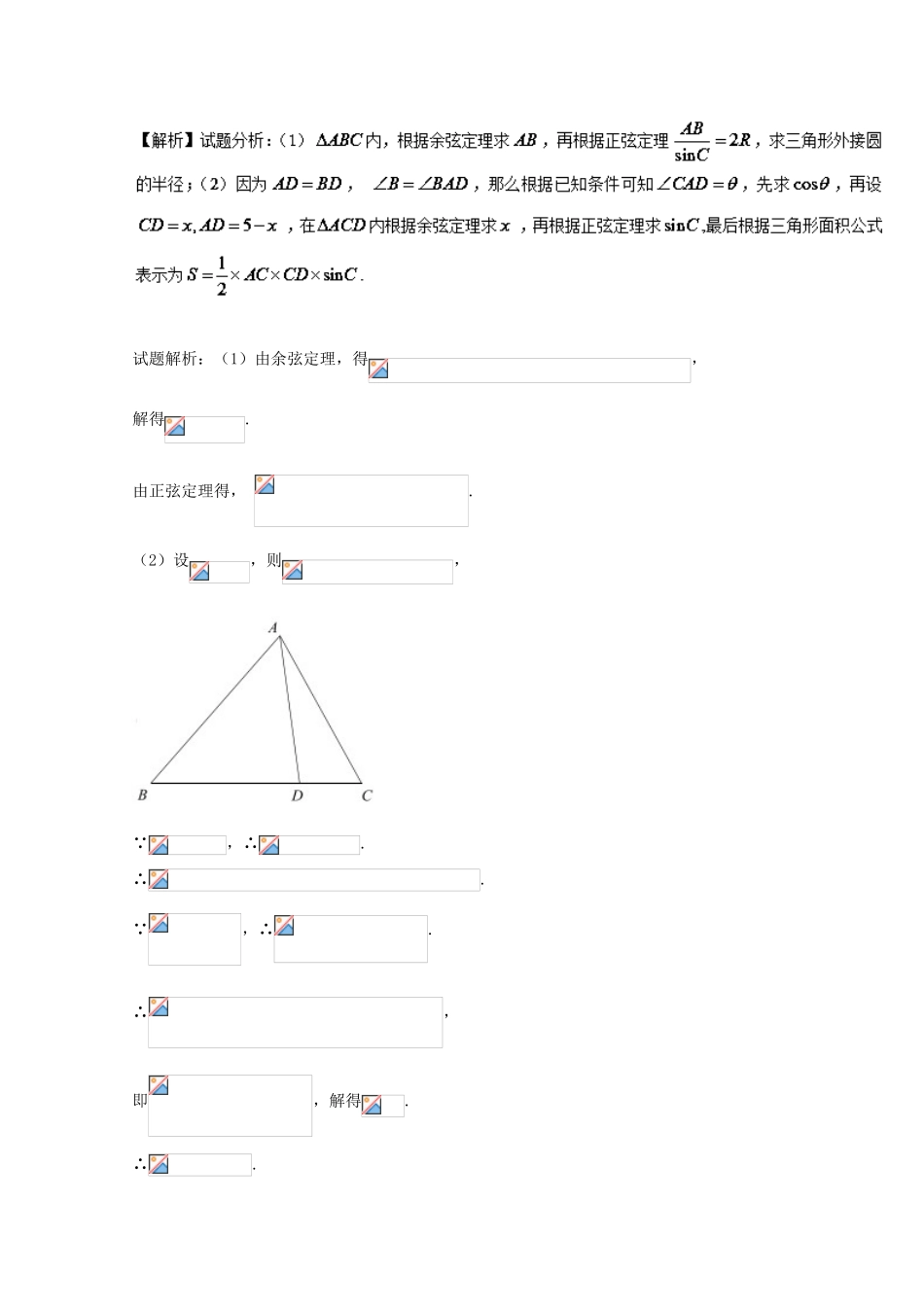
命题角度2.2:利用正弦、余弦定理解与三角形面积有关的问题1.已知的三个内角的对边分别为.(Ⅰ)若,求证:;(Ⅱ)若,且的面积,求角.【答案】(Ⅰ)详见解析(Ⅱ)【解析】试题分析:(Ⅰ)有条件及三角形内角和关系可得,再根据诱导公式可得,然后利用两角和余弦公式展开,结合二倍角公式及平方关系,将式子转化为关于的关系式,(Ⅱ)由三角形面积公式及余弦定理,代入条件化简得;再根据正弦定理将条件化角:,最后根据三角形内角关系消去C角得:,根据二倍角及配角公式可得,结合B角范围可得结果.(Ⅱ)在中,由余弦定理知:2.在中,为边上一点,,,.(1)若,求外接圆半径的值;(2)设,若,求的面积.【答案】(1);(2).试题解析:(1)由余弦定理,得,解得.由正弦定理得,.(2)设,则, ,∴.∴. ,∴.∴,即,解得.∴. ,∴.∴.3.如图,在中,角的对边分别为,.(1)求角的大小;(2)若为外一点,,求四边形面积的最大值.【答案】(1)(2)【解析】试题分析:(1)先根据正弦定理将条件转化为角的关系再利用三角形内角关系、诱导公式及两角和正弦公式化简得即得,.(2),由余弦定理得,将数据代入可得,利用配角公式得,最后根据三角形有界性可得四边形的面积最大值。4.在中,三边所对应的角分别是,已知成等比数列.(1)若,求角的值;(2)若外接圆的面积为,求面积的取值范围.【答案】(1);(2).【解析】试题分析:(1)先将切化弦变形得,利用等比数列性质和正弦定理得,进而得,即,由不是最大边得(2)易得外接圆半径,利用余弦定理和均值不等式得,即,再利用正弦定理和三角形正弦公式得,利用,进而解得.(2) 外接圆的面积为,∴的外接圆的半径,由余弦定理,得,又,∴.当且仅当时取等号,又 为的内角,∴,由正弦定理,得.∴的面积, ,∴,∴.考点:1、正弦定理;2、余弦定理;3、均值不等式.5.已知函数在区间上单调递增,在区间上单调递减.如图,四边形中,为的内角的对边,且满足.(1)证明:;(2)若,设,,,求四边形面积的最大值.【答案】(1)见解析;(2).试题解析:(1)由题意知:,解得:, ,∴,∴,∴.∴.(2)因为,,所以,所以为等边三角形,, ,∴,当且仅当,即时取最大值,的最大值为.6.已知中,角所对的边分别为,且,.(1)若,求的大小;(2)若为三个连续正整数,求的面积.【答案】(1)(2)的面积为【解析】试题分析:(1)由题意边化角,结合三角函数的性质可得,则.(2)由题意可设,,,,结合余弦定理得,据此可得的面积为.试题解析:(1) ,∴由正弦定理有,又,即,于是,在中,,于是,.(2)因为,故,故设,,,;由,得,∴.由余弦定理得:,代入可得:,解得:,∴,,,故,故,故的面积为.7.在中,分别是角的对边,成等比数列,且.(Ⅰ)求的大小;(Ⅱ)若,且,求的面积.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(Ⅰ)由是一个等比数列得:,得,再由余弦定理,即可求解角的值.(Ⅱ)由题意得或,分类讨论,利用正、余弦定理,即可求解的面积.试题解析:(Ⅰ)由是一个等比数列得:,所以由得,,,又(Ⅱ)由得:,①当,由题意,,,所以由正弦定理得:,,故由勾股定理得:,②当时,由题意,,,所以由余弦定理得:,,,,综上①②得:的面积:8.在中,已知分别是角的对边,且。(1)若,求的值;(2)若,求的面积的最大值。【答案】(1);(2)1.【解析】试题分析:(1)由题意结合正弦定理可得是等腰直角三角形,则;(2)结合余弦定理得到面积的表达式,然后利用均值不等式的结论可得的面积的最大值是1.法2:因为,所以由余弦定理,得即所以(2)因为,,所以由余弦定理,得所以因为,所以所以的面积由,所以时,的最大值为2故的面积所以的面积的最大值为19.四边形如图所示,已知,.(1)求的值;(2)记与的面积分别是与,求的最大值.【答案】(1);(2)14.【解析】试题分析:(1)在中,分别用余弦定理,列出等式,得出的值;(2)分别求出的表达式,利用(1)的结果,得到是关于的二次函数,利用三角形两边之和大于第三边,两边之差小于第三边,求出的范围,由的范围求出的范围,再求出的最大值.试题解...