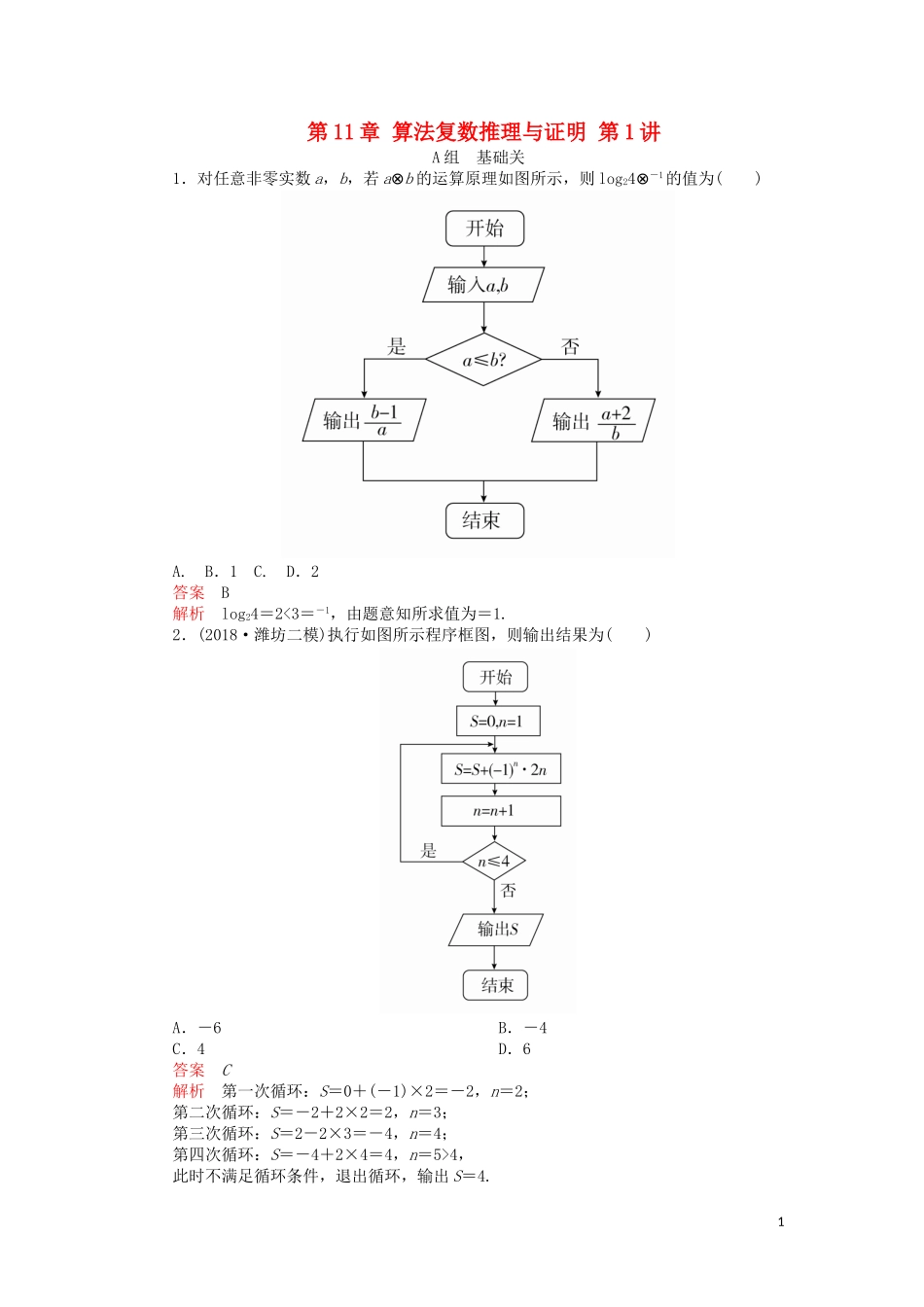
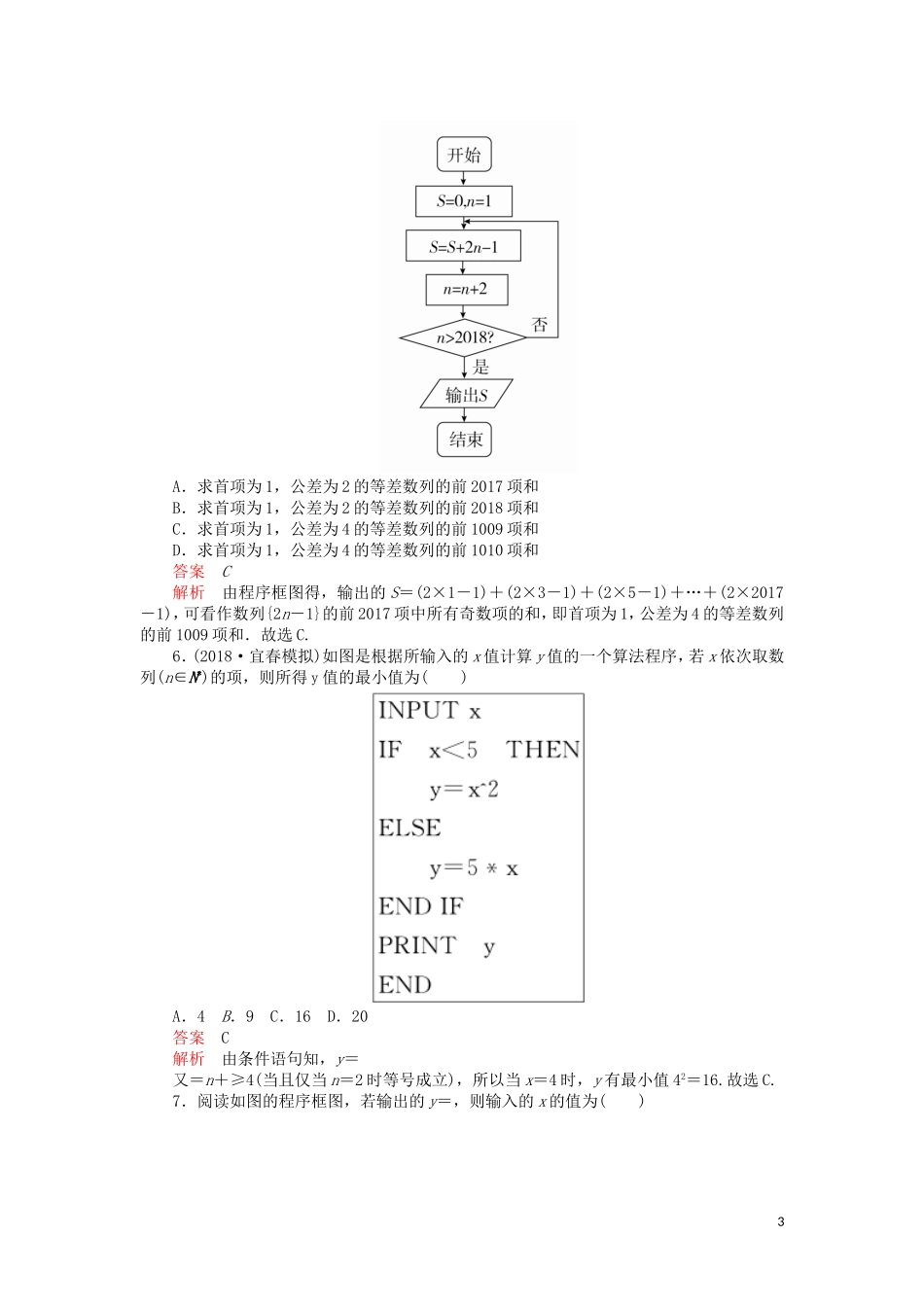
第11章算法复数推理与证明第1讲A组基础关1.对任意非零实数a,b,若a⊗b的运算原理如图所示,则log24⊗-1的值为()A.B.1C.D.2答案B解析log24=2<3=-1,由题意知所求值为=1.2.(2018·潍坊二模)执行如图所示程序框图,则输出结果为()A.-6B.-4C.4D.6答案C解析第一次循环:S=0+(-1)×2=-2,n=2;第二次循环:S=-2+2×2=2,n=3;第三次循环:S=2-2×3=-4,n=4;第四次循环:S=-4+2×4=4,n=5>4,此时不满足循环条件,退出循环,输出S=4.13.(2018·重庆调研)阅读如图所示的程序框图,为使输出S的数据为160,则判断框中应填入的条件为()A.k≤3?B.k≤4?C.k≤5?D.k≤6?答案C解析执行程序框图,S=0,k=1→S=2,k=2→S=8,k=3→S=24,k=4→S=64,k=5→S=160,k=6,不满足判断框内的条件,终止循环,结合选项知,判断框中应填入的条件为“k≤5?”,故选C.4.如图所示的程序框图是为了求出满足2n-n2>28的最小偶数n,那么在空白框内填入及最后输出的n值分别是()A.n=n+1和6B.n=n+2和6C.n=n+1和8D.n=n+2和8答案D解析由于要求出满足2n-n2>28的最小偶数,所以空白框内应填n=n+2,执行程序如下:n=0,A=20-02=1≤28;n=2,A=22-22=0≤28;n=4,A=24-42=0≤28;n=6,A=26-62=28≤28;n=8,A=28-82=192>28,输出n=8,所以选D.5.(2018·洛阳一模)已知某算法的程序框图如图所示,则该算法的功能是()2A.求首项为1,公差为2的等差数列的前2017项和B.求首项为1,公差为2的等差数列的前2018项和C.求首项为1,公差为4的等差数列的前1009项和D.求首项为1,公差为4的等差数列的前1010项和答案C解析由程序框图得,输出的S=(2×1-1)+(2×3-1)+(2×5-1)+…+(2×2017-1),可看作数列{2n-1}的前2017项中所有奇数项的和,即首项为1,公差为4的等差数列的前1009项和.故选C.6.(2018·宜春模拟)如图是根据所输入的x值计算y值的一个算法程序,若x依次取数列(n∈N*)的项,则所得y值的最小值为()A.4B.9C.16D.20答案C解析由条件语句知,y=又=n+≥4(当且仅当n=2时等号成立),所以当x=4时,y有最小值42=16.故选C.7.阅读如图的程序框图,若输出的y=,则输入的x的值为()3A.-1B.1C.1或5D.-1或1答案B解析这是一个用条件分支结构设计的算法,该程序框图所表示的算法的作用是求分段函数y=的函数值,输出的结果为,当x≤2时,sinx=,解得x=1+12k或x=5+12k,k∈Z,即x=1,-7,-11,…;当x>2时,2x=,解得x=-1(舍去),则输入的x可能为1,故选B.8.按照如图程序运行,则输出的K的值是________.答案3解析第一次循环,X=7,K=1;第二次循环,X=15,K=2;第三次循环,X=31,K=3,X>16,终止循环,则输出K的值是3.9.美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了4优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,每次运算都精确到小数点后两位,则输出的结果为________.答案2.84解析输入a=8,n=2,ξ=0.5,m==4,n==3,|4-3|=1>0.5;m=≈2.67,n≈=2.84,|2.67-2.84|=0.17<0.5,输出n=2.84.10.执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为________.答案25解析当条件x≥0,y≥0,x+y≤1不成立时,输出S的值为1,当条件x≥0,y≥0,x+y≤1成立时,输出S=2x+y,下面用线性规划的方法求此时S的最大值.作出不等式组表示的平面区域如图中阴影部分所示,由图可知当直线S=2x+y经过点M(1,0)时S最大,其最大值为2×1+0=2,故输出S的最大值为2.B组能力关1.(2018·广东肇庆一模)图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为A1,A2,…,A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是()A.7B.8C.9D.10答案D解析该程序的作用是求考试成绩不低于90分的次数,根据茎叶图可得不低于90分的次数为10.故选D.2.下图的程序框图的算法思路源于我国古代数学名著《数书九章》中...