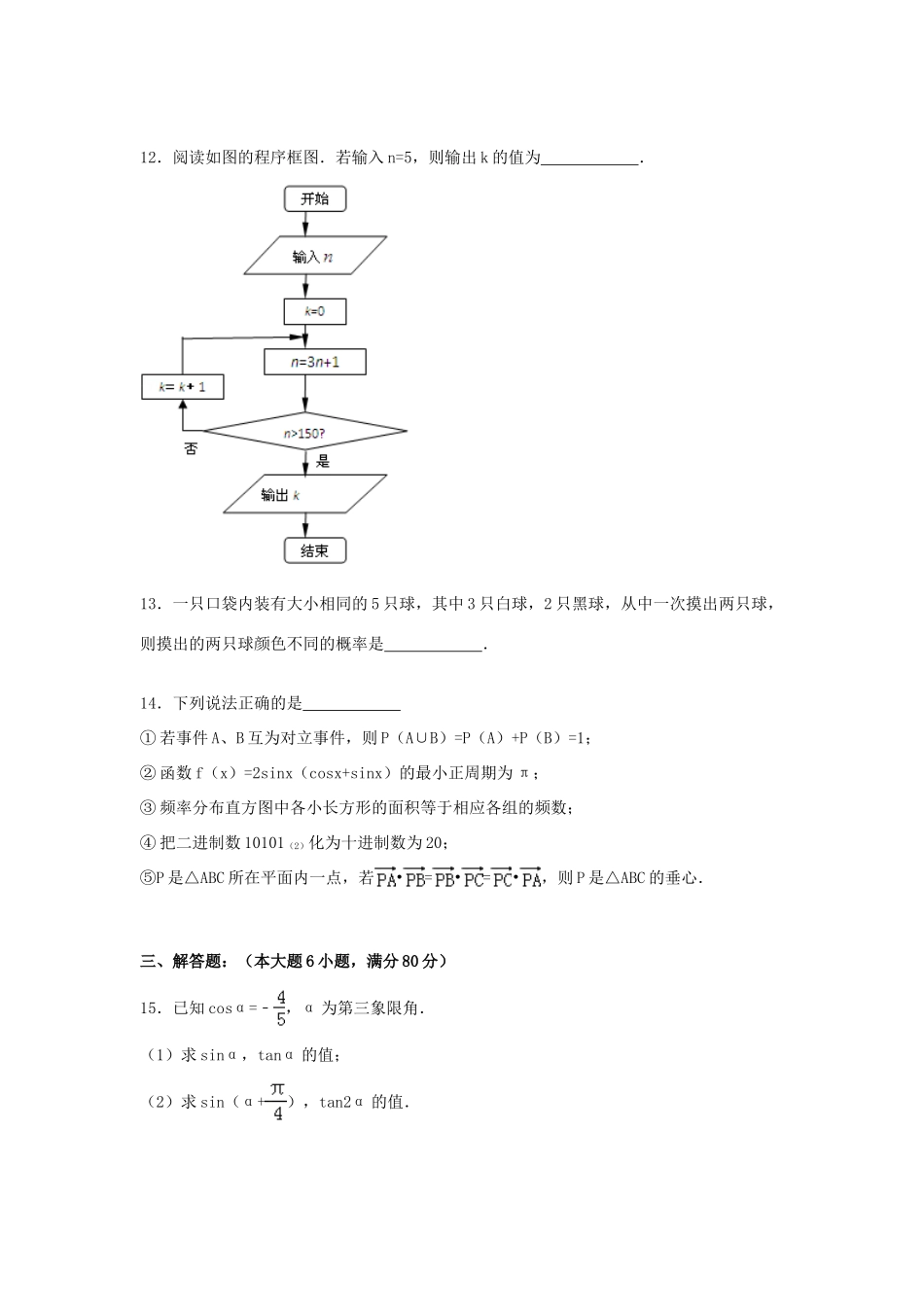
2014-2015学年广东省中山市高一(下)期末数学模拟试卷一、选择题:(本大题10小题,每小题5分,满分50分)1.sin(﹣225°)的值是()A.B.C.D.2.某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家.为了掌握各商店的营业情况,要从中抽取一个容量为20的样本.若采用分层抽样的方法,抽取的中型商店数是()A.2B.3C.5D.133.方程x2+y2+2x﹣4y﹣6=0表示的圆形是()A.以(1,﹣2)为圆心,为半径的圆B.以(1,2)为圆心,为半径的圆C.以(﹣1,﹣2)为圆心,为半径的圆D.以(﹣1,2)为圆心,为半径的圆4.下列各式中,值为的是()A.2sin15°cos15°B.cos215°﹣sin215°C.2sin215°﹣1D.sin215°+cos215°5.已知函数f(x)=sin(ωx+)(ω>0)的图象的两相邻对称轴之间的距离为,要得到y=f(x)的图象,只须把y=sinωx的图象()A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位6.某产品的广告费用x与销售额y的统计数据如下表:广告费用x万元)2345销售额y(万元)26394954根据上表可得回归方程中的b为9.4,据此模型推测广告费用为7万元时销售额为()A.74.2万元B.74.9万元C.75.3万元D.76.1万元7.函数f(x)=2sin(ωx+φ)(ω>0,﹣<φ<)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣B.2,﹣C.4,﹣D.4,8.在区间[﹣1,1]上任取两个数x、y,则满足的概率是()A.B.C.D.9.在△ABC中,点D在BC边上,且=3,=r+s,则的值是()A.1B.C.D.310.已知直线ax+by+c=0与圆O:x2+y2=1相交于A,B两点,且,则的值是()A.B.C.D.0二、填空题(本大题4小题,每小题5分,共20分)11.已知=(4,2),=(x,﹣3),且∥,则x的值为.12.阅读如图的程序框图.若输入n=5,则输出k的值为.13.一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出两只球,则摸出的两只球颜色不同的概率是.14.下列说法正确的是①若事件A、B互为对立事件,则P(A∪B)=P(A)+P(B)=1;②函数f(x)=2sinx(cosx+sinx)的最小正周期为π;③频率分布直方图中各小长方形的面积等于相应各组的频数;④把二进制数10101(2)化为十进制数为20;⑤P是△ABC所在平面内一点,若•=•=•,则P是△ABC的垂心.三、解答题:(本大题6小题,满分80分)15.已知cosα=﹣,α为第三象限角.(1)求sinα,tanα的值;(2)求sin(α+),tan2α的值.16.已知向量=3﹣2,=4+,其中=(1,0),=(0,1),求:(1)求•的值;(2)求与夹角θ的余弦值.(3)求在方向上的投影.17.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.(1)求x和y的值;(2)计算甲班7位学生成绩的方差s2;(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.参考公式:方差,其中.18.已知函数f(x)=2cosx(sinx﹣cosx)+1.(1)求函数f(x)的最小正周期及单调增区间;(2)画出函数y=f(x)在区间[0,π]内的图象;(3)说明f(x)的图象可由y=sinx的图象经过怎样的变换得到的,并求f(x)在x∈[,]的值域.19.一汽车厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):轿车A轿车B轿车C舒适型100150z标准型300450600按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.(1)求z的值;(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.20.已知半径为5的圆的圆心在x轴上,圆心的横坐标是整数,且与直线4x+3y﹣29=0相切.求:(Ⅰ)求圆的方程;(Ⅱ)设直线ax﹣y+5=0与圆相交于A,B两点,求实数a的取值范围;(Ⅲ)在(2...