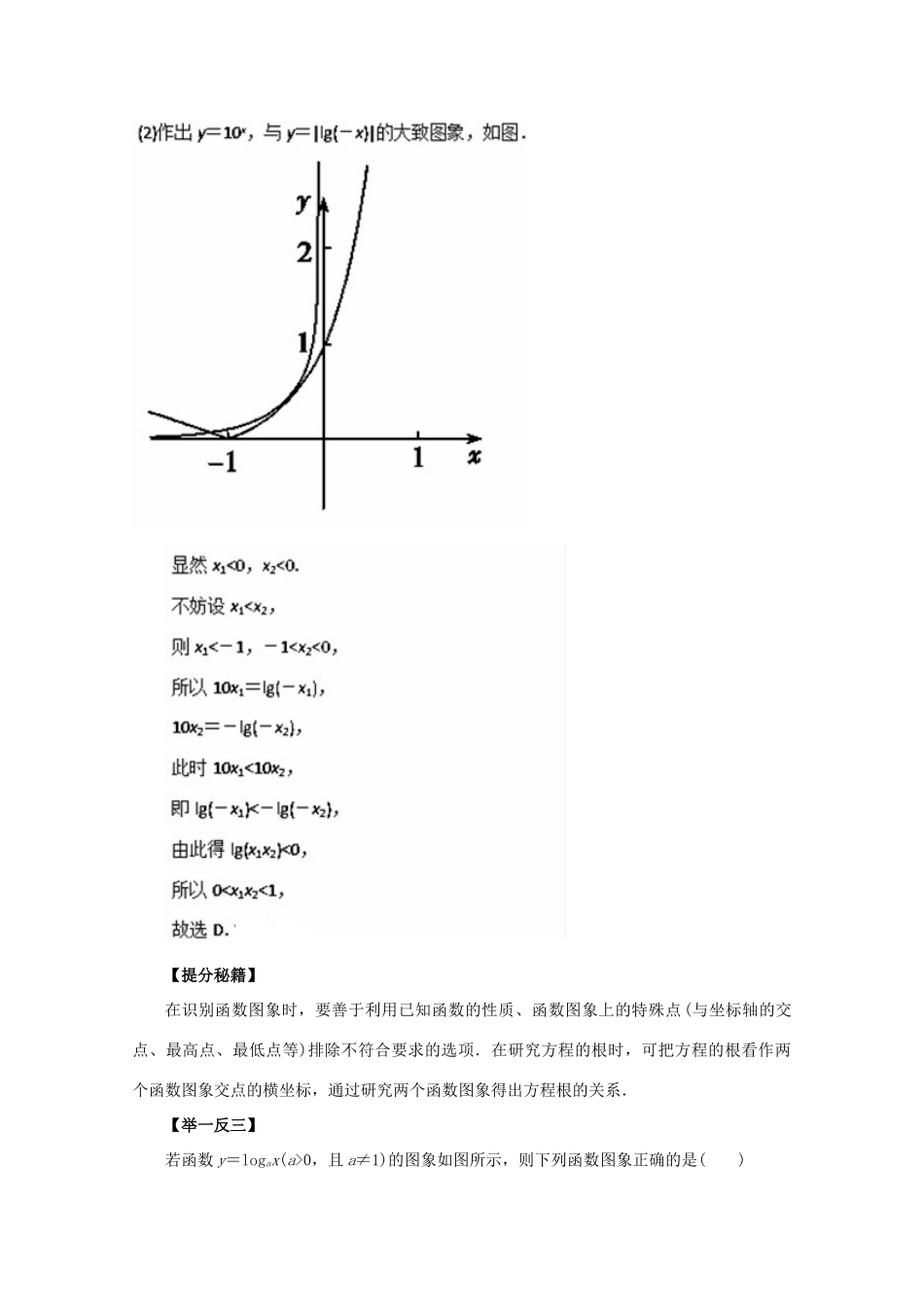
2016年高考数学热点题型和提分秘籍专题09对数与对数函数理(含解析)新人教A版【高频考点解读】1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化为自然对数或常用对数;了解对数在简化运算中的作用.2.理解对数函数的概念,理解对数函数的单调性,掌握对数函数图象通过的特殊点.3.知道对数函数是一类重要的函数模型.4.了解指数函数y=ax与对数函数y=logax互为反函数(a>0,且a≠1).【热点题型】题型一对数运算例1、(1)(+)2log(-)=()A.1B.C.D.(2)=________.(3)若log147=a,14b=5,则a,b表示log3528=________.【答案】(1)D(2)-(3)(3) 14b=5,∴log145=b,又log147=a,∴log3528===.【提分秘籍】对数式的化简与求值的常用思路:(1)先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算法则化简合并.(2)先将对数式化为同底数对数的和、差、倍数的运算,然后逆用对数的运算法则,转化为同底数真数的积、商、幂再运算.【举一反三】lg25+lg2·lg50+(lg2)2=()A.1B.2C.3D.4【答案】B题型二对数函数的图象及应用例2(1)函数f(x)=lg(|x|-1)的大致图象是()(2)设方程10x=|lg(-x)|的两个根分别为x1,x2,则()A.x1x2<0B.x1x2=0C.x1x2>1D.0
0时,f(x)=lg(x-1),将函数y=lgx图象向右平移一个单位得到f(x)=lg(x-1)的图象,再根据对称性可知应选B.解法二由|x|-1>0得x<-1或x>1,可排除C,D;又x>1时f(x)=lg(x-1)在(1,+∞)上是增函数,故排除A选B.【提分秘籍】在识别函数图象时,要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.在研究方程的根时,可把方程的根看作两个函数图象交点的横坐标,通过研究两个函数图象得出方程根的关系.【举一反三】若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是()【答案】B【解析】题型三对数函数的性质及应用例3、对于函数f(x)=log(x2-2ax+3),解答下列问题:(1)若f(x)的定义域为R,求实数a的取值范围;(2)若f(x)的值域为R,求实数a的取值范围;(3)若函数f(x)在(-∞,1]内为增函数,求实数a的取值范围.【解析】设u=g(x)=x2-2ax+3=(x-a)2+3-a2.(1) u>0对x∈R恒成立,∴umin=3-a2>0,∴-0的解集为R得Δ=4a2-12<0求出-0,且a≠1)的图像如图11所示,则下列函数图像正确的是()图11【答案】B(2014·江西卷)已知函数f(x)=5|x|,g(x)=ax2-x(a∈R).若f[g(1)]=1,则a=()A.1B.2C.3D.-1【答案】A【解析】g(1)=a-1,由f[g(1)]=1,得5|a-1|=1,所以|a-1|=0,故a=1.(2014·辽宁卷)已知a=2-,b=log2,c=log,则()A.a>b>cB.a>c>bC.c>a>bD.c>b>a【答案】C【解析】因为0log=1,所以c>a>b.(2014·山东卷)设集合A={x||x-1|<2},B={y|y=2x,x∈[0,2]},则A∩B=()A...