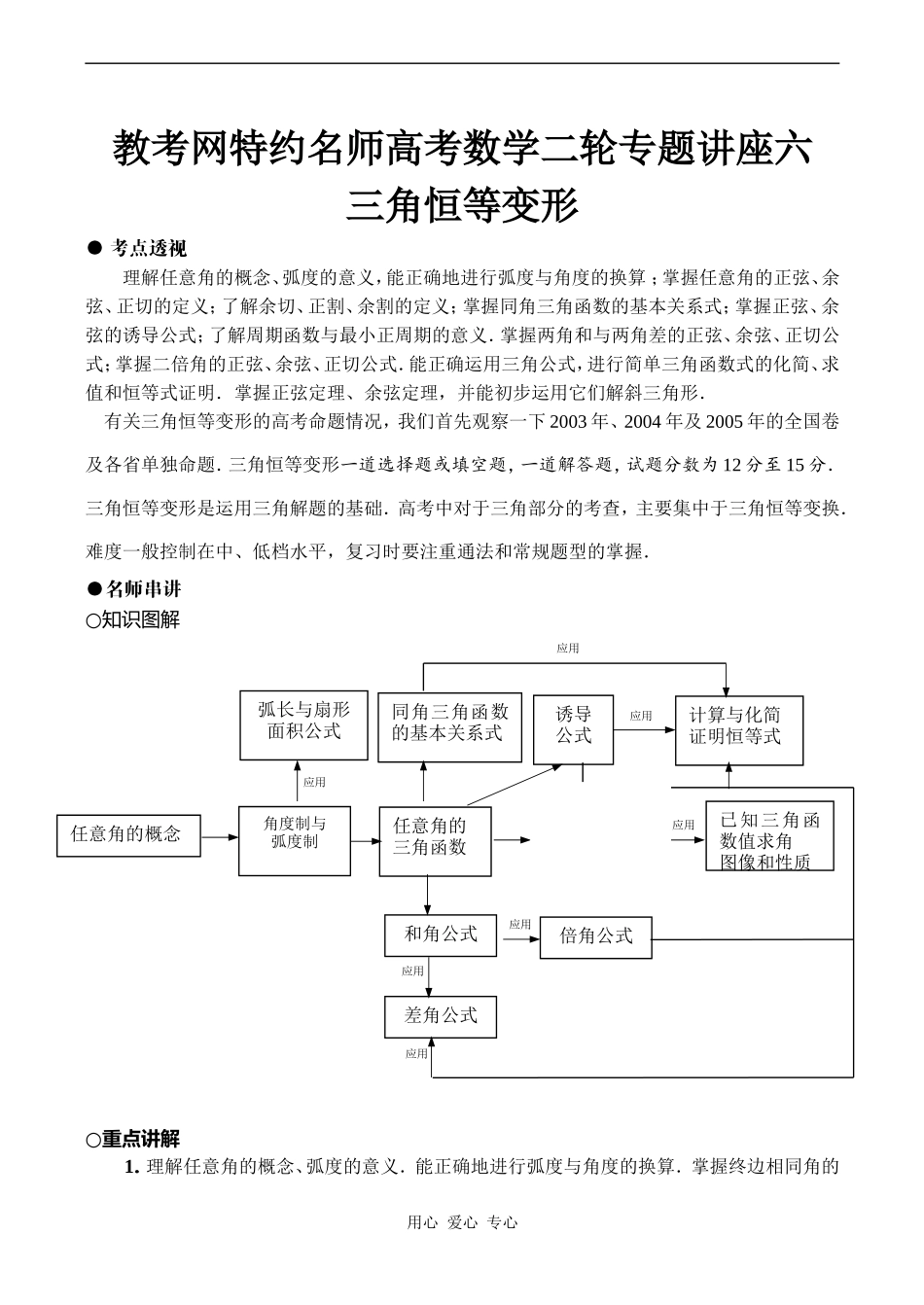
教考网特约名师高考数学二轮专题讲座六三角恒等变形●考点透视理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算;掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义.掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.有关三角恒等变形的高考命题情况,我们首先观察一下2003年、2004年及2005年的全国卷及各省单独命题.三角恒等变形一道选择题或填空题,一道解答题,试题分数为12分至15分.三角恒等变形是运用三角解题的基础.高考中对于三角部分的考查,主要集中于三角恒等变换.难度一般控制在中、低档水平,复习时要注重通法和常规题型的掌握.●名师串讲○知识图解○重点讲解1.理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.掌握终边相同角的用心爱心专心任意角的概念弧长与扇形面积公式角度制与弧度制同角三角函数的基本关系式诱导公式计算与化简证明恒等式任意角的三角函数已知三角函数值求角图像和性质和角公式倍角公式差角公式应用应用应用应用应用应用应用表示方法.掌握任意角的正弦、余弦、正切的意义.了解余切、正割、余割的定义.掌握三角函数的符号法则.理解三角函数线.2.掌握同角三角函数的基本关系式:sin2α+cos2α=1,=tanα,tanαcotα=1,掌握正弦、余弦的诱导公式.能运用化归思想(即将含有较多三角函数名称问题化成含有较少三角函数名称问题)解题.掌握两角和与两角差的正弦、余弦、正切公式,掌握二倍角的正弦、余弦、正切公式,能运用化归思想(将不同角化成同角等)解题.掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式;能灵活运用和角、差角、倍角公式解题.○技巧方法1.注意运用终边相同的角的表示方法表示有关象限角等;已知角的终边上一点的坐标,求三角函数值往往运用定义法;注意运用三角函数线解决有关三角不等式.在三角式的化简,求值等三角恒等变换中,要注意将不同名的三角函数化成同名的三角函数.注意1的作用:如1=sin2θ+cos2θ.要注意观察式子特征,关于sinθ、cosθ的齐次式可转化成关于tanθ的式子.2.审题中,要善于观察已知式和欲求式的差异,注意角之间的关系;整体思想是三角变换中常用的思想.在三角变换中,要注意三角公式的逆用和变形运用,特别要注意如下公式:tanA+tanB=tan(A+B)[1-tanAtanB];asinx+bcosx=sin(x+φ)及升幂、降幂公式的运用.3.证明三角等式的思路和方法.(1)思路:利用三角公式进行化名、化角、改变运算结构,使等式两边化为同一形式.(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法.4.证明三角不等式的方法.比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线、判别法等.●考题解析【例1】(2004年湖南卷类)已知求的值.【思路串讲】本题主要考查三角恒等变形与三角公式以及简单的计算技能.对条件“”可从多方面入手,而对所求“”亦可从多角度思考.不同思维层次的学生,会从不同的角度进行破题,因而不同的解答可显示出答题者不同的能力差异,不同的思维习惯,不同的思考方式,因此本题是全面考查考生发散思维能力的好题.试题属容易题,为在解答题的起始题中继续稳定考生的情绪,起到了积极的作用.试题“”中出现-1,那是为了提示使用余弦的二倍角公式,那是为了减低答题的难度.解题突破口:利用三角恒等变形,化简条件,甚至直接求出角;利用目标分析法,首先对所求表达式进行变形,在逐步缩小它与已知间的差用心爱心专心异,寻找它们之间的联系点,最终确定解题的最佳途径.【标准答案】由==得又,所以.于是===【例2】(2004年全国理Ⅲ)已知α为第二象限角,且sinα=求的值.【思路串讲】本题主要考查同角三角函数的基本关系式,二倍角公式以及三角函数式的恒等变形等...