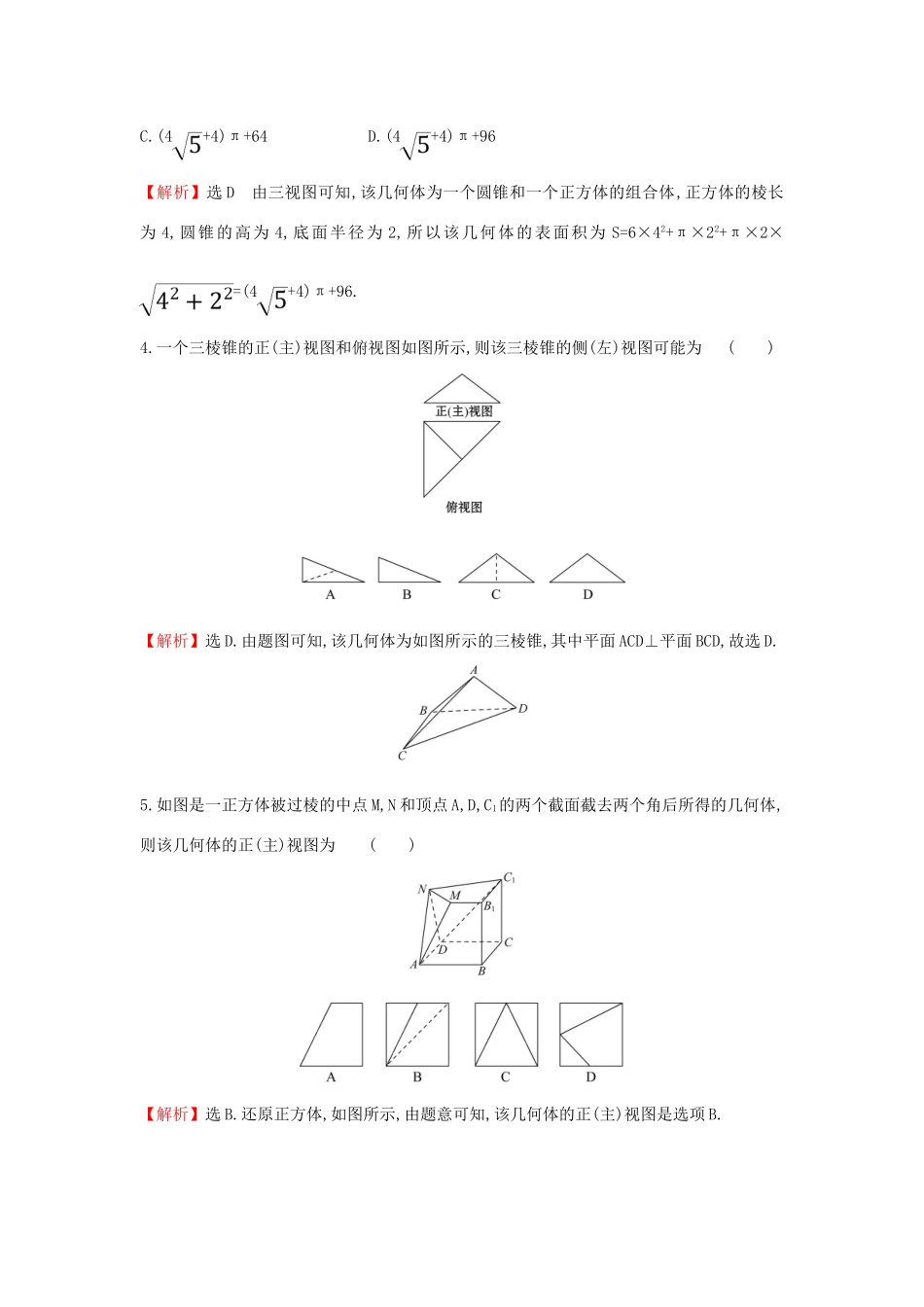
第一讲空间几何体的三视图、表面积及体积(40分钟70分)一、选择题(每小题5分,共25分)1.(2018·北京高考)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.4【命题意图】本小题主要考查空间几何体的三视图,意在考查三视图与直观图的转化,培养学生的空间想象能力,体现了直观想象的数学素养.【解析】选C.将四棱锥三视图转化为直观图,如图,侧面共有4个三角形,即△PAB,△PBC,△PCD,△PAD,由已知,PD⊥平面ABCD,又AD⊂平面ABCD,所以PD⊥AD,同理PD⊥CD,PD⊥AB,所以△PCD,△PAD是直角三角形.因为AB⊥AD,PD⊥AB,PD,AD⊂平面PAD,PD∩AD=D,所以AB⊥平面PAD,又PA⊂平面PAD所以AB⊥PA,△PAB是直角三角形.因为AB=1,CD=2,AD=2,PD=2,所以PA==2,PC==2PB==3,在梯形ABCD中,易知BC=,△PBC三条边长为2,3,,△PBC不是直角三角形.综上,侧面中直角三角形个数为3.2.已知某几何体的三视图如图所示,则该几何体的体积为()A.B.32C.D.【解析】选A.由三视图可知,该几何体是由底面为等腰直角三角形(腰长为4)、高为8的直三棱柱截去一个等底且高为4的三棱锥而得到的,所以该几何体的体积V=×4×4×8-××4×4×4=.3.(2018·湖南五市十校联考)如图,小方格是边长为1的正方形,一个几何体的三视图如图所示,则该几何体的表面积为()A.4π+96B.(2+6)π+96C.(4+4)π+64D.(4+4)π+96【解析】选D由三视图可知,该几何体为一个圆锥和一个正方体的组合体,正方体的棱长为4,圆锥的高为4,底面半径为2,所以该几何体的表面积为S=6×42+π×22+π×2×=(4+4)π+96.4.一个三棱锥的正(主)视图和俯视图如图所示,则该三棱锥的侧(左)视图可能为()【解析】选D.由题图可知,该几何体为如图所示的三棱锥,其中平面ACD⊥平面BCD,故选D.5.如图是一正方体被过棱的中点M,N和顶点A,D,C1的两个截面截去两个角后所得的几何体,则该几何体的正(主)视图为()【解析】选B.还原正方体,如图所示,由题意可知,该几何体的正(主)视图是选项B.二、填空题(每小题5分,共15分)6.若一个几何体的表面积和体积相同,则称这个几何体为“同积几何体”.已知某几何体为“同积几何体”,其三视图如图所示,则a=____________.【解析】根据几何体的三视图可知该几何体是一个四棱柱,如图所示,可得其体积为(a+2a)·a·a=a3,其表面积为·(2a+a)·a·2+a2+a2+2a·a+a·a=7a2+a2,所以7a2+a2=a3,解得a=.答案:7.(2017·全国卷Ⅰ)如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____________.【解析】连接OB,连接OD,交BC于点G,由题意得,OD⊥BC,OG=BC,设OG=x,则BC=2x,DG=5-x,三棱锥的高h===,S△ABC=2x·3x·=3x2,则V=S△ABC·h=x2·=·,令f=25x4-10x5,x∈,f′=100x3-50x4,令f′>0,即x4-2x3<0,x<2,则f≤f=80,则V≤×=4,所以体积最大值为4cm3.答案:4cm38.如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=AB,∠AA1C1=60°,AB⊥AA1,H为CC1的中点,D为BB1的中点.若AB=,则三棱柱ABC-A1B1C1的体积为____________.【解析】连接AC1,可知△ACC1为正三角形,又H为棱CC1的中点,所以AH⊥CC1,从而AH⊥AA1,又平面AA1C1C⊥平面ABB1A1,平面AA1C1C∩平面ABB1A1=AA1,AH⊂平面AA1C1C,所以AH⊥平面ABB1A1,又A1D⊂平面ABB1A1,所以AH⊥A1D①.因为AB=.AC=AA1=AB,所以AC=AA1=2,DB1=1,==,又∠DB1A1=∠B1A1A=90°,所以△A1DB1∽△AB1A1,所以∠B1AA1=∠DA1B1,又∠DA1B1+∠AA1D=90°,所以∠B1AA1+∠AA1D=90°,所以A1D⊥AB1②,由①②及AB1∩AH=A,可得A1D⊥平面AB1H.取AA1的中点M,连接C1M,则C1M∥AH,所以C1M⊥平面ABB1A1,所以=·C1M=××=,所以三棱柱ABC-A1B1C1的体积为3=.答案:三、解答题(每小题10分,共30分)9.如图,边长为的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=AB=1,点M在线段EC上.(1)证明:平面BDM⊥平面ADEF.(2)判断点M的位置,使得三棱锥B-CDM的体积为.【解析】(1)因为DC=BC=1,DC⊥BC,所以BD=.因为AD=,AB=2,所以AD2+BD2=AB2...