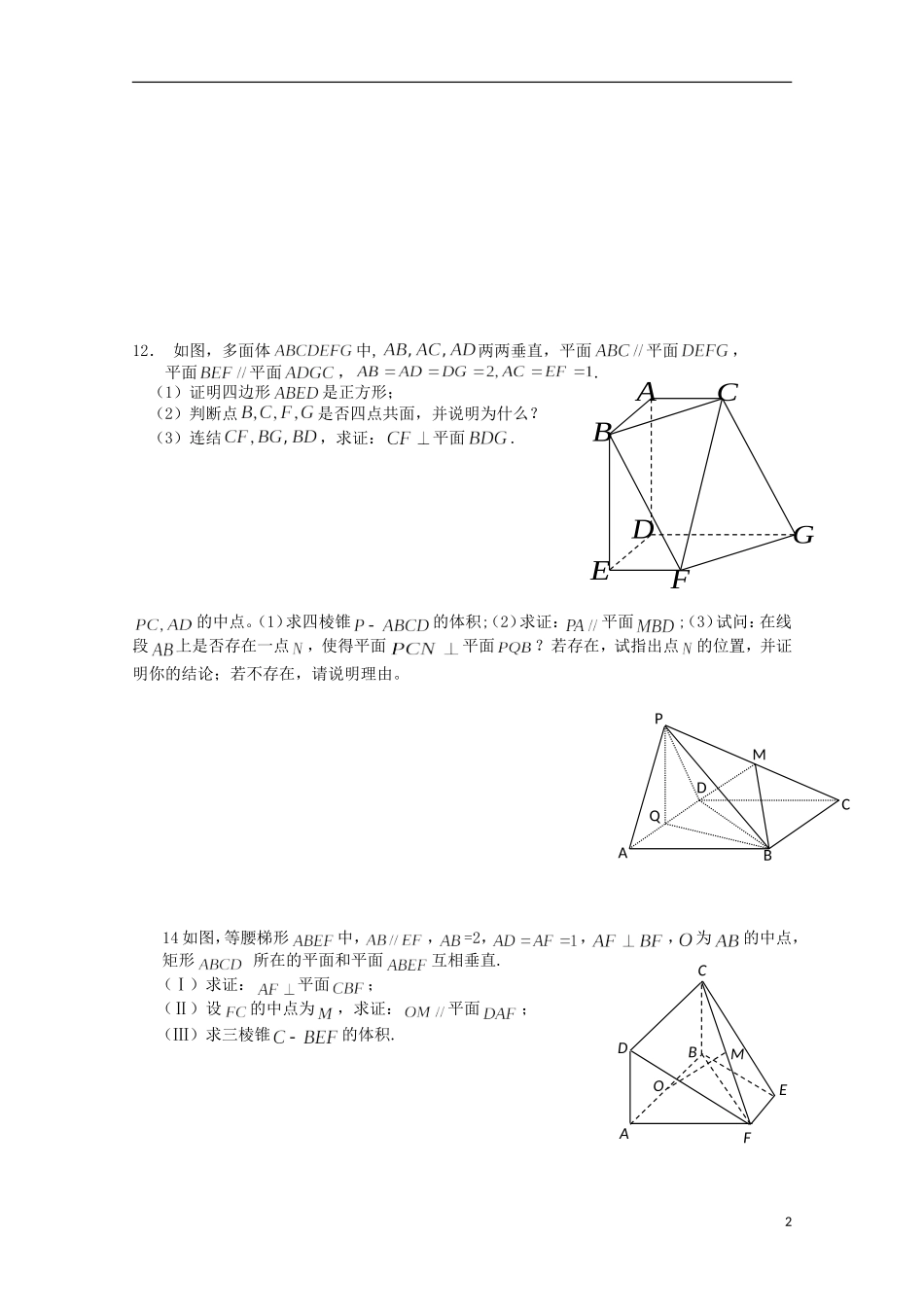
江苏省连云港市田家炳中学高三数学《立体几何》(13)练习1.边长为2的正方体的内切球的表面积为2.AB、CD是两条异面直线,则直线AC、BD的位置关系(填“平行”、“相交”或“异面”).3.设m、n是两条不同的直线,是三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若,则;其中正确命题的序号是.4.一球的表面积与它的体积的数量相等,则球的半径为_____________5.空间四边形中,、分别是、的中点,=3、=4、=,那么与所成角的度数是______6.长方体的长、宽、高之比是1:2:3,对角线长是,则长方体的体积是7.已知直线和平面,下列推理错误的是:.①且②∥且③∥且∥④且∥或8.如图,在正三棱柱中,.若二面角的大小为,则点到平面的距离为.9.在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,EF=,求AD与BC所成角的大小.10.正方体ABCD-A1B1C1D1中,点F为A1D的中点.(1)求证:A1B∥平面AFC;(2)求证:平面A1B1CD平面AFC.11.苏锡常二模如图,在四棱锥中,∥,,,⊥,⊥,为的中点.求证:(1)∥平面;(2)⊥平面.1BACDB1C1D1A1F(第10题)1A1B1CABCDCBAEPQPMDCBA12.如图,多面体中,两两垂直,平面平面,平面平面,.(1)证明四边形是正方形;(2)判断点是否四点共面,并说明为什么?(3)连结,求证:平面.的中点。(1)求四棱锥的体积;(2)求证:平面;(3)试问:在线段上是否存在一点,使得平面平面?若存在,试指出点的位置,并证明你的结论;若不存在,请说明理由。14如图,等腰梯形中,,=2,,,为的中点,矩形所在的平面和平面互相垂直.(Ⅰ)求证:平面;(Ⅱ)设的中点为,求证:平面;(Ⅲ)求三棱锥的体积.2ABCDEFGABCDEFMO3