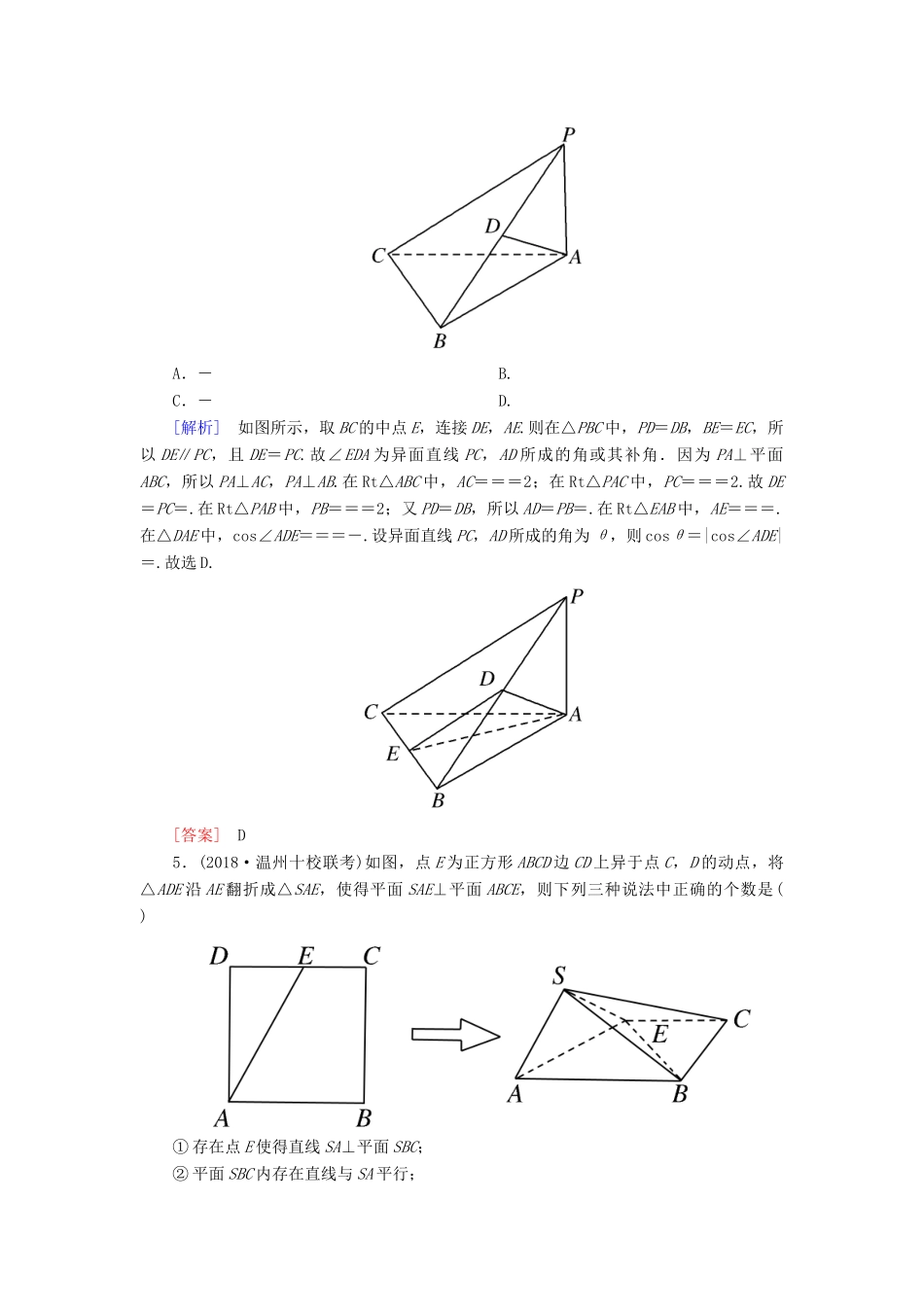
专题跟踪训练(二十二)点、直线、平面之间的位置关系一、选择题1.(2018·中原名校联盟联考)已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是()A.α⊥β且m⊂αB.α⊥β且m∥αC.m∥n且n⊥βD.m⊥n且n∥β[解析]对于选项A,α⊥β且m⊂α,可得m∥β或m与β相交或m⊂β,故A不成立;对于选项B,α⊥β且m∥α,可得m⊂β或m∥β或m与β相交,故B不成立;对于选项C,m∥n且n⊥β,则m⊥β,故C正确;对于选项D,由m⊥n且n∥β,可得m∥β或m与β相交或m⊂β,故D不成立.故选C.[答案]C2.已知直线m,l与平面α,β,γ满足β∩γ=l,l∥α,m⊂α,m⊥γ,则下列命题一定正确的是()A.α⊥γ且l⊥mB.α⊥γ且m∥βC.m∥β且l⊥mD.α∥β且α⊥γ[解析] m⊂α,m⊥γ,∴α⊥γ.又 β∩γ=l,∴l⊂γ,∴l⊥m.故选A.[答案]A3.(2018·内蒙古赤峰模拟)已知三条不重合的直线m,n,l和两个不重合的平面α,β,下列命题中正确命题的个数为()①若m∥n,n⊂α,则m∥α;②若l⊥α,m⊥β且l⊥m,则α⊥β;③若l⊥n,m⊥n,则l∥m;④若α⊥β,α∩β=m,n⊂β,n⊥m,则n⊥α.A.1B.2C.3D.4[解析]①若m∥n,n⊂α,则m∥α或m⊂α,不正确;②若l⊥α,m⊥β,且l⊥m,由面面垂直的判定定理可得α⊥β,正确;③若l⊥n,m⊥n,则l与m平行、相交或为异面直线,不正确;④若α⊥β,α∩β=m,n⊂β,n⊥m,由面面垂直的性质定理得n⊥α,因此正确.综上可知只有②④正确.故选B.[答案]B4.[原创题]如图所示,三棱锥P-ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为()A.-B.C.-D.[解析]如图所示,取BC的中点E,连接DE,AE.则在△PBC中,PD=DB,BE=EC,所以DE∥PC,且DE=PC.故∠EDA为异面直线PC,AD所成的角或其补角.因为PA⊥平面ABC,所以PA⊥AC,PA⊥AB.在Rt△ABC中,AC===2;在Rt△PAC中,PC===2.故DE=PC=.在Rt△PAB中,PB===2;又PD=DB,所以AD=PB=.在Rt△EAB中,AE===.在△DAE中,cos∠ADE===-.设异面直线PC,AD所成的角为θ,则cosθ=|cos∠ADE|=.故选D.[答案]D5.(2018·温州十校联考)如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三种说法中正确的个数是()①存在点E使得直线SA⊥平面SBC;②平面SBC内存在直线与SA平行;③平面ABCE内存在直线与平面SAE平行.A.0B.1C.2D.3[解析]由题图,得SA⊥SE,若存在点E使得直线SA⊥平面SBC,则SA⊥SB,SA⊥SC,则SC,SB,SE三线共面,则点E与点C重合,与题设矛盾,故①错误;因为SA与平面SBC相交,所以在平面SBC内不存在直线与SA平行,故②错误;显然,在平面ABCE内,存在直线与AE平行,由线面平行的判定定理得平面ABCE内存在直线与平面SAE平行,故③正确.选B.[答案]B6.(2018·河北五校联考)在长方体ABCD-A1B1C1D1中,AB=AD=4,AA1=2.过点A1作平面α与AB,AD分别交于M,N两点,若AA1与平面α所成的角为45°,则截面A1MN面积的最小值是()A.2B.4C.4D.8[解析]如图,过点A作AE⊥MN,连接A1E, A1A⊥平面ABCD,∴A1A⊥MN,又 A1A∩AE=A,∴MN⊥平面A1AE,∴A1E⊥MN,平面A1AE⊥平面A1MN,∴∠AA1E为AA1与平面A1MN所成的角,∴∠AA1E=45°,在Rt△A1AE中, AA1=2,∴AE=2,A1E=2,在Rt△MAN中,由射影定理得ME·EN=AE2=4,由基本不等式得MN=ME+EN≥2=4,当且仅当ME=EN,即E为MN的中点时等号成立,∴截面A1MN面积的最小值为×4×2=4,故选B.[答案]B二、填空题7.(2018·定州二模)如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=________.[解析]根据题意,因为EF∥平面AB1C,EF⊂平面ABCD,平面ABCD∩平面AB1C=AC,所以EF∥AC.又E是AD的中点,所以F是CD的中点.因为在Rt△DEF中,DE=DF=1,故EF=.[答案]8.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.[解析]过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面...