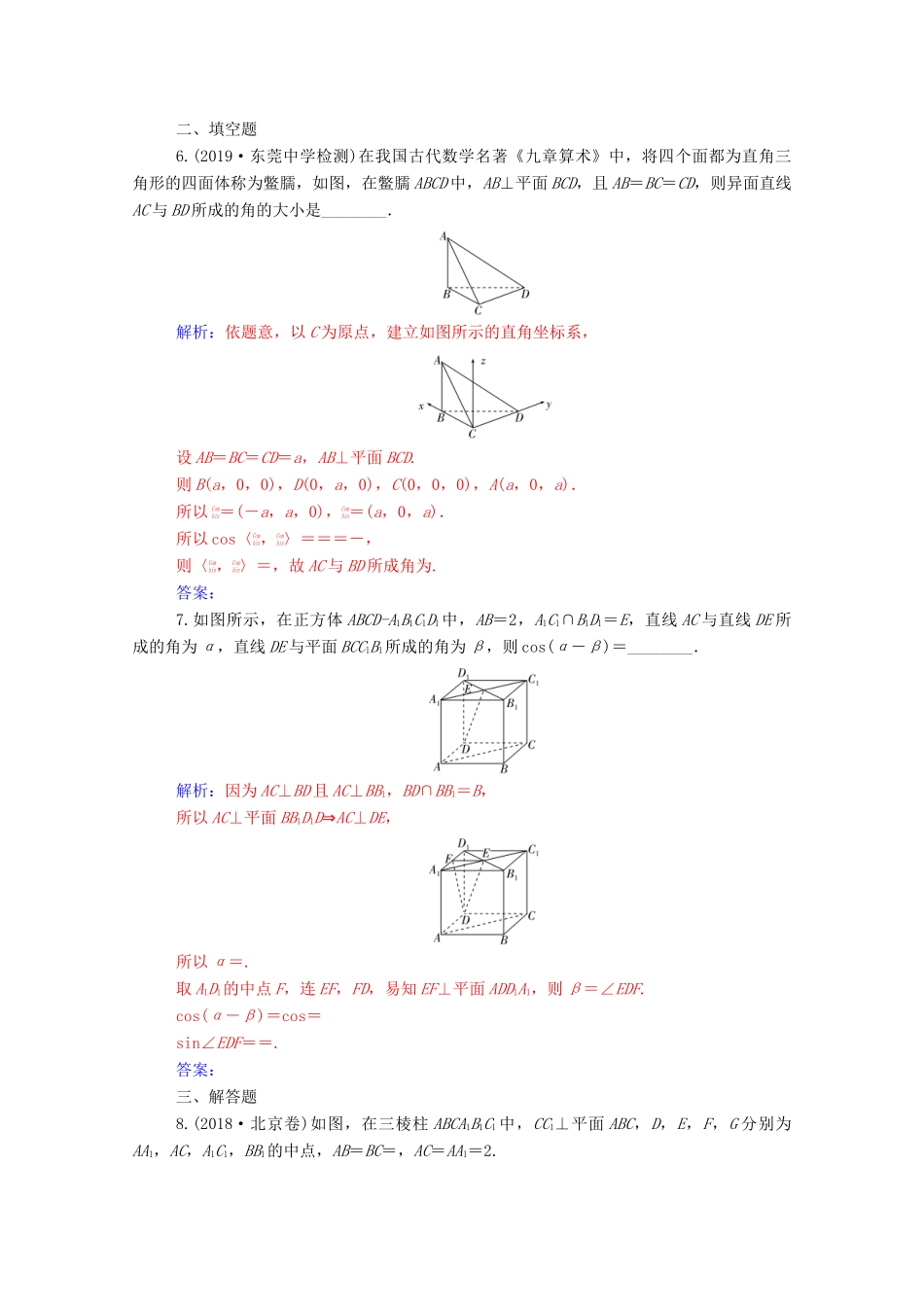
第3讲立体几何中的向量方法A级基础通关一、选择题1.如图,F是正方体ABCD-A1B1C1D1的棱CD的中点.E是BB1上一点,若D1F⊥DE,则有()A.B1E=EBB.B1E=2EBC.B1E=EBD.E与B重合解析:以D为坐标原点,以DA,DC,DD1所在直线为坐标轴建立坐标系,设正方体的棱长为2,则D(0,0,0),F(0,1,0),D1(0,0,2),设E(2,2,z),则Combin=(0,1,-2),Combin=(2,2,z),因为Combin·Combin=0×2+1×2-2z=0,所以z=1,所以B1E=EB.答案:A2.如图,点A,B,C分别在空间直角坐标系O-xyz的三条坐标轴上,Combin=(0,0,2),平面ABC的法向量为n=(2,1,2),设二面角C-AB-O的大小为θ,则cosθ等于()A.B.C.D.-解析:由题意可知,平面ABO的一个法向量为Combin=(0,0,2),由图可知,二面角C-AB-O为锐角,由空间向量的结论可知,cosθ===.答案:C3.在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值是()A.B.C.D.解析:如图,建立空间直角坐标系,易求点D,平面AA1C1C的一个法向量是n=(1,0,0),所以sinα=|cos〈n,Combin〉|==.答案:D4.如图所示,在平行六面体ABCD-A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则:①A1M∥D1P;②A1M∥B1Q;③A1M∥平面DCC1D1;④A1M∥平面D1PQB1.以上说法正确的个数为()A.1B.2C.3D.4解析:Combin=Combin+Combin=Combin+Combin,Combin=Combin+Combin=Combin+Combin,所以Combin∥Combin,所以A1M∥D1P,由线面平行的判定定理可知,A1M∥平面DCC1D1,A1M∥平面D1PQB1.①③④正确.答案:C5.(2018·全国卷Ⅱ)在长方体ABCDA1B1C1D1中,AB=BC=1,AA1=,则异面直线AD1与DB1所成角的余弦值为()A.B.C.D.解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示.由条件可知D(0,0,0),A(1,0,0),D1(0,0,),B1(1,1,),所以Combin=(-1,0,),Combin=(1,1,).则cos〈Combin,Combin〉===.故异面直线AD1与DB1所成角的余弦值为.答案:C二、填空题6.(2019·东莞中学检测)在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成的角的大小是________.解析:依题意,以C为原点,建立如图所示的直角坐标系,设AB=BC=CD=a,AB⊥平面BCD.则B(a,0,0),D(0,a,0),C(0,0,0),A(a,0,a).所以Combin=(-a,a,0),Combin=(a,0,a).所以cos〈Combin,Combin〉===-,则〈Combin,Combin〉=,故AC与BD所成角为.答案:7.如图所示,在正方体ABCD-A1B1C1D1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=________.解析:因为AC⊥BD且AC⊥BB1,BD∩BB1=B,所以AC⊥平面BB1D1D⇒AC⊥DE,所以α=.取A1D1的中点F,连EF,FD,易知EF⊥平面ADD1A1,则β=∠EDF.cos(α-β)=cos=sin∠EDF==.答案:三、解答题8.(2018·北京卷)如图,在三棱柱ABCA1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角BCDC1的余弦值;(3)证明:直线FG与平面BCD相交.(1)证明:在三棱柱ABCA1B1C1中,因为CC1⊥平面ABC,所以四边形A1ACC1为矩形.又E,F分别为AC,A1C1的中点,所以AC⊥EF.因为AB=BC,所以AC⊥BE.又EF∩BE=E,所以AC⊥平面BEF.(2)解:由(1)知AC⊥EF,AC⊥BE,EF∥CC1.又CC1⊥平面ABC,所以EF⊥平面ABC.因为BE⊂平面ABC,所以EF⊥BE.如图建立空间直角坐标系Exyz.由题意得B(0,2,0),C(-1,0,0),D(1,0,1),E(0,0,0),F(0,0,2),G(0,2,1).所以Combin=(-1,-2,0),Combin=(1,-2,1).设平面BCD的法向量为n=(x0,y0,z0).则即令y0=-1,则x0=2,z0=-4.于是n=(2,-1,-4).又因为平面CC1D的法向量为Combin=(0,2,0),所以cos〈n,Combin〉==-.由题意知二面角BCDC1为钝角,所以其余弦值为-.(3)证...