湖北省武汉二中、仙桃中学08-09学年度高一数学上学期期末联考【会员独享】VIP免费

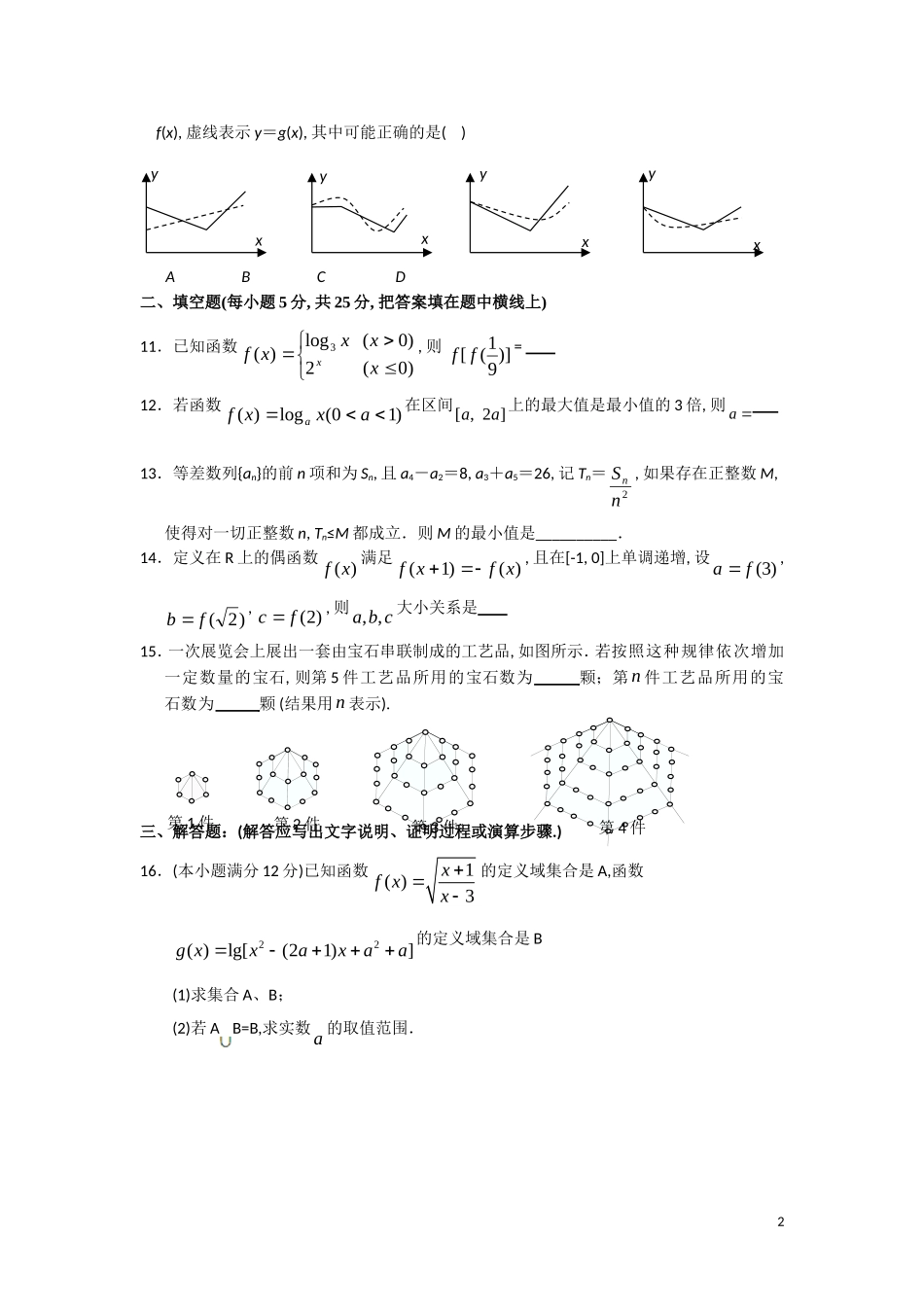
仙桃中学、武汉二中2008—2009学年度上学期期末联考高一年级数学期末试卷一、选择题：(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1．设全集U=R,A={xN∈︱1≤x≤10},B={xR∈︱x2+x－6=0},则下图中阴影表示的集合为()A．{2}B．{3}C．{－3,2}D．{－2,3}2．已知命题p、q,则“命题p或q为真”是“命题p且q为真”的()A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．计算机的价格大约每３年下降,那么今年花8100元买的一台计算机,９年后的价格大约是()A.2400元B.900元C.300元D.100元4．设函数y＝f(x)的反函数为y＝1()fx,且y＝f(2x－1)的图象过点(12,1),则y＝1()fx的图像必过()．A．(12,1)B．(1,12)C．(1,0)D．(0,1)5．已知数列na的前n项和29nSnn,第k项满足58ka,则k等于()A．9B．8C．7D．66函数11231xy值域为()A．(-∞,1)B．(31,1)C．[31,1)D．[31,+∞)7．已知数列{an}是等比数列,且每一项都是正数,若a2,a48是2x2－7x+6=0的两个根,则a1·a2·a25·a48·a49的值为()A．221B．93C．±93D．358．已知等差数列{}na的公差0d,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是()A．4B．3C．2D．129．若关于x的方程4x+2xbc=0有2个不同的实数解,则b,c的符号为()A．b>0,c>0B．b>0,c<0C．b<0,c>0D．b<0,c<010．在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y＝f(x),一种是平均价格曲线y＝g(x)(如f(2)＝3表示开始交易后第2小时的即时价格为3元；g(2)＝4表示开始交易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示y＝1第1件第2件第3件第4件f(x),虚线表示y＝g(x),其中可能正确的是()ABCD二、填空题(每小题5分,共25分,把答案填在题中横线上)11．已知函数)0(2)0(log)(3xxxxfx,则)]91([ff=12．若函数)10(log)(axxfa在区间[,2]aa上的最大值是最小值的3倍,则a13．等差数列{an}的前n项和为Sn,且a4－a2＝8,a3＋a5＝26,记Tn＝2nSn,如果存在正整数M,使得对一切正整数n,Tn≤M都成立．则M的最小值是__________．14．定义在R上的偶函数)(xf满足)()1(xfxf,且在[-1,0]上单调递增,设)3(fa,)2(fb,)2(fc,则cba,,大小关系是15．一次展览会上展出一套由宝石串联制成的工艺品,如图所示．若按照这种规律依次增加一定数量的宝石,则第5件工艺品所用的宝石数为颗；第n件工艺品所用的宝石数为颗(结果用n表示).三、解答题：(解答应写出文字说明、证明过程或演算步骤.)16．(本小题满分12分)已知函数1()3xfxx的定义域集合是A,函数22()lg[(21)]gxxaxaa的定义域集合是B(1)求集合A、B；(2)若AB=B,求实数a的取值范围．2xxxxyyyy17．(本小题满分12分)当[1,1)x时,求xxaxf432)(2)3(a的最小值.18.(本小题满分12分)已知数列{an}满足递推关系式133(2)nnnaan,其中381a.(1)求a1,a2；(2)求证：数列{}3nna为等差数列；(3)求数列{an}的前n项和Sn.319．(本小题满分12分)已知函数()log()(0,1)afxaxxaa(1)求函数f(x)的定义域；(2)若a=2,判断f(x)在定义域上的单调性并加以证明.20．(本小题满分1３分)某工厂在“减员增效”工作中,规定下岗人员第一年可以到原单位领取全额工资,从第二年起,以后每年只能在原单位按上一年工资额的43领取.该工厂根据下岗人员特长,创办新的经济实体.该实体预计第一年属投资阶段,没有利润,因而职员均无收入.第二年每人年收入可达b元,从第三年起每人年收入可在上一年的基础上递增31.如果某工人下岗后立即转入这个创办的经济实体,又设该工人下岗前的年工资额为a元.(1)求这位工人下岗后第n年的年收入an的表达式；(2)当b＝(43)5a时,这位工人哪一年的收入最少?最少年收入是多少?21．(本小题满分14分)设函数f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,yR,∈有f(x+y)=f(x)·f(y).(1)求f(0),判断并证明函数f(x)的单调性；(2)Sn为数列{}na的前n项和,已知1(0)af,且1()(2)nnfSfna.①求数列{}na的通项公式；②已知11115,11nannnnbcbb,数列{}nc的前n项和为nT,求证：...