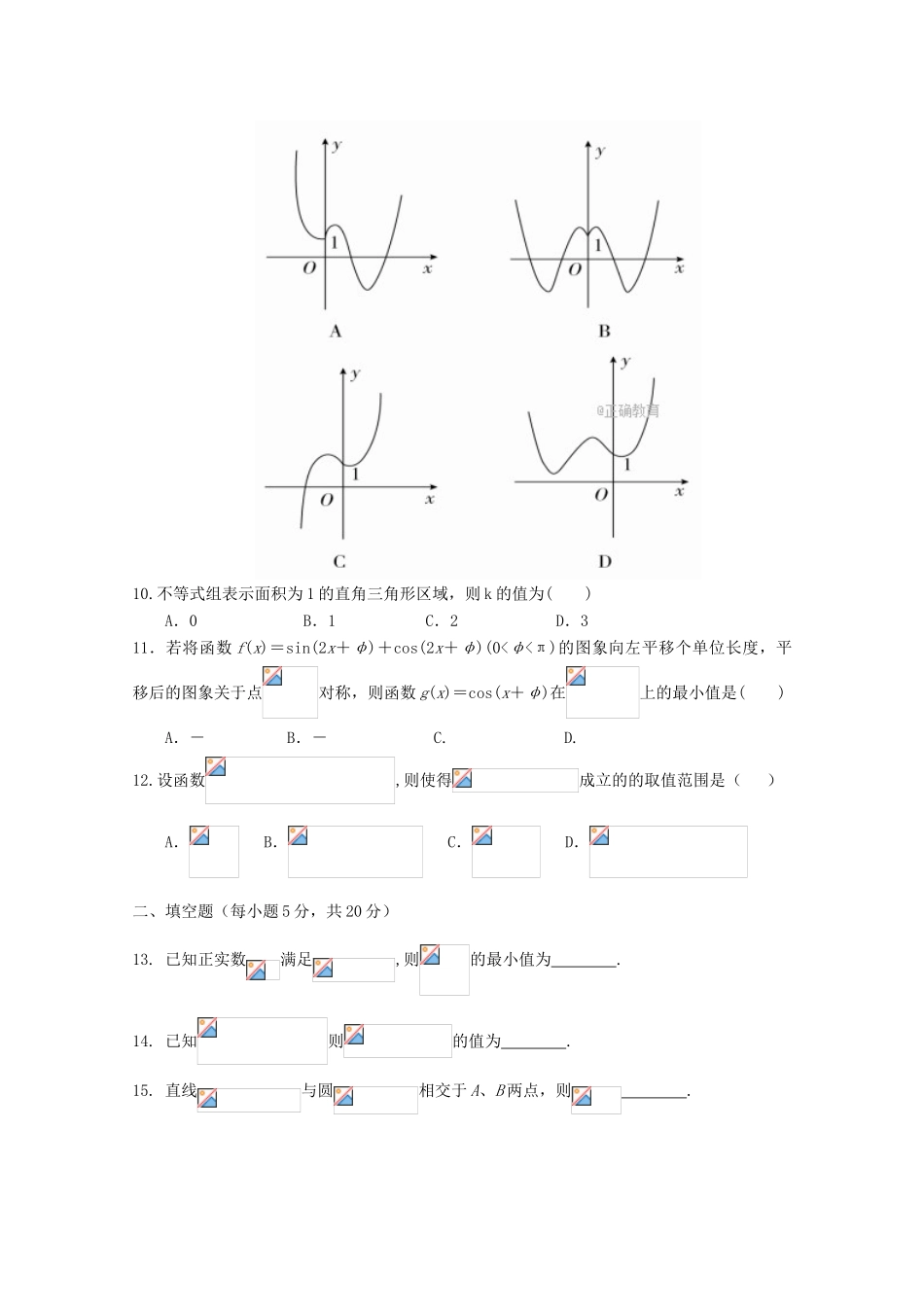
2017-2018学年第一学期第三次月考高三年级文科数学试题本试卷满分为150分,考试时间为120分钟。第Ⅰ卷(选择题共60分)一、选择题(在下列各题的四个选项中,只有一个是最符合题意的。每小题5分,共60分。)1.已知集合,则()A.B.C.D.2.已知i为虚数单位,复数z的共轭复数为,且满足2z+=3-2i,则z=()A.l-2iB.l+2iC.2-iD.2+i3.已知向量,,且,则的值为()A.B.C.D.4.直线y=kx+2与圆x2+y2=1没有公共点的充要条件是()A.k∈(-,)B.k∈(-∞,-)∪(,+∞)C.k∈(-,)D.k∈(-∞,-)∪(,+∞)5.若,,,则()A.B.C.D.6.函数的单调递增区间是()A.B.C.D.7.已知P是△ABC所在平面外的一点,M、N分别是AB、PC的中点,若MN=BC=4,PA=4,则异面直线PA与MN所成角的大小是()A.30°B.45°C.60°D.90°8.设F1,F2分别是椭圆+=1的左、右焦点,P为椭圆上一点,M是F1P的中点,|OM|=3,则P点到椭圆左焦点的距离为()A.4B.3C.2D.59.函数y=e|x|-x3的大致图象是()10.不等式组表示面积为1的直角三角形区域,则k的值为()A.0B.1C.2D.311.若将函数f(x)=sin(2x+φ)+cos(2x+φ)(0<φ<π)的图象向左平移个单位长度,平移后的图象关于点对称,则函数g(x)=cos(x+φ)在上的最小值是()A.-B.-C.D.12.设函数,则使得成立的的取值范围是()A.B.C.D.二、填空题(每小题5分,共20分)13.已知正实数满足,则的最小值为.14.已知则的值为.15.直线与圆相交于A、B两点,则.16.已知函数若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是三、解答题(17题10分,18-22题,每题12分,共70分)17.(本小题满分10分)已知在中,角所对的边分别为已知(Ⅰ)求的值;(Ⅱ)若,求的面积18.(本小题满分12分)已知数列的首项为,且.(Ⅰ)求证:数列是等比数列,并求数列的通项公式;(Ⅱ)若,求数列的前项和.19.(本小题满分12分)如图,在四棱锥中,侧棱底面,底面为矩形,,为上一点,且.(1)若为的中点,求证:平面;(2)求三棱锥的体积.20.(本小题满分12分)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点。(1)求M的轨迹方程;(2)当|OP|=|OM|时,求l的方程及△POM的面积.21.(本小题满分12分)已知椭圆C的焦点坐标是F1(-1,0)、F2(1,0),过点F2垂直于长轴的直线l交椭圆C于B、D两点,且|BD|=3.(1)求椭圆C的方程;(2)是否存在过点P(2,1)的直线l1与椭圆C相交于不同的两点M、N,且满足PM·PN=?若存在,求出直线l1的方程;若不存在,请说明理由.22.(本小题满分12分)已知函数,函数,函数的导函数为.(1)求函数的极值;(2)若,(i)求函数的单调区间;(ii)求证:时,不等式恒成立.集宁一中2017-2018学年第一学期第三次月考高三年级文科数学试题答案选择题:1-6CABCAD7-12AAABDA13.14.15.216.17、(12分)【答案】(Ⅰ);(Ⅱ).(Ⅰ)因为所以所以又故,故,由正弦定理可得(Ⅱ)由(Ⅰ)可得,联立,解得.由,得为直角三角形,所以18.解:(Ⅰ)由得,…………2分则数列是以3为首项,以2为公比的等比数列,…………4分可得,从而.…………6分(Ⅱ)依题意,,…………8分故,…………9分故.…………12分19.解:(1)连结BD交AC于O,连结OE, 为的上一点,且,又 F为PE的中点,∴E为DF中点,OE//BF,又 平面AEC∴平面AEC(2)侧棱底面,,又,,∴,又,∴20.解析:(1)圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4。设M(x,y),则CM=(x,y-4),MP=(2-x,2-y)。由题设知CM·MP=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2。由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2。(2)由(1)可知M的轨迹是以点N(1,3)为圆心,为半径的圆。由于|OP|=|OM|,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM。因为ON的斜率为3,所以l的斜率为-,故l的方程为y=-x+。又|OM|=|OP|=2,O到l的距离为,|PM|=,所以△POM的面积为。21.解(1)设椭圆的方程是+=1(a>b>0),则c=1, |BD|=3,∴=3,又a2-b2=1,∴a=2,b=,∴椭圆C的方程为+=1.(4分)(2...