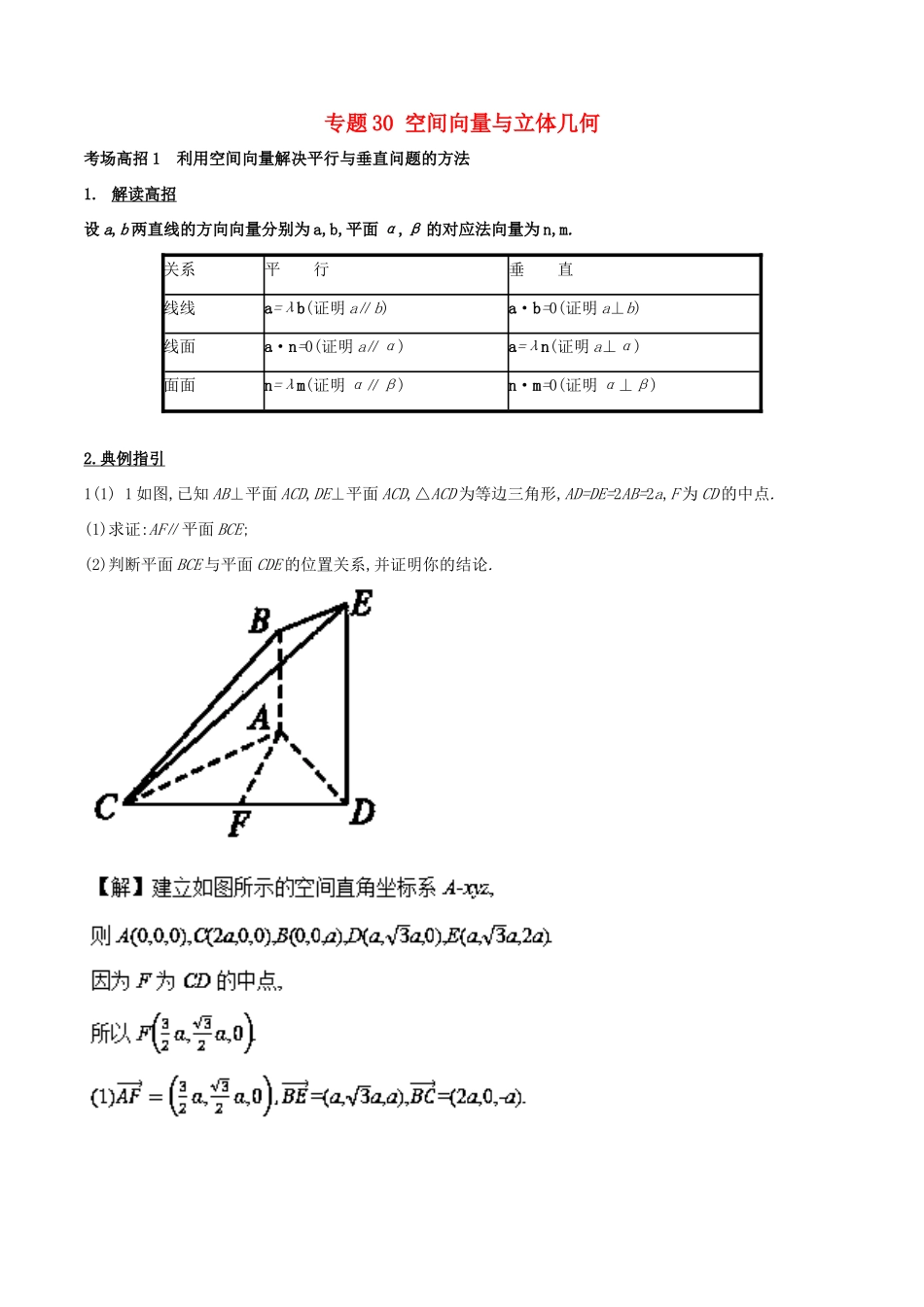
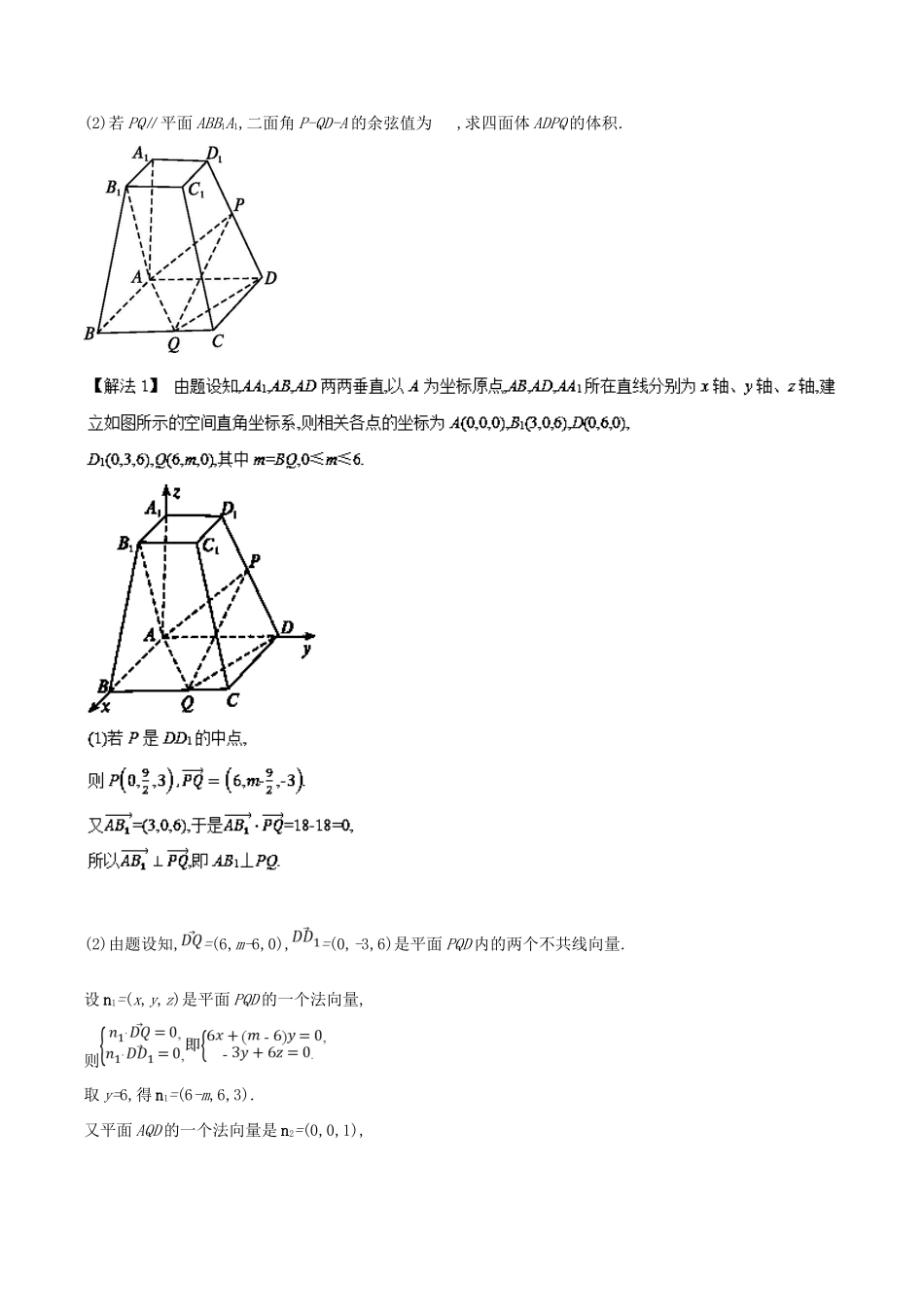
专题30空间向量与立体几何考场高招1利用空间向量解决平行与垂直问题的方法1.解读高招设a,b两直线的方向向量分别为a,b,平面α,β的对应法向量为n,m.关系平行垂直线线a=λb(证明a∥b)a·b=0(证明a⊥b)线面a·n=0(证明a∥α)a=λn(证明a⊥α)面面n=λm(证明α∥β)n·m=0(证明α⊥β)2.典例指引1(1)1如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.(1)求证:AF∥平面BCE;(2)判断平面BCE与平面CDE的位置关系,并证明你的结论.D.a>b>c考场高招32运用空间向量解决立体几何问题的步骤1.解读高招步骤解读建系根据题中的几何图形的特征建立适当的空间直角坐标系定坐标确定点的坐标进而求出有关向量的坐标向量运算进行相关的空间向量的运算翻译将向量中的语言“翻译”成相应的立体几何中的语言,完成几何问题的求解温馨提醒在建立空间直角坐标系求点的坐标时,要使尽可能多的点落在坐标轴上,尽可能多的线段平行于坐标轴,有直角的,把直角边放在坐标轴上2.典例指引2.如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,A1A=6,且A1A⊥底面ABCD,点P,Q分别在棱DD1,BC上.(1)若P是DD1的中点,证明:AB1⊥PQ.(2)若PQ∥平面ABB1A1,二面角P-QD-A的余弦值为,求四面体ADPQ的体积.(2)由题设知,=(6,m-6,0),=(0,-3,6)是平面PQD内的两个不共线向量.设n1=(x,y,z)是平面PQD的一个法向量,则取y=6,得n1=(6-m,6,3).又平面AQD的一个法向量是n2=(0,0,1),所以cos
==.而二面角P-QD-A的余弦值为,因此,解得m=4,或m=8(舍去),此时Q(6,4,0).设=λ(0<λ≤1),而=(0,-3,6),由此得点P(0,6-3λ,6λ),所以=(6,3λ-2,-6λ).因为PQ∥平面ABB1A1,且平面ABB1A1的一个法向量是n3=(0,1,0),所以·n3=0,即3λ-2=0,亦即λ=,从而P(0,4,4).于是,将四面体ADPQ视为以△ADQ为底面的三棱锥P-ADQ,则其高h=4.故四面体ADPQ的体积V=S△ADQ·h=×6×6×4=24(2)如图,过点P作PM∥A1A交AD于点M,则PM∥平面ABB1A1.②因为A1A⊥平面ABCD,所以PM⊥平面ABCD.过点M作MN⊥QD于点N,连接PN,则PN⊥QD,∠PNM为二面角P-QD-A的平面角,所以cos∠PNM=,即,从而.连接MQ,由PQ∥平面ABB1A1及②知,平面PQM∥平面ABB1A1,所以MQ∥AB.又ABCD是正方形,所以ABQM为矩形,故MQ=AB=6.设MD=t,则MN=.④过点D1作D1E∥A1A交AD于点E,则AA1D1E为矩形,所以D1E=A1A=6,AE=A1D1=3,因此ED=AD-AE=3.于是=2,所以PM=2MD=2t.再由③,④得,解得t=2,因此PM=4.故四面体ADPQ的体积V=S△ADQ·PM=×6×6×4=24.3.亲临考场(2014重庆,理19)如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=,M为BC上一点,且BM=,MP⊥AP.(1)求PO的长;(2)求二面角A-PM-C的正弦值.(2)由(1)知,,.设平面APM的法向量为n1=(x1,y1,z1),平面PMC的法向量为n2=(x2,y2,z2),由n1·=0,n1·=0,得故可取n1=,由n2·=0,n2·=0,得故可取从而法向量n1,n2的夹角的余弦值为cos==-,故所求二面角A-PM-C的正弦值为.考点69利用空间向量求空间角考场高招3三法(定义法、间接法、向量法)搞定线面角1.解读高招方法解读适合题型典例指引定义法利用面面垂直的性质定理,得到线面垂直,进而确定线面角中的垂足.明确斜线在平面内的射影,即可确定线面角垂足位置易确定,顺利找到线面角典例导引3(1)几何法在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h,而不必画出线面角,利用sinθ=进行求角垂足位置不易确定,线面角不好找典例导引3(2)方法一向量法借助直线的方向向量与平面的法向量所成的角求直线与平面所成的角.如图所示,设l为平面α的斜线,l∩α=A,a为l的方向向量,n为平面α的法向量,φ为l与α所成的角,则能够顺利建立空间直角坐标系,各点坐标容易确定典例导引3(2)方法二sinφ=|cos|=2.典例指引2(1)3(1)在三棱锥P-ABC中,PA=PB=PC=12,∠ACB=30°,AB=6,则PB与平面ABC所成角的余弦值为;(2)正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的正弦值为.(方法二:向量法)如图,取AC的中点为坐标原点,建立空间直角坐标系.设各棱长为2,则A(0,-1,0),D(0,0,2),C(0,1,0),B1(,0,2).设n=(x,y,z)为平面B1CD的法向量,则取n=(0,2,1).故cos<,n>=,即所求角的正弦...