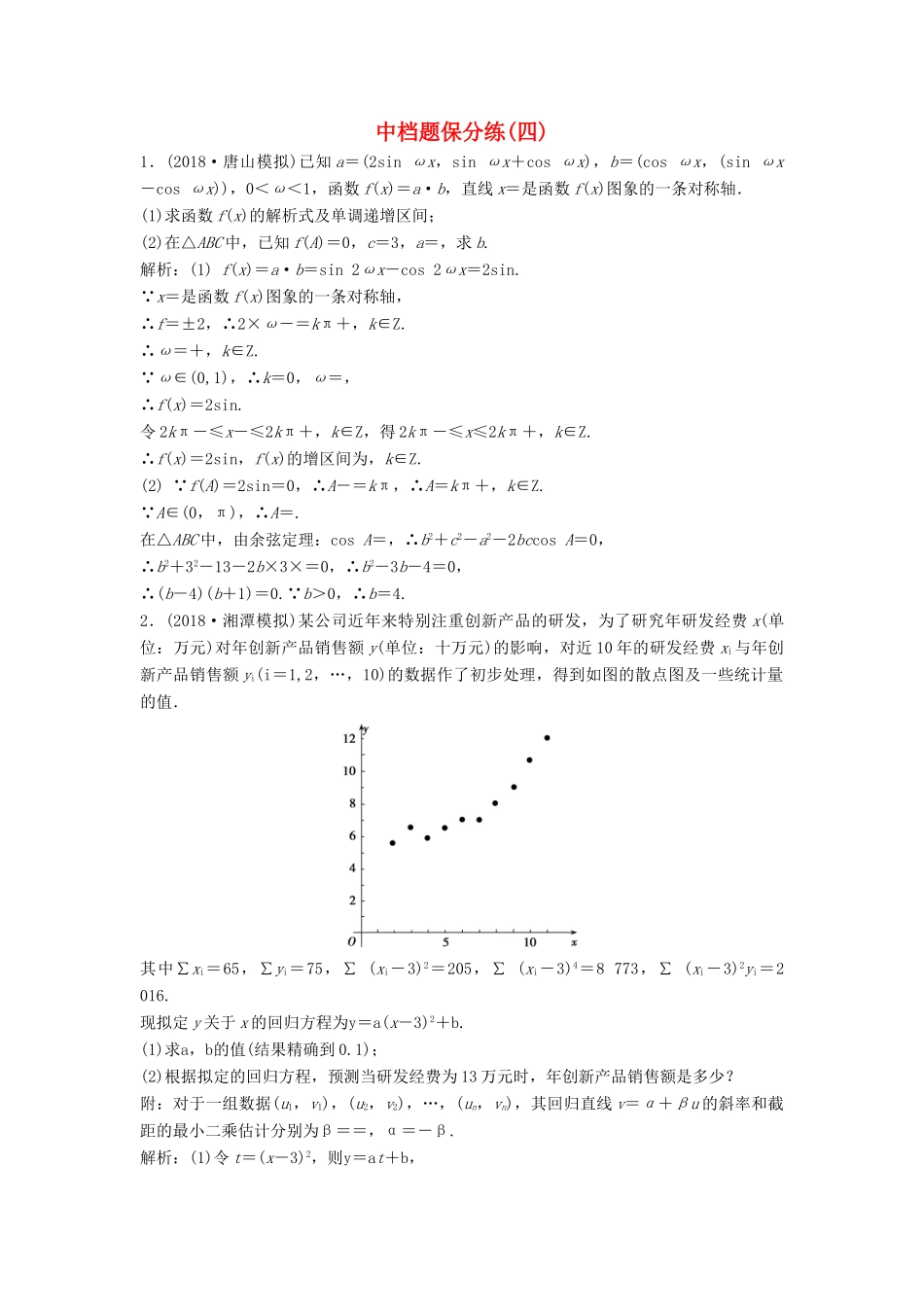
中档题保分练(四)1.(2018·唐山模拟)已知a=(2sinωx,sinωx+cosωx),b=(cosωx,(sinωx-cosωx)),0<ω<1,函数f(x)=a·b,直线x=是函数f(x)图象的一条对称轴.(1)求函数f(x)的解析式及单调递增区间;(2)在△ABC中,已知f(A)=0,c=3,a=,求b.解析:(1)f(x)=a·b=sin2ωx-cos2ωx=2sin.∵x=是函数f(x)图象的一条对称轴,∴f=±2,∴2×ω-=kπ+,k∈Z.∴ω=+,k∈Z.∵ω∈(0,1),∴k=0,ω=,∴f(x)=2sin.令2kπ-≤x-≤2kπ+,k∈Z,得2kπ-≤x≤2kπ+,k∈Z.∴f(x)=2sin,f(x)的增区间为,k∈Z.(2)∵f(A)=2sin=0,∴A-=kπ,∴A=kπ+,k∈Z.∵A∈(0,π),∴A=.在△ABC中,由余弦定理:cosA=,∴b2+c2-a2-2bccosA=0,∴b2+32-13-2b×3×=0,∴b2-3b-4=0,∴(b-4)(b+1)=0.∵b>0,∴b=4.2.(2018·湘潭模拟)某公司近年来特别注重创新产品的研发,为了研究年研发经费x(单位:万元)对年创新产品销售额y(单位:十万元)的影响,对近10年的研发经费xi与年创新产品销售额yi(i=1,2,…,10)的数据作了初步处理,得到如图的散点图及一些统计量的值.其中∑xi=65,∑yi=75,∑(xi-3)2=205,∑(xi-3)4=8773,∑(xi-3)2yi=2016.现拟定y关于x的回归方程为y=a(x-3)2+b.(1)求a,b的值(结果精确到0.1);(2)根据拟定的回归方程,预测当研发经费为13万元时,年创新产品销售额是多少?附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β==,α=-β.解析:(1)令t=(x-3)2,则y=at+b,=∑(xi-3)2=20.5,=∑yi=7.5,∑tiyi=∑(xi-3)2yi=2016,∑t=∑(xi-3)4=8773,a==≈0.1,b=-a=7.5-0.10×20.5=5.45≈5.5.(2)由(1)知,y关于x的回归方程为y=0.1(x-3)2+5.5,当x=13时,y=0.1×(13-3)2+5.5=15.5(十万元)=155万元,故可预测当研发经费为13万元时,年创新产品销售额是155万元.3.(2018·湘潭模拟)如图,三棱锥BACD的三条侧棱两两垂直,BC=BD=2,E,F分别是棱CD,AD的中点.(1)证明:平面ABE⊥平面ACD;(2)若四面体ABEG的体积为,求线段AE的长.解析:(1)证明:因为BC=BD,E是棱CD的中点,所以BE⊥CD.又三棱锥BACD的三条侧棱两两垂直,且BC∩BD=B,所以AB⊥平面BCD,则AB⊥CD.因为AB∩BE=B,所以CD⊥平面ABE,又CD⊂平面ACD,所以平面ABE⊥平面ACD.(2)取BD的中点G,连接EG,则EG∥BC.易证BC⊥平面ABD,从而EG⊥平面ABD,所以四面体ABEG的体积为××AB×BD×EG==,则AB=3,在Rt△ABE中,BE=,AE==.4.请在下面两题中任选一题作答(选修4-4:坐标系与参数方程)(2018·临沂模拟)在平面直角坐标系中,以原点为极点,以x轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线C1的极坐标方程为:ρ=2cosθ.(1)若曲线C2参数方程为:(α为参数),求曲线C1的直角坐标方程和曲线C2的普通方程;(2)若曲线C2参数方程为(t为参数),A(0,1),且曲线C1与曲线C2交点分别为P,Q,求+的取值范围.解析:(1)∵ρ=2cosθ,∴ρ2=2ρcosθ,又∵ρ2=x2+y2,ρcosθ=x,∴曲线C1的直角坐标方程为:x2+y2-2x=0.曲线C2的普通方程为:x2+(y-1)2=t2.(2)将C2的参数方程:(t为参数)代入C1的方程:x2+y2-2x=0得:t2+(2sinα-2cosα)t+1=0.∵Δ=(2sinα-2cosα)2-4=8sin2-4>0,∴∈,∴sin∈∪.t1+t2=-(2sinα-2cosα)=-2sin,t1·t2=1>0.∵t1·t2=1>0,∴t1,t2同号,∴|t1|+|t2|=|t1+t2|.由t的几何意义可得:+=+====2∈(2,2],∴+∈(2,2].(选修4-5:不等式选讲)(2018·临沂模拟)已知函数f(x)=|2x+b|+|2x-b|.(1)若b=1,解不等式f(x)>4,(2)若不等式f(a)>|b+1|对任意的实数a恒成立,求b的取值范围.解析:(1)b=1时,f(x)=|2x+1|+|2x-1|>4,⇒x>1或⇒x<-1或⇒x∈∅.所以解集为(-∞,-1)∪(1,+∞).(2)f(a)=|2a+b|+|2a-b|=|2a+b|+|b-2a|≥|(2a+b)+(b-2a)|=|2b|.当且仅当(2a+b)·(b-2a)≥0时(f(a))min=|2b|,所以|2b|>|b+1|,所以(2b)2>(b+1)2,所以(3b+1)(b-1)>0.所以b的取值范围为∪(1,+∞).