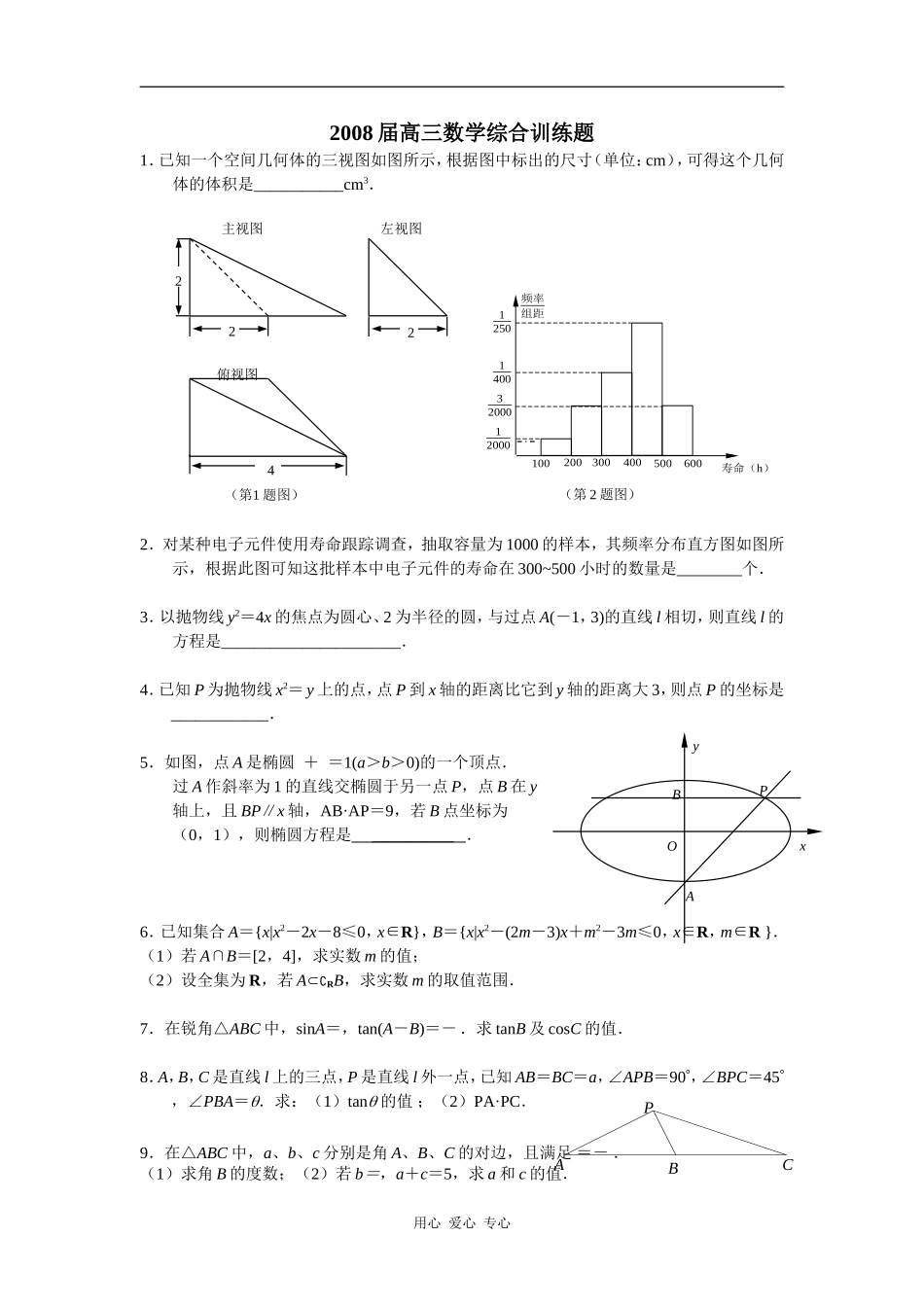
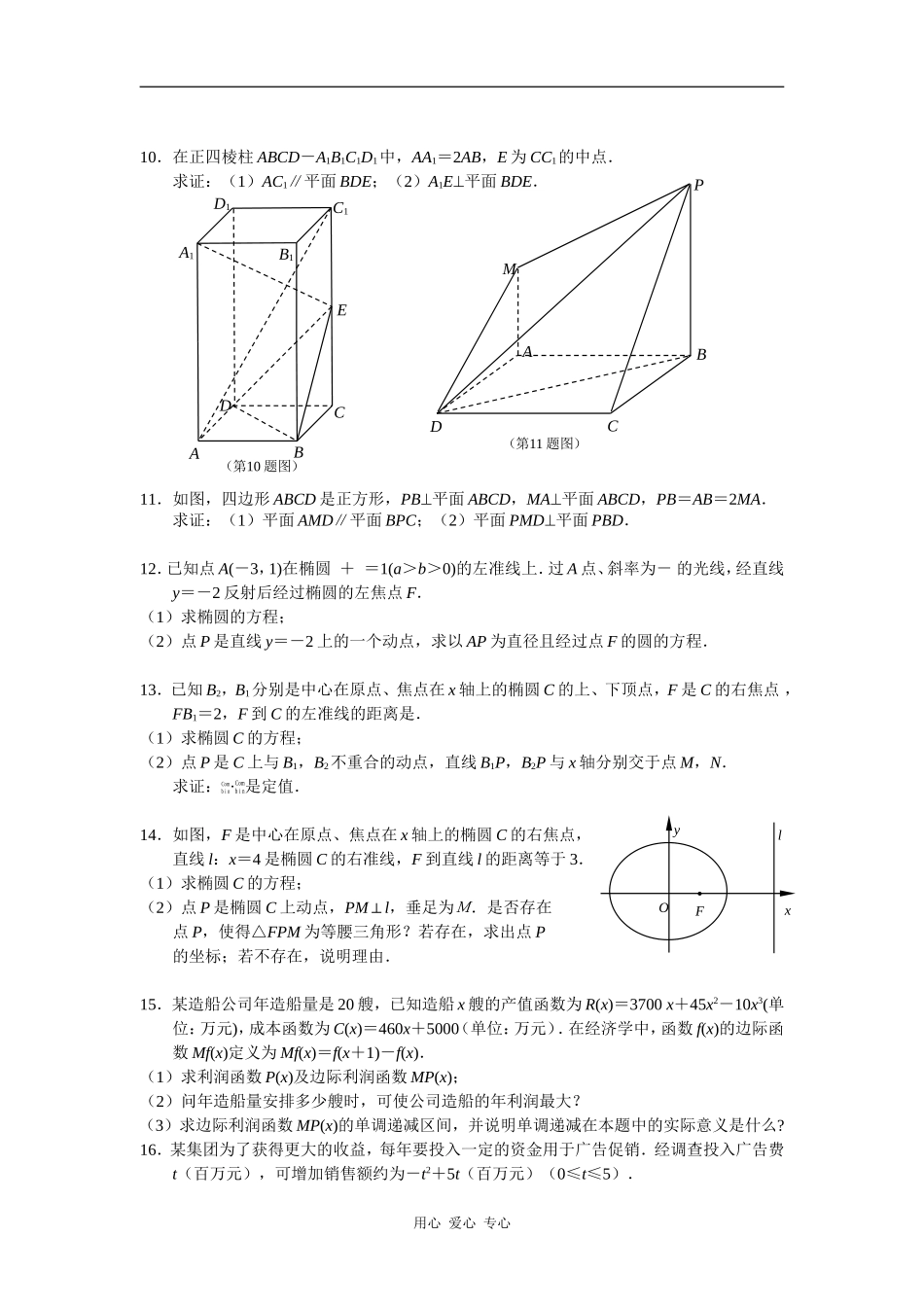
2008届高三数学综合训练题1.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是___________cm3.2.对某种电子元件使用寿命跟踪调查,抽取容量为1000的样本,其频率分布直方图如图所示,根据此图可知这批样本中电子元件的寿命在300~500小时的数量是________个.3.以抛物线y2=4x的焦点为圆心、2为半径的圆,与过点A(-1,3)的直线l相切,则直线l的方程是______________________.4.已知P为抛物线x2=y上的点,点P到x轴的距离比它到y轴的距离大3,则点P的坐标是____________.5.如图,点A是椭圆+=1(a>b>0)的一个顶点.过A作斜率为1的直线交椭圆于另一点P,点B在y轴上,且BP∥x轴,AB·AP=9,若B点坐标为(0,1),则椭圆方程是__________.6.已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R}.(1)若A∩B=[2,4],求实数m的值;(2)设全集为R,若A∁RB,求实数m的取值范围.7.在锐角△ABC中,sinA=,tan(A-B)=-.求tanB及cosC的值.8.A,B,C是直线l上的三点,P是直线l外一点,已知AB=BC=a,∠APB=90,∠BPC=45,∠PBA=.求:(1)tan的值;(2)PA·PC.9.在△ABC中,a、b、c分别是角A、B、C的对边,且满足=-.(1)求角B的度数;(2)若b=,a+c=5,求a和c的值.用心爱心专心PABCxyOAPB22主视图24左视图俯视图(第1题图)寿命(h)频率组距125032000120001400600100200300400500(第2题图)10.在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.求证:(1)AC1∥平面BDE;(2)A1E平面BDE.11.如图,四边形ABCD是正方形,PB平面ABCD,MA平面ABCD,PB=AB=2MA.求证:(1)平面AMD∥平面BPC;(2)平面PMD平面PBD.12.已知点A(-3,1)在椭圆+=1(a>b>0)的左准线上.过A点、斜率为-的光线,经直线y=-2反射后经过椭圆的左焦点F.(1)求椭圆的方程;(2)点P是直线y=-2上的一个动点,求以AP为直径且经过点F的圆的方程.13.已知B2,B1分别是中心在原点、焦点在x轴上的椭圆C的上、下顶点,F是C的右焦点,FB1=2,F到C的左准线的距离是.(1)求椭圆C的方程;(2)点P是C上与B1,B2不重合的动点,直线B1P,B2P与x轴分别交于点M,N.求证:Combin·Combin是定值.14.如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.(1)求椭圆C的方程;(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.15.某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3700x+45x2-10x3(单位:万元),成本函数为C(x)=460x+5000(单位:万元).在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).(1)求利润函数P(x)及边际利润函数MP(x);(2)问年造船量安排多少艘时,可使公司造船的年利润最大?(3)求边际利润函数MP(x)的单调递减区间,并说明单调递减在本题中的实际意义是什么?16.某集团为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查投入广告费t(百万元),可增加销售额约为-t2+5t(百万元)(0≤t≤5).用心爱心专心xyOlFEABCDA1B1C1D1(第10题图)ABCDPM(第11题图)(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?(注:收益=销售额-投放).17.要设计一容积为V的下端为圆柱形、上端为半球形的密闭储油罐,已知圆柱侧面的单位面积造价是下底面的单位面积造价的一半,而顶部半球面的单位面积造价又是圆柱侧面的单位面积的造价的一半,问储油罐的下部圆柱的底面半径R为何值时造价最低?18.已知函数f(x)=x3-3ax(a∈R).(1)如果a=l,求f(x)的极小值;(2)如果a≥l,g(x)=|f(x)|,x[∈-l,1],求g(x)的...